【算法】计算机图形学的一些经典小题：判断点在多边形内，随机生成三角形内的点，判断两个矩形是否相交等

前几天面试的时候被问到了，如何随机在三角形内生成点，我按照我的想法回答了一遍，但觉得回答的不够好。最后面试官说了一个最优的方法。觉得不错，顺带总结一下最近看到的一些关于计算机图形学方面的经典小题，知乎上看到的还有Leetcode上的

1.判断一个点是否在多边形内

首先先说一下输入的内容，多边形的顶点是一个数组输入进来，其中每个相邻点之间对应着多边形上有边相连

POINT p1 = ptPolygon[i];
POINT p2 = ptPolygon[(i + 1) % nCount];

即上面两个点之间存在边相连

判断是否在凸多边形内部

这个方法我记得是在编程之美上看到的，即计算该点与多边形点之间向量的叉积，如果叉积同向则说明在内部，如果有反向则说明在外部。

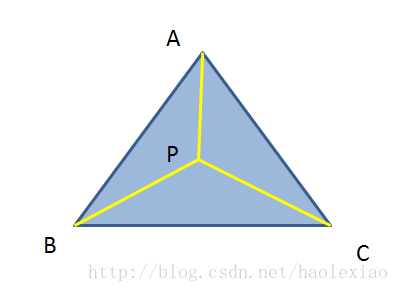
比如上面这个图，分别计算 PA→,PB→ 的叉积 PB,PC→ 的叉积 PC→,PA→ 的叉积
如果其都是同向的，则说明其在内部，如果不是同向的，则说明在外部。
这个算法复杂度是 O(n) 的， n 是多边的顶点数

判断是否在任意多边形内部

一个经典的算法是射线法

• 从该点P出发向任意方向射出一条射线, 如果与多边形的边相交的数量为奇数个,则说明其在内部,如果相交个数为偶数个则在内部

• 一般为了计算方便就选择从P点向 x 轴向右方向上的射线，而判断相交只用求出交点的横坐标看起是否大于P.x的坐标就好

  具体的算法实现见这个判断点是否在多边形内的算法和C语言程序

2.随机生成三角形内的点

这个是被面试官问到的题目，我的做法是先将三角形的外围用一个矩形给括起来，然后对矩形内的点进行随机采样，采样出来的点用上面1中的方法判断是否在三角形内。如果不在则继续采样。
面试官对此不是很满意，后来我想出来可以通过左边轴变换的方式进行，但是回答的也不好
最后面试官说了自己的方法：

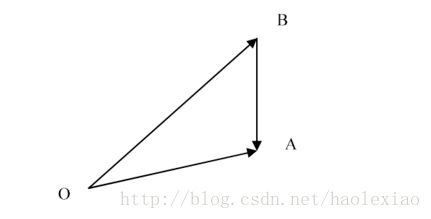
网上找了一个图将就着看吧
其实这个方法也是坐标轴转换的思想，我之前想到的已经比较接近了，只不过没有往向量这块去考虑。
即由之前的 xy 坐标系转换为以三角形的两条边为基底的坐标系,如上图所示转换为 OA→,OB→ 作为坐标的表示,所以 OP→=tOA→+kOB→ 如果 0<t,k<1 的话其在 OA→,OB→ 组成的平行四边形内，判断P点是否在三角形内只用判断 t+k<1 即可，如果在三角形内则采样成功，如果不在三角形内则可以再次采样，还有更精妙的算法，就是将超出的点重新映射到这个三角形内即可将其变为 OP→=(1−t)OA→+(1−k)OB→ 即可，推导非常简单，可以自己尝试一下，思路是如果超出三角形的话，可以将其看成O点对应平行四边形的顶点C点进行生成的落在 ΔOAB 内的的点，而C点本身可以看成 OA→+OB→ 得到

一个非常容易的易错点

这道题一个非常经典的易错思路是：比如上面的方法先随机生成t，然后再在(0,1-t)的区间内生成k点。
因为这种不随机：
比如假设t生成的结果非常接近于1，如果按照原始的方法则会出现大概率出现采样超过原来三角形的情况，而在这种采样的方式之下，必然会采样成功。

3.判断一个圆形和矩形是否相交

这道题是今天知乎上看到的：
怎样判断平面上一个矩形和一个圆形是否有重叠？
具体的算法也非常简单易懂，但是非常的巧妙。
我总结一下巧妙的地方在于：

1. 先通过一个变换，将圆形变到了矩形的右上角，
2. 通过向量，外加取最大值来巧妙的求得了圆形到矩形的最短距离【所以这个题目的简化版本可以用来求解圆形到矩形的最短距离】

4.判断两个矩形是否相交并求相交部分面积

Leetcode上有这道题：
223. Rectangle Area
我一开始的思路是，类比与上面那道题，将第二个矩形换到第一个矩形右上角，然后判断以第一个矩形右顶点为坐标原点时，第二个矩形的左下角是否落在了第三象限。这样用来判断是否相交还是不错的，但是求面积就不行了，比如如下的图

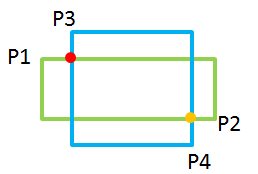
然后翻Leecode的discuss，底下最高票答案给的方法一时没看明白

int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
    int left = max(A,E), right = max(min(C,G), left);
    int bottom = max(B,F), top = max(min(D,H), bottom);
    return (C-A)*(D-B) - (right-left)*(top-bottom) + (G-E)*(H-F);
}

后来查到了另外一个人的博客，我觉得它讲的挺明白的： 判断两矩形是否相交
这道题本质上相当于求两个矩形相交区域的横纵坐标

int left = max(A,E);
int bottom = max(B,F);

这个是求得相交区域左下角的坐标的。如果不相交也是没有问题的
这个可以这么看，即两个矩形的左边和下面两条边做直线延长，然后得到的相交区域一定是一个矩形，然后上面求得的坐标就是这个矩形的右上角
同理，右边和上面四条边所在直线相交点的左下角为：

int right = min(C,G);
int top = min(D,H);

在判断一下以上两个坐标点的相对位置，如果第一个在第二个左下角的话，则能够构成矩形，如果不是这种情况则不能构成矩形。