数据结构--柯朵莉树
目录
- 一道例题,先跳过qwq
- 从这里开始看ovo
- 目录0.0
- 1.什么是柯朵莉树
- 2.柯朵莉树的初始化
- 3.柯朵莉树的核心操作 split()
- 4. assign()操作
- 5. 其他操作
- 6. 到这就结束了,放上全部的代码qwq
一道例题,先跳过qwq
题目链接
题目描述
lxhgww最近收到了一个01序列,序列里面包含了n个数,这些数要么是0,要么是1,现在对于这个序列有五种变换操作和询问操作:
0 a b 把[a, b]区间内的所有数全变成0
1 a b 把[a, b]区间内的所有数全变成1
2 a b 把[a,b]区间内的所有数全部取反,也就是说把所有的0变成1,把所有的1变成0
3 a b 询问[a, b]区间内总共有多少个1
4 a b 询问[a, b]区间内最多有多少个连续的1
对于每一种询问操作,lxhgww都需要给出回答,聪明的程序员们,你们能帮助他吗?
输入格式
输入数据第一行包括2个数,n和m,分别表示序列的长度和操作数目
第二行包括n个数,表示序列的初始状态
接下来m行,每行3个数,op, a, b,(0<=op<=4,0<=a<=b 输出格式 输入输出样例 对于100%的数据,1<=n, m<=100000 之前闲来无事逛OI-wiki的时候发现了这个东西 OI和ACM有一类题,是维护区间的数值 这种题一般会给你一个1e5的数组,之后会进行一些操作,改变特定区间内的值,之后询问你区间最大值/最小值 如果你直接使用数组存,用循环来改变区间值,再用循环来统计,那肯定会TLE得欲仙欲死w 这个时候就可以使用线段树了 线段树详解 好了,回到正题,如果区间操作中有大量的区间赋值,并且数据随机,那么,就可以用柯朵莉树代替线段树,写过线段树的应该都会对它的代码量,以及找bug的过程印象深刻,而柯朵莉树的代码量比线段树少很多! 而这个数据结构的来源 在这之前,可以先去看一下例题了OVO 欢迎回来awa 为了保证区间操作以及查询不会超时,同时为了写起来方便,我们选择了使用STL中的set容器来存储内容 set内部是用红黑树实现的,同时操作起来也非常简单,符合我们暴力的思想(手动滑稽) 对于set中每一个节点,我们都要保存一个区间的值,所以我们这样定义 节点中,在l到r这个区间的值为v(以下称node为区间节点) 因为set是用红黑树实现的,所以它插入数据时内部会根据小于号来进行从小到大排序,上面这部分就是重载小于号运算符 上面这部分是c++中的构造函数,在c语言中,我们想定义一个结构体变量,并对结构体变量中的各个子变量赋值时,我们要用变量名.变量名的方式,一个一个赋值,而如果我们使用这个构造函数,我们可以直接给结构体中的各个变量赋值,具体用法下面再讲 ovo 录入区间节点时,直接插入单个区间节点就OK 根据上面的知识,我们知道,set里每个区间节点存储的是区间的和(可能你会要问录入区间节点的时候不是一个一个存的吗,不要急,往下看w) 我们逐条来看 lower_bound会返回一个下标,注意这里,不要写成下面这样 这相当于把set中,这段区间节点的区间值提取出来,存到一个数组里,再进行二分查找,set想要提取一个元素的复杂度是logn,所以如果这么写,复杂度就会变成O(nlogn) 如果指针没有指向end(),并且当前节点的左端点 l (左边这个是小写L,这个字体看的好难受qwq),正好是我们想要split的位置,我们直接把当前的指针返回即可 , 否则 it-1 对于it指向end()的情况,通过这个操作,可以让它指向有区间节点的位置,而对于其他情况,当前的区间节点的左端点不是我们想要的,那么根据lower_bound()的性质(返回第一个不小于要找的元素的位置),它返回的区间节点的左端点,一定是大于我们想要split的左端点的,所以我们要找的左端点,在它前面的区间节点里。 所以我们要把这个区间节点拆开,拆成两个节点 register关键字是把它后面申明的变量放入CPU的寄存器中,以在重复使用时达到更快的速度,一般c++中,会自动把for循环中的i放入CPU寄存器,让for循环跑的更快 这里就用到了前面的构造函数,我们如果按照c语言中给结构体赋值的方法,写起来很麻烦,速度还会慢一些 assign()操作,是对区间进行赋值 我们还是逐行来看 我们要对[l, r]这个区间进行赋值,那么之前存储的这段区间的值都没有用了,所以我们要把包含这段区间的节点删掉 set的erase()函数可以传两个指针,表示对这一段区间进行删除操作,不过,它是左闭右开区间,所以,我们要split(r + 1),split(l),这个顺序不能反过来,要先split右边,否则处理边界情况的时候会报错qwq 之后,把要赋值的区间,构造一个node插入进set里就OK了! 这一部分就非常简单了,因为全是暴力操作的 我先给你们举个例子,求区间最大值 整体代码
对于每一个询问操作,输出一行,包括1个数,表示其对应的答案
输入 #1
10 10
0 0 0 1 1 0 1 0 1 1
1 0 2
3 0 5
2 2 2
4 0 4
0 3 6
2 3 7
4 2 8
1 0 5
0 5 6
3 3 9
输出 #1
5
2
6
5
说明/提示
对于30%的数据,1<=n, m<=1000从这里开始看ovo
用来在某些条件下代替线段树的暴力型数据结构
正好记录一下
看此文最好有线段树基础ovo目录0.0
1.什么是柯朵莉树
如果你想实际操作一下线段树的话,可以试试这个
不过这毕竟是一种暴力的手段,对于OI来说可以骗分,对于ACM来说……
是CF896C这道题的出题人,因此,这个数据结构又被称为ODT(old driver tree)(老司机树)
ODT对ODT的介绍与证明(2.柯朵莉树的初始化
struct node {
int l, r;
mutable int v;
node(int _l, int _r = -1, int _v = 0) : l(_l), r(_r), v(_v) {}
bool operator<(const node &o) const {
return l < o.l;
}
};
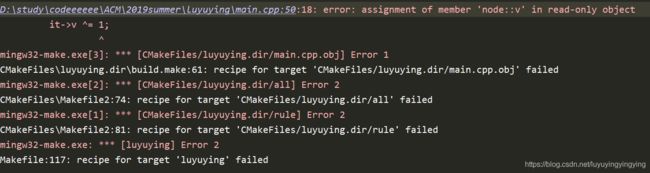
mutable与const相对,表示这个变量永远是可变的,对于这个关键字,百度搜到的说法与这个用法关系不大,我感觉问题出在set,访问set里的变量通过迭代器,对于迭代器来说,node里的变量是只读的
这是不加mutable后报的错
bool operator<(const node &o) const {
return l < o.l;
}
node(int _l, int _r = -1, int _v = 0) : l(_l), r(_r), v(_v) {}
在set最末尾还要插一个区间节点,为了后面的操作 for (int i = 1; i <= n; i++) {
cin >> t;
s.insert(node(i, i, t));
}
s.insert(node(n + 1, n + 1, 0));
3.柯朵莉树的核心操作 split()
如果set里有这样一个区间节点,l=1,r=10,v=10

我们要改变1到5的值为5,这时候就需要从6这分开,至于为什么要从6分开,下面assign()操作里会讲,别急qwq

下面是代码#define IT set
inline关键字是给编译器一个建议,让编译器把这个函数变为内联函数……
这些话可以无视,知道它能加快运行速度就可以了= =register IT it = lower_bound(s.begin(), s.end(), node(pos));
所以我们要直接调用set里的lower_bound函数。if (it != s.end() && it->l == pos)return it;
register int l = it->l, r = it->r, v = it->v;//把当前区间节点的各个值记录下来
s.erase(it);//删除当前区间节点
s.insert(node(l, pos - 1, v));//把l到pos-1插进set
return s.insert(node(pos, r, v)).first;//把pos到r这个区间节点插进去,并且返回插进去的节点的指针
先留着,等我知道的更多了之后再回来补充4. assign()操作
inline void assign(int l, int r, int v) {
register IT itr = split(r + 1), itl = split(l);
s.erase(itl, itr);
s.insert(node(l, r, v));
return;
}
register IT itr = split(r + 1), itl = split(l);
s.erase(itl, itr);
5. 其他操作
区间求和就把这个区间的元素都取出来,一个一个加起来求和
区间求第k大值,就把这个区间的元素都取出来,排个序,就能得出来第k大了
是不是有种无力吐槽的感觉-_-||inline int longsum(int l, int r) {
register IT itr = split(r + 1), itl = split(l);
int mx = 0, t = 0;
for (; itl != itr; itl++) {
if (itl->v == 1) {
t += itl->r - itl->l + 1;
mx = max(mx, t);
} else {
t = 0;
}
}
return mx;
}
6. 到这就结束了,放上全部的代码qwq
#include