计算几何基础知识学习整理

今天终于开始接触了一下计算几何。。这里很多基础题都有板子。。先简单介绍一下计算几何基础概念和知识：

矢量加减法：设二维矢量P = ( x1, y1 )，Q = ( x2 , y2 )，则矢量加法定义为： P + Q = ( x1 + x2 , y1 + y2 )，

同样的，矢量减法定义为： P - Q = ( x1 - x2 , y1 - y2 )。

显然有性质 P + Q = Q + P，P - Q = - ( Q - P )。 

矢量叉积：计算矢量叉积是与直线和线段相关算法的核心部分。

设矢量P = ( x1, y1 )，Q = ( x2, y2 )，则矢量叉积定义为由(0,0)、p1、p2和p1+p2所组成的平行四边形的带符号的面积，

即：P × Q = x1*y2 - x2*y1，

其结果是一个标量。显然有性质 P × Q = - ( Q × P ) 和 P × ( - Q ) = - ( P × Q )。

一般在不加说明的情况下，本文下述算法中所有的点都看作矢量，两点的加减法就是矢量相加减，而点的乘法则看作矢量叉积。

【叉积的一个非常重要性质是可以通过它的符号判断两矢量相互之间的顺逆时针关系】 
1）若 P × Q > 0 , 则P在Q的顺时针方向。 
2）若 P × Q < 0 , 则P在Q的逆时针方向。 
3）若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向。  

以上资料来自于：https://blog.csdn.net/reverie_mjp/article/details/51340387

判断点是否在线段上：设点为Q，线段为P1P2 ，判断点Q在该线段上的依据是：( Q - P1 ) × ( P2 - P1 ) = 0 且 Q 在以 P1，P2为对角顶点的矩形内。前者保证Q点在直线P1P2上，后者是保证Q点不在线段P1P2的延长线或反向延长线上，对于这一步骤的判断可以用以下过程实现： 

/*计算向量p1p2与向量p1p3的叉积，若p1p3在p1p2的逆时针方向，则返回>0，顺时针方向返回<0*/
int mul(Point p1,Point p2,Point p3)
{
    return (p2.x-p1.x)*(p3.y-p1.y)-(p2.y-p1.y)*(p3.x-p1.x);
}

之后就是判断线段相交了

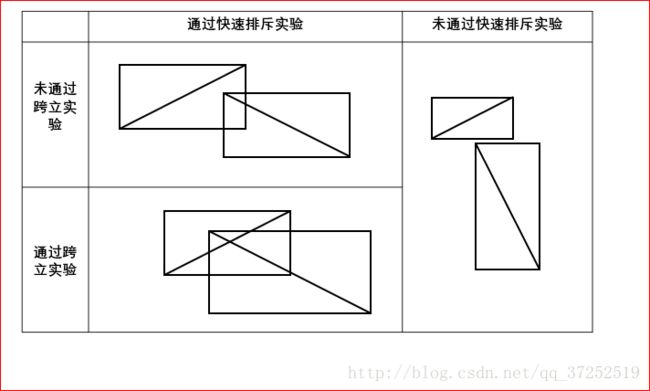
1.快速排斥实验。

 设以线段A1A2为对角线的矩形为R，设以对角线B1B2为对角线的矩形为T，如果R和T不想交，显然这两个线段不相交。

判断矩形相交，只需判断某一矩形是否有顶点在另一矩形内。

2. 跨立实验。

 设向量P1=向量OA1，P2=向量OA2，Q1=向量OB1,Q2=向量OB2.

若线段A1A2跨立线段B1B2，则向量（P1-Q1）和（P2-Q1)位于向量（Q2-Q1）的两侧，

（（P1-Q1) x (Q2-Q1) ) · （（P2-P1) x (Q2-Q1) ) < 0

当 （P1-Q1) x (Q2-Q1) =0 时，说明（P1-Q1) 和 (Q2-Q1) 共线，但是因为通过了快速排序实验，所以点A1一定在B1B2上。

同理，（P2-P1) x (Q2-Q1) =0 时，所以点A2一定在B1B2上。

所以判断线段A1A2跨立线段B1B2的依据是

（ ( P1-Q1 ) x ( Q2 - Q1 ) ）· （（ Q1 - P2 ）x ( Q2 - Q1 ) ）>=0

同理，判断线段B1B2跨立A1A2线段的依据是

 ( ( Q1-P1) x ( P2 - P1 ) )· ( ( P1 -Q2 ) x ( Q2 - Q1 ） ）>=0

这张图片非常棒 以上资料来自：https://blog.csdn.net/qq_37252519/article/details/79142029

有了这些知识可以适当接触一下计算几何水题了