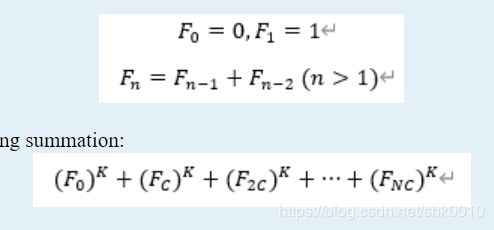2020 Multi-University Training Contest #1 1005 Fibonacci Sum

2020 Multi-University Training Contest #1 1005 Fibonacci Sum

题意

hdu 6755 Fibonacci Sum

求后面的值。

题解

根据斐波那契通项式 $F(n)=\frac{1}{\sqrt{5}}(a^n-b^n)$
其中$a=\frac{1+\sqrt{5}}{2}$,$b=\frac{1-\sqrt{5}}{2}$

带入式子可得$S(n)={\frac{1}{\sqrt{5}}}^k{\sum }_{n=0}^N(a^{nc}-b^{nc}{)}^k$
二项式展开得$S(n)={\frac{1}{\sqrt{5}}}^k{\sum }_{n=0}^N{\sum }_{i=0}^k{C}_k^i{a}^{nc(k-i)}{b}^{nci}(-1{)}^i$
去掉n可得$S(n)={\frac{1}{\sqrt{5}}}^k{\sum }_{i=0}^k(-1{)}^i{C}_k^i\frac{a^{(n+1)c(k-i)}{b}^{(n+1)ci}-1}{a^{c(k-i)}{b}^{ci}-1}$

这个时候用二次剩余求出$\sqrt{5}$的mod意义下的值然后求出a，b就已经可以求解了，但是阴险的朝鲜人卡了常数……4个logn的快速幂过不去，意味着要大量优化。
根据通项式可得知分母每次更改的值为${\frac{b}{a}}^c$,分子每次更改的值为${\frac{b}{a}}^{nc}$分子起始项为$a^{ck(n+1)}$ ,而且$n+1$的指数也太大了，所以需要对其欧拉降幂，变为(n+1)%(mod-1) (mod为素数)。分母的起始项为$a^{ck}$
其他细节看代码吧（比如说很多long long）

代码

#include
#define ll long long
#define INF 0x3f3f3f3f
#define LLINF 0x3f3f3f3f3f3f3f3f
#define pii pair
#define vi vector
#define SZ(x) (int)x.size()
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define mod 1000000009
using namespace std;
const int N = 1e5 + 5;
const int v5 = 383008016;
const int v51 = 276601605;
const int a = 691504013;
const int ad = 691504012;//a^-1
const int b = 308495997;
inline int powmod(int a, ll b) {
    int res = 1;
    a = a % mod;
    while(b) {
        if(b & 1) res = (ll)res * a % mod;
        a = (ll) a * a % mod;
        b >>= 1;
    }
    return res;
}
ll fac[N], inv[N];
void init() {
    fac[0] = 1;
    for(int i = 1; i < N; i++) {
        fac[i] = fac[i - 1] * i % mod;
    }
    inv[N - 1] = powmod(fac[N - 1], mod - 2);
    for(int i = N - 2; i >= 0; i--) {
        inv[i] = inv[i + 1] * (i + 1) % mod;
    }
}
inline int C(int n, int m) {
    if(m > n) {
        return 0;
    }
    if(m == 0) {
        return 1;
    }
    return fac[n] * inv[m] % mod * inv[n - m] % mod;
}
int main(){
   init();
   
   int t;
   scanf("%d", &t);
   while(t--) {
        ll n, c;
		int k;
        scanf("%lld%lld%d", &n, &c, &k);
        int sum = 0;
		int add = powmod((ll)ad * b % mod, c);//增加 
		int n1 = (n + 1) % (mod - 1);//降幂 
		int n0 = (n + 1) % mod;
		int q1 = powmod(a, c);
		int  q = powmod(q1, k);
		int st = powmod(q, n1);
		int d1 = powmod(add, n1);
		for(int i = 0; i <= k; i++) {
			int cnt = C(k, i);
			if(i & 1) cnt = mod - cnt;
			if(q == 1) {
				sum= ((ll)sum + (ll)n0 * cnt % mod) % mod;
			}
			else 
				sum = ((ll)sum + (ll)(st - 1 + mod) % mod * powmod(q - 1, mod - 2) % mod * cnt % mod) % mod;
			q = (ll)q * add % mod;
			st = (ll)st * d1 % mod;
		}
        printf("%d\n", (ll)sum * powmod(v51, k) % mod);
   }
}```