《深度学习》第二章线性代数
第二章 线性代数
目录
文章目录
- 第二章 线性代数
- 目录
- 线性代数的表示
- 矩阵的转置
- 矩阵相乘
- 向量的线性相关性与矩阵的秩
- 单位矩阵与逆矩阵
- 向量的范数
- 特征值分解
线性代数的表示
-
标量(Scalars)
单个数值:整数5、实数0.5、有理数1/3等
用小写字母表示,如 a, n, x -
向量(Vectors)
一维数组,无特别说明,即指列向量
加粗小写,如
x = [ x 1 x 2 . . . x n ] = ( x 1 , x 2 , . . . , x n ) T \mathbf{x}= \begin{bmatrix} x_1 \\ x_2 \\ ...\\ x_n \end{bmatrix} = \begin{pmatrix} x_1, x_2, ..., x_n \end{pmatrix}^T x=⎣⎢⎢⎡x1x2...xn⎦⎥⎥⎤=(x1,x2,...,xn)T -
矩阵(Matrix)
二维数组
大写字母表示 A m × n A_{m \times n} Am×n 或 A ∈ R m × n A \in R^{m\times n} A∈Rm×n
向量可视为 m × 1 m \times 1 m×1 的矩阵 -
张量(Tensor)
数组的扩展
矩阵的转置
- 定义:行、列坐标互换,行变列,列变行
( A T ) i , j = A j , i (A^T)_{i,j} = A_{j,i} (AT)i,j=Aj,i
如:
A 3 × 2 = [ A 1 , 1 A 1 , 2 A 2 , 1 A 2 , 2 A 3 , 1 A 3 , 2 ] 则 A 2 × 3 T = [ A 1 , 1 A 2 , 1 A 3 , 1 A 1 , 2 A 2 , 2 A 3 , 2 ] A_{3 \times 2} = \begin{bmatrix} A_{1,1} & A_{1,2} \\ A_{2,1} & A_{2,2} \\ A_{3,1} & A_{3,2} \\ \end{bmatrix} 则 \\ A^T_{2 \times 3} = \begin{bmatrix} A_{1,1} & A_{2,1} & A_{3,1} \\ A_{1,2} & A_{2,2} & A_{3,2} \\ \end{bmatrix} A3×2=⎣⎡A1,1A2,1A3,1A1,2A2,2A3,2⎦⎤则A2×3T=[A1,1A1,2A2,1A2,2A3,1A3,2]
矩阵的转置有性质:
( A B ) T = B T A T (AB)^T=B^{T}A^T (AB)T=BTAT
矩阵相乘
- 第一种理解:元素为列乘以行
有矩阵 A m × n A_{m \times n} Am×n B l × k B_{l \times k} Bl×k 若 n = l n=l n=l, A B AB AB 存在
矩阵 A A A B B B 相乘,其元素由下式计算
( A B ) i , j = ∑ k A i , k B k , j (AB)_{i,j}=\sum_k A_{i,k}B_{k,j} (AB)i,j=k∑Ai,kBk,j
如
A B = [ 1 2 3 4 5 6 ] [ 1 4 2 5 3 6 ] = [ ( 1 , 2 , 3 ) ( 1 , 2 , 3 ) T ( 1 , 2 , 3 ) ( 4 , 5 , 6 ) T ( 4 , 5 , 6 ) ( 1 , 2 , 3 ) T ( 4 , 5 , 6 ) ( 4 , 5 , 6 ) T ] AB= \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix} \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \\ \end{bmatrix}= \begin{bmatrix} (1,2,3) (1,2,3)^T & (1,2,3) (4,5,6)^T \\ (4,5,6) (1,2,3)^T & (4,5,6) (4,5,6)^T \\ \end{bmatrix} AB=[142536]⎣⎡123456⎦⎤=[(1,2,3)(1,2,3)T(4,5,6)(1,2,3)T(1,2,3)(4,5,6)T(4,5,6)(4,5,6)T]
另一种理解:行乘以列的各矩阵相加
A B = [ 1 2 3 4 5 6 ] [ 1 4 2 5 3 6 ] = ( 1 , 4 ) ( 1 , 4 ) T + ( 2 , 5 ) ( 2 , 5 ) T + ( 3 , 6 ) ( 3 , 6 ) T = [ 1 4 4 16 ] + [ 4 10 10 25 ] + [ 9 18 18 36 ] AB= \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix} \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \\ \end{bmatrix}= (1,4) (1,4)^T+(2,5) (2,5)^T+(3,6) (3,6)^T \\ = \begin{bmatrix} 1 & 4 \\ 4 & 16 \end{bmatrix} + \begin{bmatrix} 4 & 10 \\10 & 25 \end{bmatrix} + \begin{bmatrix} 9 & 18 \\18 & 36 \end{bmatrix} AB=[142536]⎣⎡123456⎦⎤=(1,4)(1,4)T+(2,5)(2,5)T+(3,6)(3,6)T=[14416]+[4101025]+[9181836]
向量的线性相关性与矩阵的秩
-
定义
对向量组 x 1 , x 2 , . . . , x s ( s ≥ 1 ) \mathbf x_1, \mathbf x_2, ..., \mathbf x_s (s \ge 1) x1,x2,...,xs(s≥1) 若存在一组不全为0的数
k 1 , . . . , k s k_1, ..., k_s k1,...,ks
使得
k 1 x 1 + . . . + k s x s = 0 k_1\mathbf x_1+...+k_s\mathbf x_s=0 k1x1+...+ksxs=0
则称该向量组线性相关,反之,则线性无关
线性无关的充要条件:其中任何一个向量不能由其余向量线性表出 -
极大线性无关组
对于一个向量组$\mathbf x_1, …, \mathbf x_s $,若存在一个部分组,满足:
-
这个部分组线性无关
-
如果从向量组的其余部分中任取一个添加进去,则到的新部分组都线性相关,则这个部分组称为向量组$\mathbf x_1, …, \mathbf x_s $的极大线性无关组
向量组与它的任意一个极大线性无关组等价(等价——互可线性表出)
不含零向量的向量组如果线性相关,则它的极大线性无关组肯定不止一个
-
向量组的秩
向量组的一个极大线性无关组所含的向量的个数,记为 r a n k { x 1 , . . . , x s } rank\{\mathbf x_1, ..., \mathbf x_s\} rank{x1,...,xs} -
矩阵的秩
矩阵的列微量组的秩称为 A A A 的列秩, A A A 的行向量组的秩称为 A A A 的行秩
任一矩阵的行秩等于其列秩,统称为矩阵 A A A 的秩,记作 r a n k ( A ) rank(A) rank(A)
单位矩阵与逆矩阵
-
方阵:行数等于列数 A n × n A_{n \times n} An×n
-
对角矩阵:对于一个方阵,对角线外的元素均为零,即为对角矩阵
-
单位矩阵:对于一个对角矩阵,对角线上的元素均为1,即为单位矩阵,用 I n I_n In表示
-
逆矩阵:对方阵 A n A_n An,若存在方阵 B n B_n Bn使得 A B = B A = I AB=BA=I AB=BA=I,则 A A A为可逆矩阵, B B B与 A A A互为逆矩阵
-
矩阵可逆的等价条件
- A A A为满秩矩阵(满秩矩阵——矩阵的秩等于方阵的列数/行数)
- A A A的各列线性无关
- 非满秩方阵称为奇异矩阵
向量的范数
- 向量的大小用范数来衡量,形式上, L P L^P LP 范数定义
∣ ∣ x ∣ ∣ P = ( ∑ i ∣ x i ∣ p ) 1 p ||x||_P={(\sum_i |x_i|^p)} ^{\frac{1}{p}} ∣∣x∣∣P=(i∑∣xi∣p)p1
∣ ∣ [ 1 2 3 ] ∣ ∣ 2 = 1 2 + 2 2 + 3 2 ||\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}||_2= \sqrt {1^2+2^2+3^2} ∣∣⎣⎡123⎦⎤∣∣2=12+22+32
范数满足下列性质
- 非负性:若 x ≠ 0 \mathbf x \neq \mathbf 0 x=0,则 f ( x ) > 0 f(\mathbf x)>0 f(x)>0;$f(\mathbf x)=0 \Rightarrow \mathbf x = \mathbf 0 $
- 三角不等式(不要与凸函数性质混淆): f ( x + y ) ≤ f ( x ) + f ( y ) f(\mathbf x + \mathbf y) \le f(\mathbf x) + f(\mathbf y) f(x+y)≤f(x)+f(y)
- 齐次性: ∀ α ∈ R , f ( α x ) = ∣ α ∣ f ( x ) \forall \alpha \in \mathbb R, f(\alpha \mathbf x) = |\alpha|f(\mathbf x) ∀α∈R,f(αx)=∣α∣f(x)
- 几个常见范数
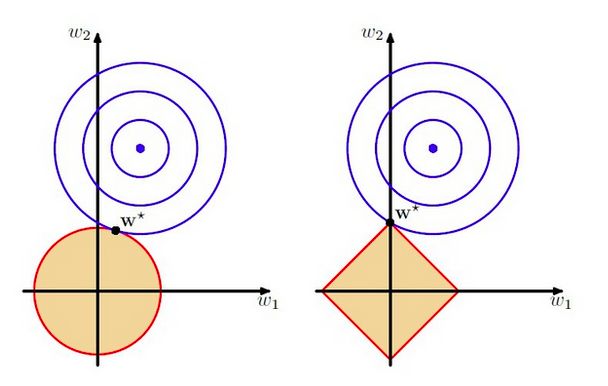
- L2范数 p = 2 p=2 p=2,欧里几得范数 L 2 = x T x L^2=x^Tx L2=xTx,机器学习中最常用
推广至矩阵Frobenius norm ∣ ∣ A ∣ ∣ F = ∑ i , j A i , j 2 ||A||_F=\sqrt {\sum_{i,j} A^2_{i,j}} ∣∣A∣∣F=∑i,jAi,j2 - L1范数 p = 1 p=1 p=1, L 1 = ∣ ∣ x ∣ ∣ 1 = ∑ i ∣ x i ∣ L^1=||\mathbf x||_1 = \sum_{i} |x_i| L1=∣∣x∣∣1=∑i∣xi∣,也较常用
- 最大范数 ∣ ∣ x ∣ ∣ ∞ = m a x i ∣ x i ∣ ||\mathbf x|| _\infty=max_i|x_i| ∣∣x∣∣∞=maxi∣xi∣
特征值分解
定义:特征向量(eigenvector)