数据结构の学习记录（二）：如何给中缀表达式加括号

对算法类的问题，最大的忌讳就是，想都不想直接写代码。

如果你的这样的程序猿，那么狠抱歉，要么就是你会花上数十倍的时间修改你的简单STUPID错误，要么就是你很短时间就能得到正确的结果，如果是这样那么恭喜你，你进化了！

说上述言论，笔者的区分点是你的目标究竟是一个码农还是一个算法工程师。两者的区别从工资上看不说你应该也懂:-)

（等不及的你可以迅速下拉到分界线以下寻找干货）

下面附上笔者的coding习惯。首先将思路以母语（中文可以但推荐英语）的形式写在草稿纸上，觉得没有问题之后，再将其用铅笔转换为代码，之后将其写在你青睐的有调试功能的开发平台上（对于笔者是Spyder，PyCharm）。如果你发现的开发平台没有调试功能，那么你需要立刻更换！对于刚写好的代码，第一步永远是调试，而不是直接运行。最后一步是不断优化，考虑所有的情况，并且优化时间复杂度和空间复杂度，永远不是喊着“哈利路亚”，然后发邮件告诉你老板任务完成了。

                                                                              第一步：将算法写在草稿纸上 

                                                                            第二步：将其转换为铅字版 代码

 

                                                               第三步：转化为实际的代码，这一步基本上是调试

---

不幸的是，笔者的博客将不会有完整代码（示范代码除外），所有代码均已上传到码云上。如果时间和精力允许的话，强烈建议你根据思路，手动写一遍，相信你会感觉到全身毛孔舒张而不是想砸电脑的快感。

术语：
运算符：进行数字运算的字符，如‘+’‘-’等
操作数：数字‘1’，‘2.5’等
栈: 存储数据的结构，讲究“先进后出”，即最先进栈的数据，最后出栈；有顺序存储和链式存储两种。

正则表达式：通常被用来检索、替换那些符合某个模式(规则)的文本。

了解了基本术语后，你知道所谓构建括号表达式，就是根据优先级和前后顺序依次加括号。如2+3*5/2，你应该得到的是2+((3*5)/2)而不是(2+3)*5/2，最外面的括号可以不加，但是不允许出现2+(3*5)/2这种不“完全”的括号表达式，尤其是对于多项的表达式更是如此。

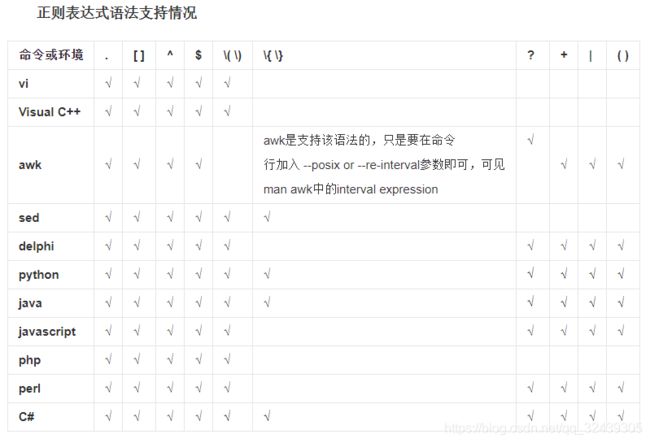
非常糟糕的是，用户的需求千变万化，因此你需要永远修改你的代码以满足用户的需要。就像这个问题一样，输入如果是整数表达式那很容易解决，但是对于小数和负数，Damn it，没有比这更恶心的了。多亏了强大的被称为“宇宙最好的语言”的Python ，它如胶水一样的灵活，容易上手，提供强大的库。好了，废话不多说了，你已经猜到我要说什么了。那就是正则表达式（REGEX）。如果你不熟悉的话，在我之前的博文有讲解，下面一张表格记录了各种语言对正则表达式的支持情况。

可见Java, Python, Perl,C#是完全支持正则表达式的。我们希望构建一个expression_spliter函数来将输入的字符，转换为分割之后的列表。举个例子input：‘4.2/(-3.5*+2+2^-2.2/4*5%6)+3-(-4.5)’ ，output：[' 4.2', '/', '(', '-3.5', '*', '+2', '+', '2', '^', '-2.2', '/', '4', '*', '5', '%', '6', ')', '+', '3', '-', '(-4.5)']。我们先考虑最简单的整数情况，（1+2*3）/4-2，你的代码将会如下：

def expression_spliter(expression):
    #split the expression into list, using POWERFUL REGEX MODULE to ignite your productivity 
    import re
    return re.findall('(?:[0-9\.]+|[\+\-\*\/\(\)\%\^])',expression)

真的是太炫酷了，仅用两行就解决了。我们稍作解释，(?A:B)表示匹配A模式或匹配B模式，[0-9\.]表示一个0-9或'.'的字符。反斜杠是转义字符，就是让 某些符号失去功能变为单纯的符号。后面的+表示匹配前一个字符一个或多个。因此[0-9\.]+可以表示任何小数，[\+\-\*\/\(\)\%\^] 表示匹配运算符。

但是上述代码的缺点是不能匹配符号数（包括带括号的和不带括号的），另外如果一个无符号数位于表达式最前面也需要注意。聪明的你一定能完成这项任务:-)。无论有符号数有没有括号我们都要考虑！

然后，你需要考虑如何添加括号，如果你用列表装表达式，然后用下标来索引，那么我保证你会崩溃，因为每加一次括号，下标都会改变。因此，你立马转换思路，用链表来存储吧！这是一个不错的注意我承认，但是你得实现并熟悉一个链表，这在我之前的教程里有。

下面详细讲如何添加括号。 对一个运算符 '?' 而言，它的前面和后面无异乎有四种情况：（1）数字？数字
（2）')'？数字（3）数字？'('（4）')' ? '('，如果前面后面只是数字的话，对于？前面的数字前面一位插入括号即可，后面同理。对于情况（4），我们希望得到    '(''('....')' ? '(' ....')'')'   ，红色是与？最近的括号匹配的括号，我们希望找到它们并在它们之前或之后插入粗体的括号；... 表示任意数量匹配的左括号或右括号。可以这样，举例说在？前面加括号，用一个标志l_count统计 ？前面左括号的数目，用r_count统计?前面右括号的数目。因为在最近的 ')' 里已经将r_count+1了，所以将节点不断前移p = p.prev， 其终止条件应该为r_count-l_count == 0 or p.next == None. 在？后面加括号的代码大同小异。你的代码应该如下：

def insert_brackets(r,m,ls):
    #if there is already brackets then quit
    
    if r.val == ')':
        l_count=r_count=0
        while True:
            if r.val=='(':l_count+=1
            elif r.val==')': r_count+=1
            if l_count-r_count == 0 or r.prev==None: break
            r = r.prev
    if m.val == '(':
        
        l_count=r_count=0
        while True:
            if m.val=='(':l_count+=1
            elif m.val==')': r_count+=1
            if r_count-l_count == 0 or m.next == None: break
            m = m.next

     ls.insert(r,'(','front')
     ls.insert(m,')','back')

r,m分别表示？前一个节点和后一个节点，ls表示链式堆栈。其中insert(pres_node,data,orient)是在pre_node 前或后插入node(data)的函数。 但是很快你会发现一个问题：我如何避免重复加括号，因为重复加括号没有必要而且增大计算开销降低可读性。很简单，判断左右边是否已经有匹配的括号即可，最后两行应该为：

    if r.prev!=None and  r.prev.val== '(' and m.next!=None and m.next.val==')':return
    else:
        ls.insert(r,'(','front')
        ls.insert(m,')','back')

好了，现在我们得到了一个添加括号的函数。下面要做的就是知道给什么节点添加括号。堆栈拥有LIFO的特性，非常适合来记忆元素，因为运算符符是添加括号的关键，我们新建一个栈s_oper来保存运算符符。现在，我们可以用一个字典P_dict来保存优先级，P_dict = {'^':3,'*':2,'/':2,'%':2,'+':1,'-':1,'(':0}，其中'('拥有最低的优先级。我们需要遍历表达式exp，先把exp转换为链式存储的栈，用p指向其头部。基本的遍历方法是p = p.next。有以下几种情况：

（1）如果遇到运算符或'('，则压入s_oper；

（2）如果遇到')'，就说明至少有一个'('在栈内，我们首先要把最近一组括号内的运算符按优先级和进展顺序加括号。我们先弹出一个节点oper，然后将之与栈顶的元素top进行比较，直到oper=='('时退出循环，(a) 如果oper优先级大于top，则对oper元素进行加括号，调用之前写好的insert_brackets函数；(b) 如果oper优先级小于top，我们需要继续弹栈，直到oper优先级大于top或者栈为空时停止循环；(c)如果oper优先级等于top，那么我们必须根据先后顺序来添加括号。比如 (3*5/6)，如果你添成（3*(5/6)）就是错的。为了记忆这种顺序特性，我们不得不再创建一个栈s_same_pri，如果遇到优先级相等的情况，就把从s__oper弹出的oper_temp压入堆栈；遇到oper优先级小于oper_temp时，事实上，我们得考虑这种情况，比如2^2*3/4%5，如果你按照入栈顺序加括号，得到的是2^(((2*3)/4)%5)，这显然是不对的，为此我们可以在oper优先级小于oper_temp时，直接对oper_temp加括号，然后停止循环；遇到oper优先级大于oper_temp时，直接停止循环。在s_oper中处于下面的元素在s_same_pri被翻转了过来，这样我们再把s_same_pri 弹栈，依次加括号即可。

         很不错你能看到这里，但是你不能指望马上得到漂亮的结果。因为总有些特殊情况打乱你的计划。比如括号里面有很多项，如(1+5*6/3-4^4)，你前面的代码只能得到(1+((5*6)/3)-(4^4))，你希望的是(1+(((5*6)/3)-(4^4)))或者((1+((5*6)/3))-(4^4))。如果你一开始能想到最极端的情况，这对你的调试总是有很大的帮助。连接项与项的要么是“+”要么是“-”，因为它们的优先级为1，仅高于“(”。这时候，你又想到了堆栈，“不是吧，又要用堆栈？”我猜你肯定会这样想。但是事实就是如此，你必须反复使用基础的数据结构，它们是如此的重要！可以用一个新的栈s_item来存储项，但其实不用，我们只用“记录”连接项的“+”或“-”即可。在括号内所有的子项都加完括号后，我们就可以把s_item依次弹出在项之间加括号，直到栈为空停止。

好了，对exp遍历完之后，我们已经处理了含括号的部分，但是s_oper内还有一些节点，它们是在括号外面（相对而言）。Smart as you are, 你知道它们可以像括号内的情况一样处理。我们先弹出一个节点oper，然后将之与栈顶的元素top进行比较，直到栈为空时退出循环，(a) 如果oper优先级大于top，则对oper元素进行加括号，调用之前写好的insert_brackets函数；(b) 如果oper优先级小于top，我们需要继续弹栈，直到oper优先级大于top或者栈为空时停止循环；(c) 如果oper优先级等于top，那么我们必须根据先后顺序来添加括号。比如 (3*5/6)，如果你添成（3*(5/6)）就是错的。为了记忆这种顺序特性，我们不得不再创建一个栈s_same_pri，如果遇到优先级相等的情况，就把从s__oper弹出的oper_temp压入堆栈；遇到oper优先级小于oper_temp时，事实上，我们得考虑这种情况，比如2^2*3/4%5，如果你按照入栈顺序加括号，得到的是2^(((2*3)/4)%5)，这显然是不对的，为此我们可以在oper优先级小于oper_temp时，直接对oper_temp加括号，然后停止循环；遇到oper优先级大于oper_temp时，直接停止循环。在s_oper中处于下面的元素在s_same_pri被翻转了过来，这样我们再把s_same_pri 弹栈，依次加括号即可。项与项之间的处理和上一段相同。

最后将链表转换为列表输出即可。

---

下面是笔者得到的部分结果,考虑了有符号数情况。

是否感觉自己的脑容量增加了呢，希望本文对你有帮助！

PS 笔者3.29日完成V1.0代码，到今天4.15 V11.0 经过无数测试后仍发现bug，无论如何，笔者在代码完善之后会上传。不断发现bug，修改bug这大概就是程序猿的宿命吧。

---

如果你实现了模方^，那么问题来了。它的优先级最高一定为3. 我们考虑一种极特殊情况，5/0.5^5%2*3，也就是说在^后仍然有两个及以上的*或/，那么上述代码将失效，在括号里面和外面都是一样的。我们必须首先对'^'符号进行加括号，然后依次按照/%*顺序加括号。现在请聪明的你想想应该如何解决这个问题。。。

。。。

很棒！你已经得到答案了。问题在于判断某个运算符X与下个运算符优先级相同情况中，我们遇到了s_oper弹出运算符优先级打于X时最后加上了break。这样它不会判断前面的运算符。我们把break去掉。但这样s_oper有可能弹空，所以处理括号内容时结束条件由oper.val=='('改为not oper or oper.val=='('更为合适。 

笔者在测试时发现(5/6^5+1)/0.5^5+2这样的简单情况也有问题，原因是在括号外，如果只有一个优先级为2的运算符则不会对此运算符加括号，我们在判断s_oper为空break之前，增加一个条件，若弹出的运算符不为None，对其加括号。

在 python中，不为None的变量都可以视为True。