DP斜率优化 【HDU3507】 【洛谷P2900】

例题：HDU3507

这是一个优秀的斜率优化原理说明。。。

我的代码如下： 

#include
#define maxn 1000000
using namespace std;

int n,m,dp[maxn],q[maxn],s[maxn],a[maxn];

int sqr(int x) {return x*x;}

int get_x(int x,int y) {
	return s[y]-s[x];
}

int get_y(int x,int y) {
	return dp[y]-dp[x]+sqr(s[y])-sqr(s[x]);
}

int main() {
	int i,nowk,f,l;
	while (scanf("%d%d",&n,&m)!=EOF) {
		for (i=1;i<=n;i++) {
			scanf("%d",&a[i]);
			s[i]=s[i-1]+a[i];
		}
		f=l=0;
		for (i=1;i<=n;i++) {
			nowk=s[i]<<1;
			while (f=get_y(q[l],i)*get_x(q[l-1],q[l])) l--; 
			//维护单调队列的单调性，即使队列中存的东西构成一个下凸包。
			q[++l]=i;
		}
		printf("%d\n",dp[n]);
	}
	return 0;
}

 斜率优化是一种对于满足某些要求的$DP$方程进行形式上的优化，运用了单调队列的思想，能够大大降低时间复杂度，在本题中起到的作用就是快速地（O(1)）求出dp[i]应该从哪个dp[j](j∈1~i-1)转移而来。

太难了，所以我只会这一题QAQ

upd:现在不只了哈哈

再来一道题，看出来DP方法了就比HDU3507还简单。

洛谷P2900 [USACO08MAR]土地征用

双倍经验

首先将所给出的矩形按长度（宽度也可）为第一关键字排一次序，将散乱的矩形整理一下，保证后面的矩形一定会比前面的矩形长度更长。

（这样有什么意义？保证长度的单调性，即a[i].l随i的增长而增长，确保斜率优化的先决条件。）

（虽然在现在我们不知道这道题目要用到斜率优化，排序仅仅是为了方便DP）

然后会发现排完序后会存在一些矩形，它比它之前的矩形长度更大，宽度更大，所以把它和它之前的矩形一起卖掉相当于只买它。所以可以发现，这个前面的小矩形没有意义，可以直接删掉。

剩下的矩形如下图：

这时的矩形长度逐渐递增，且宽度逐渐递减。

然后怎样合并矩形可以得到最小值呢？

考虑到DP

方程如下：

dp[i]——合并到第i个矩形（包含i）时的总面积最小值

显然有（在j+1~i这些矩形中，a[j+1].w显然是最大宽度，a[i].l显然是最大长度，一次转移表示合并一次）

那么有一个重要的问题：凭什么我一定要按照这些矩形的顺序来合并？

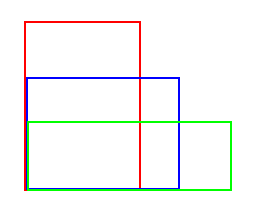
请看下图：

显然如果我合并了红色和绿色，那么蓝色就会包含在红绿合并成的大矩形里！

 所以。。。你会发现TLE了（O(n²)）

O(n)？

观察DP方程：

当存在k（毕竟是求min值嘛）

转化一下式子形成斜率的形式：

所以仿照之前的HDU3507，就可以写出很好的DP代码了QwQ！

#include
#include
#include
#include
#define maxn 80010
#define int long long
using namespace std;

struct node {
    int l,w;
}a[maxn];

int n,q[maxn],dp[maxn];

bool cmp(node a,node b) {return (a.l=a[now].w) now--;
        a[++now].l=a[i].l;
        a[now].w=a[i].w;
    }
    n=now;
    f=l=0;
    for (i=1;i<=n;i++) {
        while (f=get_k(q[l],i)) l--;
        q[++l]=i;
    }
    printf("%lld\n",dp[n]);
    return 0;
}

update2 :

斜率优化推式子的另一种方式：

将与转移量线性相关的东西丢到一边当做,

将有关转移量的乘积项丢到另一边当做,常数项（和有关状态量的常数项）当做.