GIS判断点线面空间关系的思路
1、直线的斜率
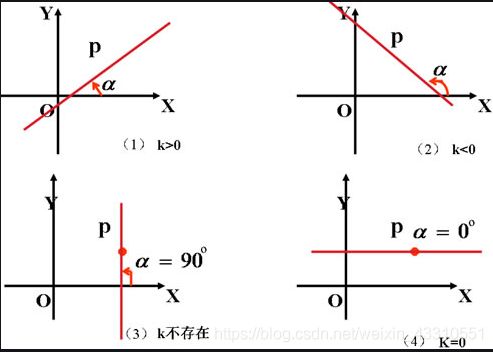
直线斜率(k)是直线与X轴右侧(正半轴方向)所成角的正切值。
k=Math.tan(α) => -无穷 < k < 无穷
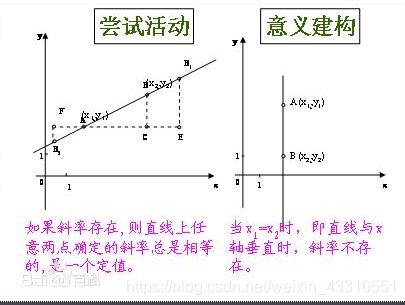
假设有直线段L,直线上已知2点分别为A(x1,y1)、B(x2,y2),那么直线段L的斜率:
k=tanα=(y2-y1)/(x2-x1)=(y1-y2)/(x1-x2)
如果有一点P(x,y),判断P是否在直线L上,
①如果P在直接L上,那么P点和A点以及P和B点构成的线段斜率都和直线L的斜率相等
(y-y1)/ (x-x1)= k =y2-y1)/(x2-x1)=(y1-y2)/(x1-x2) =>
(y-y1) / (x-x1) - (y2-y1) / (x2-x1)=0
②、如果点P不在直线上,如何判断点P在直线的哪一边?
(y-y1) / (x-x1) -(y2-y1) / (x2-x1) > 0 ,点P在线段的左边
(y-y1) / (x-x1) -(y2-y1) / (x2-x1) < 0, 点P在线段的右边
以上换成代码:
1、如果直线的斜率不存在,A和B两点的X坐标相等:
// 直线斜率k=tanα=(y2-y1)/(x2-x1)=(y1-y2)/(x1-x2)
/**
* 判断点和直线的关系
* 已知直线L上2点 A(x1,y1)、B(x2,y2),求点P(x,y)和直线的关系:①、点在直线上; ②、点在直线左边; ③、点在直线右边
* @param {*} A 已知坐标的直线上一点A
* @param {*} B 已知坐标的直线上一点B
* @param {*} P P是需要判断和直线关系的点,坐标已知
*/
function pointWithLineRelation(P,A,B){
let x1=A.x,y1=A.y,
x2=B.x,y2=B.y,
x=P.x,y=P.y ;
if(x1!==x2){
//直线斜率存在
if(y1===y1){
//斜率为0
if(y===y1){
console.log('点在直线上');
return 'onLine';
}else if(y < y1){
console.log('点在直线下面');
return 'bottom';
}else{
console.log('点在直线上面');
return 'top';
}
}
let k=(y2-y1) / (x2-x1);//直线斜率 k=(y2-y1) /(x2-x1)=(y1-y2) /(x1-x2)
//求P和直线上任一点的斜率 kx
let kx=(y-y1) / (x-x1);
if(kx - k===0){
console.log('点在直线上');
return 'onLine';
}else if(kx - k >0){
console.log('点在直线左侧');
return 'left';
}else if(kx - k <0){
console.log('点在直线右侧');
return 'right';
}
}else{
//直线斜率不存在 x1===x2
if(x===x1){
console.log('点在直线上');
return 'onLine';
}else if(x < x1){
console.log('点在直线左侧');
return 'left';
}else{
console.log('点在直线右侧');
return 'right';
}
}
}
/**
* 判断2条线段是否相交,假设有线段L1,顶点分别为A1、B1;线段L2,顶点分别为A2、B2。
* 数学定理:如果线段L1和L2相交,那么线段L1的2个顶点应该分别位于线段L2的两侧,并且线段L2的2个顶点也应该分别位于线段L1的2侧,
* 否则,2条线段就是不相交的。
*
* @param {*} coordArry1 线段L1的顶点坐标 形如[{x:2,y:0},{x:5,y:5}]
* @param {*} coordArry2 线段L2的顶点坐标 形如[{x:4,y:0},{x:7,y:8}]
*/
function linWithLineRelation(coordArry1,coordArry2){
let L1p1=coordArry1[0],L1p2=coordArry1[1]; //线段L1上的2个顶点L1P1、L1P2
let L2p1=coordArry2[0],L2p2=coordArry2[1]; //线段L1上的2个顶点L1P1、L1P2
let k1=(L1p2.y - L1p1.y) / (L1p2.x - L1p1.x);
let k2=(L2p2.y - L2p1.y) / (L2p2.x - L2p1.x);
if(k1===k2){
console.log('2条线段斜率相等,不相交');
return false;
}
//求线段L1的第1个顶点和线段L2的关系
let L1p1WithL2=pointWithLineRelation(L1p1,L2p1,L2p2);
//求线段L1的第2个顶点和线段L2的关系
let L1p2WithL2=pointWithLineRelation(L1p2,L2p1,L2p2);
//求线段L2的第1个顶点和线段L1的关系
let L2p1WithL1=pointWithLineRelation(L2p1,L1p1,L1p2);
//求线段L2的第2个顶点和线段L1的关系
let L2p2WithL1=pointWithLineRelation(L2p2,L1p1,L1p2);
if(L1p1WithL2 !==L1p2WithL2 && L2p1WithL1!==L2p2WithL1){
console.log('2条线段不相交');
return false;
}else{
console.log('2条线段相交');
return true;
}
}
/**
* 求空间面polygon1 和面polygon2 是否相交,可以把面和面的相交分解为求线段和线段是否相交,分别把 polygon1按每2个相邻顶点拆分成线,polygon2也同样按每2个相邻顶点拆分成线;然后用 polygon1拆分后的线段逐一 和 polygon2拆分后的每一条线段做相交关系判断,如果polygon1每一条线段都和polygon2的其中任何一条线段没有交点,那么2个面就是不相交的,否则,2个面就是相交的。
*
*/