C++力扣刷题记录——动态规划(持续更新)
动态规划思路
-
确定DP状态
最优子结构:当前DP状态可以由小的DP状态求
无后效:当前求得与小的求得的过程无关 -
确定转移方程
根据分类讨论确定 -
写程序
要注意边界条件以及初始条件的撰写
1乘积最大子数组
给一个数组,返回乘积最大的值
思路:
自然而然想到DP状态为:右端为i的最大乘积
但是右端为i最大的与右端为i-1 或者i-2最大的值无关。不满足最优子结构啊。
(分析不满足的原因主要是因为 当前值为负数或者为正数的时候不一样)
DP状态:
if(A[i]>0)
f[i]=max(A[i],max(f[i-1])*A[i]);
else
f[i]=max(A[i],min(f[i-1])*A[i]);
这样就可以了
DP转移方程:
看DP状态,需要求的东西为
max(f[i-1])
min(f[i-1])
也要分类讨论了
if(A[i]>0){
maxf[i]=max(A[i],maxf[i-1]*A[i]);
minf[i]=min(A[i],minf[i-1]*A[i]);
}
else{
maxf[i]=max(A[i],minf[i-1]*A[i]);
minf[i]=min(A[i],maxf[i-1]*A[i]);
}
然后就可以写程序了 不过需要注意的是边缘条件
class Solution{
public:
vector<int>maxf,minf;
int maxProduct(vector<int>& nums){
int n=nums.size();
int ans = nums[0];//边界条件
maxf.resize(n);
minf.resize(n);
for(int i=1;i<n;i++){//0的时候放哪里都不行
if(nums[i]>0)
{
maxf[i]=max(nums[i],maxf[i-1])*nums[i];
minf[i]=min(nums[i],maxf[i-1])*nums[i];
}
else
{
maxf[i]=max(nums[i],minf[i-1]*num[i]);
minf[i]=min(nums[i],maxf[i-1]*num[i]);
}
ans=ans>maxf[i]?ans:maxf[i];
}
return ans;
}
}
2:1139. 最大的以 1 为边界的正方形
给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。

#include 放出调试代码。自己写的时候没有注意c和kk 判断内循环写了kk,气死了
看到一个代码比我简单的
class Solution {
public:
int largest1BorderedSquare(vector<vector<int>>& grid) {
int length = grid.size();//矩阵的长
if (length == 0) return 0;
int width = grid[0].size();//矩阵的宽
//用dp[i][j][0]来表示第i行第j列的 左边 连续的1的个数
//用dp[i][j][1]来表示第i行第j列的 上面 连续的1的个数
vector<vector<vector<int>>> dp(length + 1, vector<vector<int>>(width + 1, vector<int>(2, 0)));
int maxLen = 0;
for (int i = 1; i <= length; i++) {
for (int j = 1; j <= width; j++) {
if (grid[i - 1][j - 1] == 1) {
dp[i][j][0] += dp[i][j - 1][0] + 1;
dp[i][j][1] += dp[i - 1][j][1] + 1;
//尝试以第i行第j列(当前点)为右下角构成正方形
int len = min(dp[i][j][0], dp[i][j][1]);//最大可能长度
while (len > 0) {
//判断这个可能的正方形右上角左侧是否有连续len个1 && 左下角的上方是否有连续len个1
if (dp[i - len + 1][j][0] >= len && dp[i][j - len + 1][1] >= len)
break;
len--;
}
maxLen = max(maxLen, len);
}
}
}
return maxLen * maxLen;
}
};
作者:koishi-7
链接:https://leetcode-cn.com/problems/largest-1-bordered-square/solution/c-dong-tai-gui-hua-by-koishi-7/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
区别在于他把边缘条件变得更加简单了。很厉害~
3 面试题 08.11. 硬币
硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007)
思路是找DP状态为f(i,v)=f(i-1,v-c(i))+f(i-1,v-2c(i))+f(i-1,v-3c(i))…+f(i-1,v-kc(i));
f(i,v-ci)=f(i-1,v-2c(i))+f(i-1,v-3c(i))…+f(i-1,v-kc(i))
可得到f(i,v)=f(i-1,v-c(i))+f(i,v-ci);
然后就建表,注意边缘情况
#include 4 不同的二叉搜索树
思路:
f(n)为n个节点可以组成几棵树
0个节点f(0)=1-一棵空树
1个节点f(1)=1
2个节点f(2)=f(1)f(0)+f(0)f(1)-选定一个头节点后剩下的1个节点 和0个节点怎么分配
3个节点f(3)=f(2)(0)+f(1)f(1)+f(0)f(2)
所以
f(n)=f(n-1)f(0)+f(n-2)f(1)+…
class Solution {
public:
int numTrees(int n) {
vector<int> f(n+1, 0);
f[0]=1;
for (int j=1;j<=n;j++)
{
for (int i = 0; i < j; i++)
{
f[j] += f[i] * f[j -1- i];
}
}
return f[n];
}
};
5 740 删除获得点数
给定一个整数数组 nums ,你可以对它进行一些操作。
每次操作中,选择任意一个 nums[i] ,删除它并获得 nums[i] 的点数。之后,你必须删除每个等于 nums[i] - 1 或 nums[i] + 1 的元素。
开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。
刚写了一堆没有保存。cao
dp状态时1-i个数的时候的最大
dp[i]=max(dp[i-1],dp[i-2]+i对应的整个的和)
#include 6 0-1背包问题
有n个物品,它们有各自的重量w和价值v,现有给定容量C的背包,如何让背包里装入的物品具有最大的价值总和?
0-1背包问题指的是每个物品只能使用一次

思路:
有N件物品和一个容量为C的背包。(每种物品均只有一件)
第i件物品的重量是w[i],价值是v[i]。求解将哪些物品装入背包可使价值总和最大。
这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。用子问题定义状态:
DP状态:f[i][c]表示前i件物品放入一个容量为c的背包可以获得的最大价值。
关键点来了:对于第i个物体,其实就是两种可能,一种是选,一种是不选
如果选了,那么问题就变成了 f[i-1][c-w[i]],如果没选那么就变成f[i-1][c]
f[i][c]=max(f[i-1][c-w[i]]+v[i],f[i-1][c]);比较谁的价值大就是谁
初值就是需要考虑 i=0,f=0;c=0,f=0
7 剑指 Offer 42. 连续子数组的最大和
输入一个整型数组,数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
思路:
DP状态为右端为n的时候最大连续子数组和的最大值f[n]
f[n]就两种情况,一种是f[n-1]>0,那么就是f[n-1]+nums[i]
如果f[n-1]<0.那么就是nums[i]
转移方程就便成了
max(f[n-1]+nums[i],nums[i]);
实现代码为
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int NumsSize = nums.size();
vector<int> dp(NumsSize, 0);
dp[0] = nums[0];
int MaxV = dp[0];
for (int i=1;i<NumsSize;i++){
dp[i] = max(dp[i - 1] + nums[i], nums[i]);
MaxV = max(MaxV, dp[i]);
}
return MaxV;
}
};
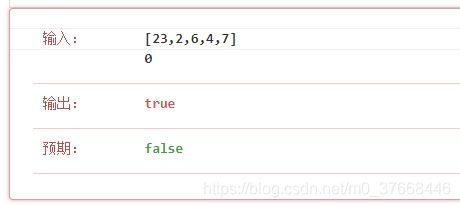
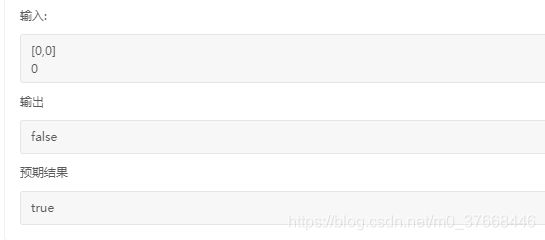
8 523 连续子数组和
给定一个包含 非负数 的数组和一个目标 整数 k,编写一个函数来判断该数组是否含有连续的子数组,其大小至少为 2,且总和为 k 的倍数,即总和为 n*k,其中 n 也是一个整数。

class Solution {
public:
bool checkSubarraySum(vector<int>& nums, int k) {
if (nums.size() < 2)
return false;
//左边为第1,右边为第n的数组
vector<int> f(nums.size() + 1, 0);
f[1] =nums[0];
for (int i = 2; i < nums.size() + 1; i++) {
f[i] = nums[i - 1] + f[i - 1];
if(f[i]==0)
return true;
int sum = f[i];
if(k!=0){
if (sum%k==0)
return true;
}
for (int j = 0; j < i - 2; j++) {
sum -= nums[j];
if (sum == 0)
return true;
if(sum==0&&k==0)
return true;
if (k == 0)
continue;
else if (sum%k == 0) {
return true;
}
}
}
return false;
}
};
9 198 打家劫舍Ⅰ
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
思路
很明显的是动态规划的问题。
dp[i]=max(dp[i-1],dp[i-2]+nums[n])
dp[i]是数组到i的最大数额:
仔细分析可以法线其可以分成
如果最大包含了nums[i-1]那么新加的nums[i]是不可以加进去的,最大的为dp[i-1]
如果没有包含nums[i-1]那么说明 dp[i-1]=dp[i-2]的 最大的为dp[i-2]+nums[i]
比一下 大的就是了 注意原始条件。dp[1] dp[2]
class Solution {
public:
int rob(vector<int>& nums) {
if (nums.empty())return 0;
int size = nums.size();
vector<int> dp(size + 1, 0);//size个值为0的int
dp[1] = nums[0];
if(size>=2) dp[2] = max(nums[0], nums[1]);
for (int i = 3; i <= size; i++) {
dp[i] = max(dp[i - 2] + nums[i - 1], dp[i - 1]);
}
return dp[size];
}
};
需要注意的地方是:
if(size>=2) dp[2] = max(nums[0], nums[1]);开始没有考虑nums[1]可能溢出的问题。
10 213 打家劫舍Ⅱ
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
思路:
分三种情况 三个里面最大的就是我们要的 其实我们可以不考虑情况1
因为这两种情况对于房子的选择余地比情况一大呀,房子里的钱数都是非负数,所以选择余地大,最优决策结果肯定不会小。
这个题目是第一种的一个延伸max(情况1,情况2)
class Solution {
public:
//有三种情况,抢1不能抢尾巴 抢尾巴不能抢1,都不抢
int rob(vector<int>& nums) {
if (nums.empty())return 0;
int size = nums.size();
vector<int> dp1(size + 1, 0);//不抢1
vector<int> dp2(size + 1, 0);//不抢尾巴
dp1[1] = 0;
if (size > 1)dp1[2] = nums[1];
if (size > 2)dp1[3] = max(nums[1], nums[2]);
for (int i = 4; i <= size; i++) {
dp1[i] = max(dp1[i - 2] + nums[i - 1], dp1[i - 1]);
}
dp2[1] = 0;
if (size > 1)dp2[2] = nums[0];
if (size > 2)dp2[3] = max(nums[1], nums[0]);
for (int i = 4; i <= size; i++) {
dp2[i] = max(dp2[i - 2] + nums[i - 2], dp2[i - 1]);
}
dp1[1] = nums[0];
return max(dp1[size], dp2[size]);
}
};
11 337. 打家劫舍 III
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
思路
我们可以用 f(o)f(o) 表示选择 oo 节点的情况下,oo 节点的子树上被选择的节点的最大权值和;g(o)g(o) 表示不选择 oo 节点的情况下,oo 节点的子树上被选择的节点的最大权值和;ll 和 rr 代表 oo 的左右孩子。
当 oo 被选中时,oo 的左右孩子都不能被选中,故 oo 被选中情况下子树上被选中点的最大权值和为 ll 和 rr 不被选中的最大权值和相加
即 f(o) = g(l) + g®f(o)=g(l)+g®。
当 oo 不被选中时,oo 的左右孩子可以被选中,也可以不被选中。对于 oo 的某个具体的孩子 xx,它对 oo 的贡献是 xx 被选中和不被选情况下权值和的较大值。故 g(o) = \max { f(l) , g(l)}+\max{ f® , g® }g(o)=max{f(l),g(l)}+max{f®,g®}。
class Solution {
public:
unordered_map <TreeNode*, int> f, g;
void dfs(TreeNode* o) {
if (!o) {
return;
}
dfs(o->left);
dfs(o->right);
f[o] = o->val + g[o->left] + g[o->right];
g[o] = max(f[o->left], g[o->left]) + max(f[o->right], g[o->right]);
}
int rob(TreeNode* o) {
dfs(o);
return max(f[o], g[o]);
}
};