IMU-Allan方差分析
使用Allan方差来确定MEMS陀螺仪的噪声参数,陀螺仪测量模型为:
![]()
使用长时间静止的陀螺仪数据对陀螺仪噪声参数进行分析,上式中,三个噪声参数N(角度随机游走),K(速率随机游走)和B(偏差不稳定性)。
背景
Allan方差最初由David W. Allan开发,用于测量精密仪器的频率稳定性。 它还可用于识别固定陀螺仪测量中存在的各种噪声源。对于一份陀螺仪样本数据,其采样时间为 τ 0 \tau_{0} τ0,数据集合的长度分别为 τ 0 , 2 τ 0 , … , m τ 0 , ( m < ( L − 1 ) / 2 ) \tau_{0}, 2 \tau_{0}, \ldots, m \tau_{0},(m<(L-1) / 2) τ0,2τ0,…,mτ0,(m<(L−1)/2),获得在每段数据上的平均值,Allan方差定义为数据平均值的样本方差,Allan方差在数据量较大时精度较高。
Allan方差的计算
采样时间为 τ 0 \tau_{0} τ0, Ω \Omega Ω每一段的数据样本集合。
% Load logged data from one axis of a three-axis gyroscope. This recording
% was done over a six hour period with a 100 Hz sampling rate.
load('LoggedSingleAxisGyroscope', 'omega', 'Fs')
t0 = 1/Fs;
对每一段样本,计算输出角 θ \theta θ:
![]()
对于离散样本,使用乘法对其进行积分:
theta = cumsum(omega, 1)*t0;
然后计算Allan方差:
![]()
其中 τ \tau τ=m τ 0 \tau_{0} τ0,<>为整体平均值
整体平均值可以扩展为:
![]()
maxNumM = 100;
L = size(theta, 1);
maxM = 2.^floor(log2(L/2));
m = logspace(log10(1), log10(maxM), maxNumM).';
m = ceil(m); % m must be an integer.
m = unique(m); % Remove duplicates.
tau = m*t0;
avar = zeros(numel(m), 1);
for i = 1:numel(m)
mi = m(i);
avar(i,:) = sum( ...
(theta(1+2*mi:L) - 2*theta(1+mi:L-mi) + theta(1:L-2*mi)).^2, 1);
end
avar = avar ./ (2*tau.^2 .* (L - 2*m));
最后,Allan方差 σ ( t ) = σ 2 ( t ) \sigma(t)=\sqrt{\sigma^{2}(t)} σ(t)=σ2(t)用于确定陀螺仪噪声参数。
adev = sqrt(avar);
figure
loglog(tau, adev)
title('Allan Deviation')
xlabel('\tau');
ylabel('\sigma(\tau)')
grid on
axis equal
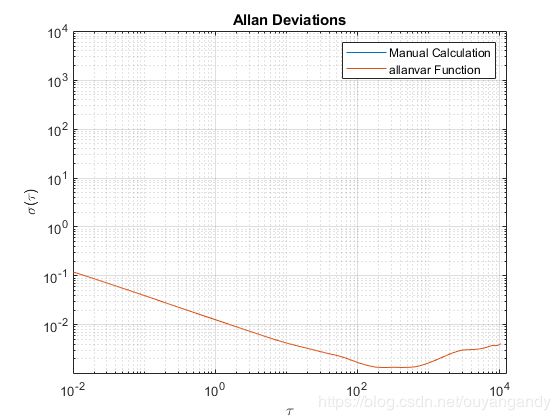
结果如下(Allan方差曲线):

在MATLAB中可以使用Allan方差的函数:
[avarFromFunc, tauFromFunc] = allanvar(omega, m, Fs);
adevFromFunc = sqrt(avarFromFunc);
figure
loglog(tau, adev, tauFromFunc, adevFromFunc);
title('Allan Deviations')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('Manual Calculation', 'allanvar Function')
grid on
axis equal
噪声参数分析
要获得陀螺仪的噪声参数,使用Allan方差与原始数据集中噪声参数的双侧功率谱密度(PSD)之间的以下关系:
![]()
根据上式,当通过具有传递函数 sin 4 ( x ) / ( x ) 2 \sin ^{4}(x) /(x)^{2} sin4(x)/(x)2时,Allan方差与陀螺仪总噪声功率成正比关系,使用传递函数解释,带通取决于 τ \tau τ,这意味着可以通过改变滤波器带通或改变 τ \tau τ来获取不同的噪声参数。
Angle Random Walk-角度随机游走
角度随机游走被定义为陀螺仪输出的白噪声频谱,其功率谱密度可以表示为:
![]()
其中N代表了角度随机游走系数,代入原始PSD方程并执行积分:
![]()
上面的等式是在log-log图上绘制的斜率为-1/2的线。 N的值可以直接从该行读取。
% Find the index where the slope of the log-scaled Allan deviation is equal
% to the slope specified.
slope = -0.5;
logtau = log10(tau);
logadev = log10(adev);
dlogadev = diff(logadev) ./ diff(logtau);
[~, i] = min(abs(dlogadev - slope));
% Find the y-intercept of the line.
b = logadev(i) - slope*logtau(i);
% Determine the angle random walk coefficient from the line.
logN = slope*log(1) + b;
N = 10^logN
% Plot the results.
tauN = 1;
lineN = N ./ sqrt(tau);
figure
loglog(tau, adev, tau, lineN, '--', tauN, N, 'o')
title('Allan Deviation with Angle Random Walk')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('\sigma', '\sigma_N')
text(tauN, N, 'N')
grid on
axis equal
N =
0.0126
Rate Random Walk
陀螺仪输出的红噪声(布朗噪声)频谱被定义为Rate Random Walk ,PSD(功率谱密度)如下:
![]()
其中K为Rate Random Walk系数,代入原始PSD方程并执行积分:
![]()
上面的等式是在log-log图上绘制的斜率为-1/2的线。 N的值可以直接从该行读取。
% Find the index where the slope of the log-scaled Allan deviation is equal
% to the slope specified.
slope = 0.5;
logtau = log10(tau);
logadev = log10(adev);
dlogadev = diff(logadev) ./ diff(logtau);
[~, i] = min(abs(dlogadev - slope));
% Find the y-intercept of the line.
b = logadev(i) - slope*logtau(i);
% Determine the rate random walk coefficient from the line.
logK = slope*log10(3) + b;
K = 10^logK
% Plot the results.
tauK = 3;
lineK = K .* sqrt(tau/3);
figure
loglog(tau, adev, tau, lineK, '--', tauK, K, 'o')
title('Allan Deviation with Rate Random Walk')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('\sigma', '\sigma_K')
text(tauK, K, 'K')
grid on
axis equal
K =
9.0679e-05
Bias Instability 零偏不稳定性
零偏不稳定性被定义为陀螺仪输出的粉红噪声频谱pink noise(闪烁噪声-flicker noise),功率谱密度表示如下:
![]()
其中B为零偏不稳定性系数, f 0 f_{0} f0为截止频率。
代入原始PSD方程并执行积分:
![]()
其中:
![]()
C i Ci Ci =余弦积分函数.其中, τ \tau τ远大于截止频率的倒数时,PSD方程为:
![]()
当绘制在对数图上时,上面的等式是斜率为0的直线。 B的值可以直接从该行读取,缩放比例为:
![]()
% Find the index where the slope of the log-scaled Allan deviation is equal
% to the slope specified.
slope = 0;
logtau = log10(tau);
logadev = log10(adev);
dlogadev = diff(logadev) ./ diff(logtau);
[~, i] = min(abs(dlogadev - slope));
% Find the y-intercept of the line.
b = logadev(i) - slope*logtau(i);
% Determine the bias instability coefficient from the line.
scfB = sqrt(2*log(2)/pi);
logB = b - log10(scfB);
B = 10^logB
% Plot the results.
tauB = tau(i);
lineB = B * scfB * ones(size(tau));
figure
loglog(tau, adev, tau, lineB, '--', tauB, scfB*B, 'o')
title('Allan Deviation with Bias Instability')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('\sigma', '\sigma_B')
text(tauB, scfB*B, '0.664B')
grid on
axis equal
B =
0.0020

现在已经计算了所有噪声参数,将Allan偏差绘制为量化参数的所有线。

陀螺仪仿真
使用imu传感器基于上面确定的噪声参数模拟陀螺仪测量。
% Simulating the gyroscope measurements takes some time. To avoid this, the
% measurements were generated and saved to a MAT-file. By default, this
% example uses the MAT-file. To generate the measurements instead, change
% this logical variable to true.
generateSimulatedData = false;
if generateSimulatedData
% Set the gyroscope parameters to the noise parameters determined
% above.
gyro = gyroparams('NoiseDensity', N, 'RandomWalk', K, ...
'BiasInstability', B);
omegaSim = helperAllanVarianceExample(L, Fs, gyro);
else
load('SimulatedSingleAxisGyroscope', 'omegaSim')
end
计算模拟的Allan偏差并将其与记录的数据进行比较:
[avarSim, tauSim] = allanvar(omegaSim, 'octave', Fs);
adevSim = sqrt(avarSim);
adevSim = mean(adevSim, 2); % Use the mean of the simulations.
figure
loglog(tau, adev, tauSim, adevSim, '--')
title('Allan Deviation of HW and Simulation')
xlabel('\tau');
ylabel('\sigma(\tau)')
legend('HW', 'SIM')
grid on
axis equal
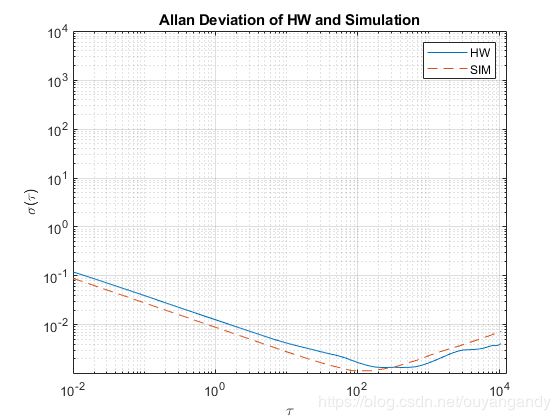
该图显示,从imuSensor创建的陀螺仪模型生成的测量值与记录的数据具有相似的Allan偏差。 模型测量包含的噪声略小,因为温度相关参数不是使用gyroparams设置的。
说明
本文按照MATHWORKS文档进行主观翻译,如有不当之处欢迎指出。
本文代码使用的MATLAB的版本为matlab2019a,基于Sensor Fusion and Tracking Toolbox。