IIR数字滤波器的设计(详细,快速入门)
IIR数字滤波器的设计
Mrakdown常见数学符号
Markdown基础语法
冲激响应不变法
-
冲激响应不变法:就是用其单位冲激响应序列模仿模拟滤波器的单位冲激响应的抽样值
-
设计的具体步骤及方法
首先要设计一个响应的模拟滤波器。
模拟滤波器的单位冲激响应非周期 ⇒ \Rightarrow ⇒ 频率离散(- ∞ \infty ∞-+ ∞ \infty ∞ ),频谱范围可能大于折叠频率,即奈奎斯特频率 ⇒ \Rightarrow ⇒ 取样,频率周期延拓 ⇒ \Rightarrow ⇒ 频谱可能产生混叠。
数字域中极点在单位圆内 ⇔ \Leftrightarrow ⇔模拟域中极点在左半平面。
可以通过提高抽样频率来减少混叠,但设计指标若以数字域频率给定时,不能通过提高抽样频率改善混叠现象。因为 Ω = ω T \Omega=\frac{\omega}{T} Ω=Tω , ω \omega ω是数字域频率, Ω \Omega Ω是模拟域频率,增大抽样频率 ⇒ \Rightarrow ⇒减小采样周期 ⇒ \Rightarrow ⇒增大截止频率。 模拟域 :Ha(s) = ∑ k = 1 N A k s − s k \sum_{k=1}^N \frac{A_k}{s-s_k} ∑k=1Ns−skAk 数字域:H(z) = ∑ k = 1 N A k 1 − e s k T z − 1 \sum_{k=1}^N \frac{A_k}{1-e^{s_kT}z^{-1}} ∑k=1N1−eskTz−1Ak
s平面:s=sk z平面:z= e s k T e^{s_kT} eskT 两者系数相同
当采样周期很小时,数字滤波器增益很大,容易溢出,可以修正,令h(n)=T h a ( n T ) h_a(nT) ha(nT),因为H(ejw)= 1 T H a ( j ω T ) \frac{1}{T}H_a(j\frac{\omega}{T}) T1Ha(jTω)
该方法对应的MATLAB程序:[BZ, AZ] = impinvar(B,A,Fs),其中BZ,AZ为数字滤波器单位冲击响应的分子和分母系数;B,A为模拟滤波器的分子和分母的系数,Fs为抽样频率。 -
优点
- 时域逼近良好
- 保持线性关系: ω \omega ω= Ω \Omega ΩT
-
缺点
- 频率响应混叠,只适用低通、带通滤波器。
阶跃响应不变法
- 变换原理:数字滤波器的阶跃响应模仿模拟滤波器的阶跃响应,即g(n)=ga(t)|t=nt=ga(nT).
- g(n)=u(n)*h(n) → \rightarrow → G(z)= z z − 1 H ( z ) \frac{z}{z-1}H(z) z−1zH(z) ,ga(t)=u(t)*ha(t) → \rightarrow →Ga(s)= 1 s H a ( s ) \frac{1}{s}H_a(s) s1Ha(s)
变换步骤:
H a ( s ) → G a ( s ) → g a ( t ) → g ( n ) → G ( z ) → H ( z ) H_a(s)\rightarrow G_a(s)\rightarrow g_a(t)\rightarrow g(n)\rightarrow G(z)\rightarrow H(z) Ha(s)→Ga(s)→ga(t)→g(n)→G(z)→H(z) - 优缺点同冲激响应不变法
双线性不变法
- 为什么需要双线性变换法?–避免频谱混叠
在推导过程中有一个中间域,最终的关系式为z= 1 + s 1 − s \frac{1+s}{1-s} 1−s1+s ,为了使模拟滤波器与数字滤波器的某一频率有对应关系,引入一个常数c,则有s=c 1 − 1 z 1 + 1 z \frac{1-\frac{1}{z}}{1+\frac{1}{z}} 1+z11−z1 ,即z= c + s c − s \frac{c+s}{c-s} c−sc+s。若低频处有确切的对应关系应为c= 2 T \frac{2}{T} T2 。
s平面虚轴与z平面单位圆的对应关系 Ω \Omega Ω =ctan w 2 \frac{w}{2} 2w Ω \Omega Ω 为s域,w为数字域
-
优点:无频率混叠,避免了多值映射。
-
缺点:除零频率附近,严重非线性关系,在临界频率点(通带截止频率和阻带截止频率–这个是技术指标)产生畸变。
-
解决临界频率点的畸变–预畸变
Ω \Omega Ω =c tan w 2 \tan\frac{w}{2} tan2w ,在临界频率点根据w去设计 Ω \Omega Ω ,再去设计模拟滤波器,再用双线性变换法设计数字滤波器 -
该方法对应的MATLAB方法:[BZ, AZ] = bilinear(B,A,Fs)
常用模拟滤波器设计
- 由幅度平方函数确定模拟滤波器的系统函数
∣ H a ( j Ω ) ∣ 2 = H a ( j Ω ) H a ∗ ( j Ω ) = H a ( j Ω ) H a ( − j Ω ) = H a ( s ) H a ( − s ) ∣ ( s = j Ω ) |H_a(j\Omega)|^2=H_a(j\Omega)H_a^*(j\Omega)=H_a(j\Omega)H_a(-j\Omega)=H_a(s)H_a(-s)|_{(s=j\Omega)} ∣Ha(jΩ)∣2=Ha(jΩ)Ha∗(jΩ)=Ha(jΩ)Ha(−jΩ)=Ha(s)Ha(−s)∣(s=jΩ) , H a ( j Ω ) H_a(j\Omega) Ha(jΩ)可以看做模拟滤波器单位冲激响应的傅里叶变化。
H a ( s ) H_a(s) Ha(s)和 H a ( − s ) H_a(-s) Ha(−s)的零极点对称,成对出现,且其零极点分别分布在左半平面(只有分布在左半平面系统才是稳定的)和右半平面。
巴特沃斯低通逼近
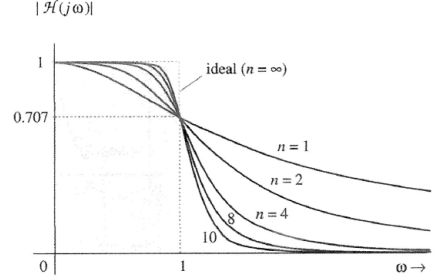
幅度平方函数为 ∣ H a ( j Ω ) ∣ 2 = 1 1 + ( Ω Ω c ) 2 N |H_a(j\Omega)|^2 = \frac{1}{1+(\frac{\Omega}{\Omega_c})^{2N}} ∣Ha(jΩ)∣2=1+(ΩcΩ)2N1 ,其中N为滤波器阶数, Ω c \Omega_c Ωc为3dB截止频率,因为 Ω = Ω c \Omega=\Omega_c Ω=Ωc时,幅度为原来的 1 2 \frac{1}{\sqrt{2}} 21,
-
极点分布
∣ H a ( j Ω ) ∣ Ω = s j 2 = H a ( s ) H a ( − s ) = 1 1 + ( s j Ω ) 2 N |H_a(j\Omega)|_{\Omega=\frac{s}{j}}^2 = H_a(s)H_a(-s) = \frac{1}{1+(\frac{s}{j\Omega})^{2N}} ∣Ha(jΩ)∣Ω=js2=Ha(s)Ha(−s)=1+(jΩs)2N1 ,令 1 + ( s j Ω ) 2 N = 0 1+(\frac{s}{j\Omega})^{2N}=0 1+(jΩs)2N=0即可解得极点分布。
极点在s平面呈象限对称,个数为2N,极点间角度间隔为 π N \frac{\pi}{N} Nπ,极点不落在虚轴上,若N为奇数,实轴上有极点;若为偶数,实轴上无极点。
- 滤波器的系统函数
H a ( s ) = Ω c N ∏ k = 1 N ( s − s k ) H_a(s)=\frac{\Omega_c^N}{\prod_{k=1}^N(s-s_k)} Ha(s)=∏k=1N(s−sk)ΩcN,sk为左半平面的极点。若令 Ω c = 1 r a d / s \Omega_c=1rad/s Ωc=1rad/s,得到的各个阶次的系统函数为归一化的系统函数 H a n ( s ) H_{an}(s) Han(s),其与原系统函数之间的关系为 H a ( s ) = H a n ( s ) ∣ s = s Ω c H_a(s)=H_{an}(s)|_{s=\frac{s}{\Omega_c}} Ha(s)=Han(s)∣s=Ωcs(去归一化)。
- 如何确定N和 Ω c \Omega_c Ωc
已知技术指标: Ω c ( 通 带 截 止 频 率 ) 、 δ 1 ( 通 带 内 允 许 的 最 大 衰 减 ) 、 Ω s ( 阻 带 截 止 频 率 ) 、 δ 2 ( 阻 带 允 许 的 最 小 衰 减 ) \Omega_c(通带截止频率)、\delta_1(通带内允许的最大衰减)、\Omega_s(阻带截止频率)、\delta_2(阻带允许的最小衰减) Ωc(通带截止频率)、δ1(通带内允许的最大衰减)、Ωs(阻带截止频率)、δ2(阻带允许的最小衰减).
δ 1 = − 20 l g ∣ H a ( j Ω ) ∣ , ∣ H a ( j Ω ) ∣ 2 = 1 1 + ( Ω p Ω c ) 2 N → 1 + ( Ω p Ω c ) 2 N = 1 0 0.1 δ 1 → N \delta_1=-20lg|H_a(j\Omega)|,|H_a(j\Omega)|^2=\frac{1}{1+(\frac{\Omega_p}{\Omega_c})^{2N}}\rightarrow1+(\frac{\Omega_p}{\Omega_c})^{2N}=10^{0.1\delta_1}\rightarrow N δ1=−20lg∣Ha(jΩ)∣,∣Ha(jΩ)∣2=1+(ΩcΩp)2N1→1+(ΩcΩp)2N=100.1δ1→N ①
同理,有 1 + ( Ω s Ω c ) 2 N = 1 0 0.1 δ 2 1+(\frac{\Omega_s}{\Omega_c})^{2N}=10^{0.1\delta_2} 1+(ΩcΩs)2N=100.1δ2 ② 由这两个方程可以解得N和 Ω c \Omega_c Ωc 。
Ω c \Omega_c Ωc既可以若由第一个方程解得,那么等同于将通带的技术指标卡死,表示阻带指标有富余,若由第二个方程解得,则与前一种情况相反。
- MATLAB仿真
[N, Wc]=buttord(wp,ws,Rp,Rs,'s') %根据性能指标得到巴特沃斯滤波器的阶数及截止频率
[z,p,k]=buttap(N) %返回N阶归一化原型模拟滤波器的零极点以及增益
[B,A]=zp2tf(z,p,k) %根据零极点增益得到原型多项式的系数(归一化)
[Bt,At]=lp2lp(B,A,Wo) %得到模拟低通滤波器的多项式系数(去归一化)
[BZ,AZ]=bilinear(Bt,At,Fs) %使用双线性变换法求得数字低通滤波器额的多项式系数
切比雪夫低通逼近
-
类型
I型:通带范围内波动;II型:阻带范围内波动。
相比于巴特沃斯:巴特沃斯在整个频带内都是下降的,卡死通带或阻带中其中一个,都将引起另一个的快速变化。 -
幅度平方函数(以I型为例)
∣ H a ( j Ω ) ∣ 2 = 1 1 + ε 2 C N 2 ( Ω Ω c ) |H_a(j\Omega)|^2=\frac{1}{1+\varepsilon^2C_N^2(\frac{\Omega}{\Omega_c})} ∣Ha(jΩ)∣2=1+ε2CN2(ΩcΩ)1
ε : \varepsilon: ε:通带波纹大小, 0 < ε < 1 , 0<\varepsilon<1, 0<ε<1,值越大,波纹越大
Ω c : \Omega_c: Ωc:通带截止频率,不一定为3dB带宽
N : N: N:滤波器阶数
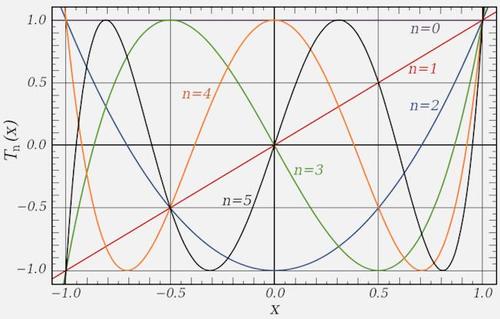
C N ( x ) : C_N(x): CN(x):N阶切比雪夫多项式C N ( x ) = { cos ( N cos − 1 x ) |x|<=1 c h ( N c h − 1 x ) ∣ x ∣ > 1 C_N(x)=\begin{cases} \cos(N\cos^{-1}x)& \text{|x|<=1}\\ ch(Nch^{-1}x)&|x|>1 \end{cases} CN(x)={cos(Ncos−1x)ch(Nch−1x)|x|<=1∣x∣>1,该多项式的图像如下:
从图像可以看出,n为奇数时, ∣ C N ( 0 ) ∣ = 0 |C_N(0)|=0 ∣CN(0)∣=0;n为偶数时, ∣ C N ( 0 ) ∣ = 1 |C_N(0)|=1 ∣CN(0)∣=1。
Ω = Ω c 时 , ∣ C N ( x ) ∣ = 1 , ∣ H a ( j Ω ) ∣ = 1 1 + ε 2 \Omega=\Omega_c时,|C_N(x)|=1,|H_a(j\Omega)|=\frac{1}{\sqrt{1+\varepsilon^2}} Ω=Ωc时,∣CN(x)∣=1,∣Ha(jΩ)∣=1+ε21
在 ∣ x ∣ < = 1 时 , ∣ C N ( x ) ∣ 在 0 − 1 在|x|<=1时,|C_N(x)|在0-1 在∣x∣<=1时,∣CN(x)∣在0−1间反复变化,导致 ∣ H a ( j Ω ) ∣ 在 1 1 + ε 2 |H_a(j\Omega)|在\frac{1}{\sqrt{1+\varepsilon^2}} ∣Ha(jΩ)∣在1+ε21之间反复变化,从而形成波纹$ 。
而 而 而\delta_1 表 示 通 带 内 允 许 的 最 大 衰 减 , 故 应 有 表示通带内允许的最大衰减,故应有 表示通带内允许的最大衰减,故应有\delta_1=20lg\sqrt{1+\varepsilon^2}, 从 而 可 以 解 得 参 数 从而可以解得参数 从而可以解得参数\varepsilon。$
再将阻带允许的最小衰减和阻带截止频率带入即可得到阶数N。 -
极点分布
极点个数为2N个,分布在椭圆上。 -
设计步骤
确定技术指标: Ω p ( = Ω c ) , δ 1 , Ω s , δ 2 \Omega_p(=\Omega_c),\delta_1,\Omega_s,\delta_2 Ωp(=Ωc),δ1,Ωs,δ2
根据技术指标求出滤波器阶数N以及 ε \varepsilon ε: N > = c h − 1 ( k 1 − 1 ) c h − 1 λ s N>=\frac{ch^{-1}(k_1^{-1})}{ch^{-1}\lambda_s} N>=ch−1λsch−1(k1−1), ε 2 = 1 0 0.1 δ − 1 \varepsilon^2=10^{0.1\delta}-1 ε2=100.1δ−1,其中 k 1 − 1 = 1 0 0.1 δ 2 − 1 1 0 0.1 δ 1 − 1 k_1^{-1}=\sqrt{\frac{10^{0.1\delta_2-1}}{10^{0.1\delta_1-1}}} k1−1=100.1δ1−1100.1δ2−1 。
由N和 δ 1 \delta_1 δ1,直接查表得到归一化的系统函数 H a n ( s ) H_{an}(s) Han(s)。
去归一化。 -
MATLAB仿真
[N,Wc]=cheblord(wp,ws,Rp,Rs,'s') %根据性能指标求出切比雪夫滤波器的阶数和截止频率 [z,p,k]=cheb1ap(N,rp) %返回N阶归一化原型模拟滤波器的零极点及增益 [B,A]=zp2tf(z,p,k) %求出归一化低通原型多项式系数 [Bt,At]=lp2lp(B,A,Wo) %求出模拟低通滤波器的系数 [BZ,AZ]=impinvar(Bt,At,Fs) %冲激响应不变法求数字低通滤波器的系数
频率变换法
- 为什么需要频率变换法?
之间的设计方法都是基于低通滤波器进行设计的,为了得到其他类型的滤波器,需要进行频率变换
模拟域频带变换法
- 变换步骤
归一化模拟低通滤波器 ⇒ \Rightarrow ⇒模拟域频带变换 ⇒ \Rightarrow ⇒模拟低通、高通、带通、带阻滤波器 ⇒ \Rightarrow ⇒双线性变换 ⇒ \Rightarrow ⇒数字低通、高通、带通、带阻滤波器。
总结来讲,就是在模拟域就进行频带变换。 - 具体方法
归一化低通滤波器的系统函数: H a ( s ) , s = σ + j Ω H_a(s),s=\sigma+j\Omega Ha(s),s=σ+jΩ
频带变换后的系统函数: H ‾ s ( s ‾ ) , s ‾ = σ ‾ + j Ω ‾ \overline{H}_s(\overline{s}),\overline{s}=\overline{\sigma}+j\overline{\Omega} Hs(s),s=σ+jΩ- 模拟低通 → \rightarrow →模拟低通
s = Ω c s ‾ Ω c ‾ s=\frac{\Omega_c\overline{s}}{\overline{\Omega_c}} s=ΩcΩcs,当 Ω c = 1 \Omega_c=1 Ωc=1时,相当于去归一化。
对应的MATLAB函数为[Bt,At]=lp2lp(B,A,Wo) - 模拟低通 → \rightarrow →模拟带通
s = s ‾ 2 + Ω ‾ 0 2 s ‾ s=\frac{\overline{s}^2+\overline{\Omega}_0^2}{\overline{s}} s=ss2+Ω02, Ω ‾ 0 \overline{\Omega}_0 Ω0为带通滤波器的中心频率, Ω ‾ 0 = Ω ‾ 1 Ω ‾ 2 \overline{\Omega}_0=\overline{\Omega}_1\overline{\Omega}_2 Ω0=Ω1Ω2。 Ω ‾ 1 、 Ω ‾ 2 \overline{\Omega}_1、\overline{\Omega}_2 Ω1、Ω2分别为带通滤波器的上通带截止频率和下通带截止频率。为了得到归一化的带通滤波器,可令 s = s ‾ 2 + Ω ‾ 0 2 s ‾ s=\frac{\overline{s}^2+\overline{\Omega}_0^2}{\overline{s}} s=ss2+Ω02两边同时除以 Ω c ( B ) \Omega_c(B) Ωc(B).
对应的MATLAB函数为[Bt,At]=lp2bp(B,A,Wo,Bw),Bw为带宽。
数字带通滤波器性能指标 → \rightarrow →模拟带通滤波器性能能指标 → \rightarrow →归一化 → \rightarrow →模拟低通滤波器归一化性能指标 → \rightarrow →模拟低通滤波器。
带通滤波器归一化频率计算方法: η = Ω ‾ B \eta=\frac{\overline{\Omega}}{B} η=BΩ
低通滤波器归一化频率计算方法: λ = Ω Ω c , Ω c \lambda=\frac{\Omega}{\Omega_c},\Omega_c λ=ΩcΩ,Ωc为通带截止频率。
两者间关系: λ = η 2 − η 0 2 η \lambda=\frac{\eta^2-\eta_0^2}{\eta} λ=ηη2−η02。
- 模拟低通 → \rightarrow →模拟低通
数字域频带变换法
- 变换步骤
归一化模拟低通滤波器 ⇒ \Rightarrow ⇒数字低通滤波器 ⇒ \Rightarrow ⇒数字域频带变换 ⇒ \Rightarrow ⇒数字低通、高通、带通、带阻滤波器。
总结来讲,就是在数字域进行频带变换。 - 具体方法
低通数字滤波器的系统函数: H L ( z ) H_L(z) HL(z)
频带变化后的数字滤波器的系统函数: H d ( Z ) Hd(Z) Hd(Z)
要求:KaTeX parse error: \tag works only in display equations两个系统函数的单位圆要对应;KaTeX parse error: \tag works only in display equations 都是因果稳定;
关系: H d ( Z ) = H L ( z ) ∣ z − 1 = G ( Z − 1 ) H_d(Z)=H_L(z)|_{z^{-1}=G(Z^{-1})} Hd(Z)=HL(z)∣z−1=G(Z−1) ( G ( Z − 1 ) = ± ∏ k = 1 N Z − 1 − a ∗ 1 − a k Z − 1 G(Z^{-1})=\pm\prod_{k=1}^N\frac{Z^{-1}-a^*}{1-a_kZ^{-1}} G(Z−1)=±∏k=1N1−akZ−1Z−1−a∗(全通函数)应为有理函数)-
数字低通 → \rightarrow →数字低通
N = 1 , z − 1 = G ( Z − 1 ) = Z − 1 − α 1 − α Z − 1 N=1,z^{-1}=G(Z^{-1})=\frac{Z^{-1}-\alpha}{1-\alpha Z^{-1}} N=1,z−1=G(Z−1)=1−αZ−1Z−1−α,根据两个低通滤波器的对应关系(技术指标),最终得到 α = sin θ c − ω c 2 sin θ c + ω c 2 \alpha=\frac{\sin\frac{\theta_c-\omega_c}{2}}{\sin\frac{\theta_c+\omega_c}{2}} α=sin2θc+ωcsin2θc−ωc

-
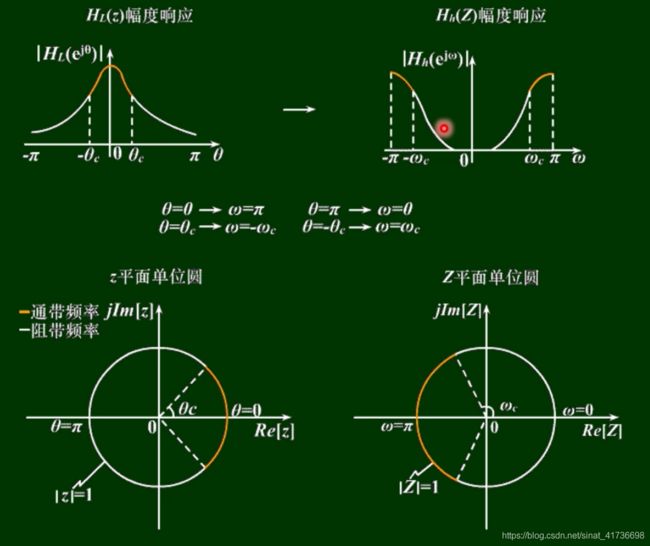
数字低通 → \rightarrow →数字高通
低通频率响应在单位圆上旋转 18 0 ∘ 180^\circ 180∘,即得到高通频率响应:Z=-Z。G ( Z − 1 ) = − Z − 1 − α 1 + α Z − 1 G(Z^{-1})=\frac{-Z^{-1}-\alpha}{1+\alpha Z^{-1}} G(Z−1)=1+αZ−1−Z−1−α
-