数据结构——线性表的查找：顺序查找、设置监视哨的顺序查找、折半查找

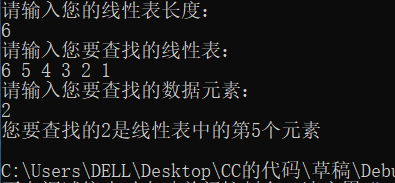
算法7.1顺序查找

#include
using namespace std;

typedef int KeyType;
typedef int InfoType;
#define MAX 1000

typedef struct {
	KeyType key;
	InfoType otherinfo;
}ElemType;

typedef struct {
	ElemType* R;
	int length;
}SSTable;

int Search_Seq(SSTable ST, KeyType key) {
//在顺序表ST中顺序查找其关键字等于key的数据元素。若找到，则函数值为该元素在表中的位置，否则为0
	for (int i = ST.length; i >= 1; i--)//从后往前找
		if (ST.R[i].key == key) return i;
	return 0;
}

void main() {
	int i, key;
	SSTable t;
	t.R = new ElemType[MAX];
	cout << "请输入您的线性表长度：\n";
	cin >> t.length;
	cout << "请输入您要查找的线性表：\n";
	for (i = 1; i <= t.length; i++) cin >> t.R[i].key;
	cout << "请输入您要查找的数据元素：\n";
	cin >> key;
	if (Search_Seq(t, key))
		cout << "您要查找的" << key << "是线性表中的第" << Search_Seq(t, key)
		<< "个元素\n";
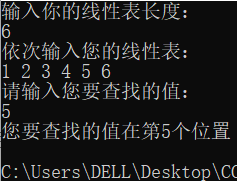
	else cout << "查找失败！\n";
}

算法7.2设置监视哨的顺序查找

#include
#include
using namespace std;

typedef int KeyType;
typedef int InfoType;
#define MAX 100

typedef struct{
	KeyType key;
	InfoType otherinfo;
}ElemType;

typedef struct{
	ElemType *R;
	int length;
}SSTable;

int Search_Seq(SSTable ST,KeyType key){
//在顺序表ST中顺序查找其关键字等于key的数据元素。若找到，则函数值为该元素在表中的位置，否则为0
	int i;
	ST.R[0].key=key;//“哨兵”
	for(i=ST.length;ST.R[i].key!=key;--i);//从后往前找
	return i;
}

void main(){
	int i,key;
	SSTable t;
	t.R=new ElemType[MAX];
	cout<<"请输入您的线性表长度：\n";
	cin>>t.length;
	cout<<"请输入您要查找的线性表：\n";
	for(i=1;i<=t.length;i++) cin>>t.R[i].key;
	cout<<"请输入您要查找的数据元素：\n";
	cin>>key;
	if(Search_Seq(t,key))
		cout<<"您要查找的"<<key<<"是线性表中的第"<<Search_Seq(t,key)
		<<"个元素\n";
	else cout<<"查找失败！\n";
}

算法7.3 折半查找

#include
using namespace std;

typedef int KeyType;
typedef int InfoType;
#define MAX 100

typedef struct {
	KeyType key;
	InfoType otherinfo;
}ElemType;

typedef struct {
	ElemType* R;
	int length;
}SSTable;

int Search_Bin(SSTable ST, KeyType key) {
//在有序表ST中折半查找其关键字key的数据元素。若找到，则该函数值为该元素在表中的位置，否则为0
	int low = 1, high = ST.length, mid;//置查找区间初值
	while (low <= high) {
		mid = (low + high) / 2;
		if (key == ST.R[mid].key) return mid;//找到待查元素
		else if (key < ST.R[mid].key) high = mid - 1;//继续在前一子表进行查找
		else low = mid + 1;//继续在后一子表进行查找
	}
	return 0;//表中不存在元素
}

void main() {
	int i, key;
	SSTable t;
	t.R = new ElemType[MAX];
	cout << "请输入您的线性表长度：\n";
	cin >> t.length;
	cout << "请输入您要查找的线性表：\n";
	for (i = 1; i <= t.length; i++) cin >> t.R[i].key;
	cout << "请输入您要查找的数据元素：\n";
	cin >> key;
	if (Search_Bin(t, key))
		cout << "您要查找的" << key << "是线性表中的第" << Search_Bin(t, key)
		<< "个元素\n";
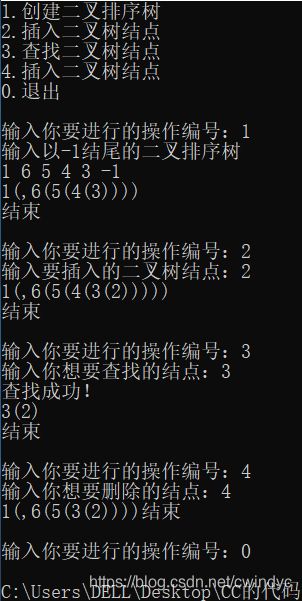
	else cout << "查找失败！\n";
}

二叉排序树的递归查找、插入、创建、删除

#include
using namespace std;

#define MAXN 1000
#define ENDFLAG -1
#define OK 1
#define ERROR 0
typedef int Status;
typedef int KeyType;
typedef int InfoType;

typedef struct {
	KeyType key;
	InfoType otherinfo;
}ElemType;

typedef struct BSTNode {
	ElemType data;
	struct BSTNode* lchild, * rchild;
}BSTNode, * BSTree;

//算法7.4 二叉排序树的递归查找
BSTree SearchBST(BSTree T, KeyType key) {
	if ((!T) || key == T->data.key) return T;
	else if (key < T->data.key) return SearchBST(T->lchild, key);
	else return SearchBST(T->rchild, key);
}

//算法7.5 二叉排序树的插入
void InsertBST(BSTree& T, ElemType e) {
	BSTree S;
	if (!T) {
		S = new BSTNode;
		S->data = e;
		S->lchild = S->rchild = NULL;
		T = S;
	}
	else if (e.key < T->data.key)
		InsertBST(T->lchild, e);
	else if (e.key > T->data.key)
		InsertBST(T->rchild, e);
}

//算法7.6 二叉排序树的创建
void CreateBST(BSTree& T) {
	ElemType e;
	T = NULL;
	cout << "输入以-1结尾的二叉排序树\n";
	cin >> e.key;
	while (e.key != ENDFLAG) {
		InsertBST(T, e);
		cin >> e.key;
	}
}

//算法7.7 二叉排序树的删除
void DeleteBST(BSTree& T, KeyType key) {
	BSTree p = T, f = NULL, q = NULL, s = NULL;
	while (p) {
		if (p->data.key == key) break;
		f = p;
		if (p->data.key > key)p = p->lchild;
		else p = p->rchild;
	}
	if (!p) return;
	if ((p->lchild) && (p->rchild)) {
		q = p;
		s = p->rchild;
		while (s->rchild) {
			q = s;
			s = s->rchild;
		}
		p->data = s->data;
		if (q != p) q->rchild = s->lchild;
		else q->lchild = s->lchild;
		delete s;
		return;
	}
	else if (!p->rchild) {
		q = p;
		p = p->lchild;
	}
	else if (!p->lchild) {
		q = p;
		p = p->rchild;
	}
	if (!f) T = p;
	else if (q == f->lchild) f->lchild = p;
	else f->rchild = p;
	delete q;
}

void PrintBST(BSTree T) {
	if (T == NULL) return;
	else {
		cout << T->data.key;
		if (T->lchild != NULL || T->rchild != NULL) {
			cout << "(";
			PrintBST(T->lchild);
			if (T->rchild != NULL)
				cout << ",";
			PrintBST(T->rchild);
			cout << ")";
		}
	}
}
int main() {
	BSTree T = NULL;
	ElemType e;
	int n, key;
	cout << "1.创建二叉排序树\n";
	cout << "2.插入二叉树结点\n";
	cout << "3.查找二叉树结点\n";
	cout << "4.插入二叉树结点\n";
	cout << "0.退出\n\n";
	do {
		cout << "输入你要进行的操作编号：";
		cin >> n;
		if (n == 1) {
			CreateBST(T);
			PrintBST(T);
			cout << "结束\n\n";
		}
		if (n == 2) {
			cout << "输入要插入的二叉树结点：";
			cin >> e.key;
			InsertBST(T, e);
			PrintBST(T);
			cout << endl;
			cout << "结束\n\n";
		}
		if (n == 3) {
			BSTree t = NULL;
			cout << "输入你想要查找的结点：";
			cin >> key;
			t = SearchBST(T, key);
			if (t) {
				cout << "查找成功！\n";
				PrintBST(t);
				cout << endl;
			}
			else cout << "查找失败！\n";
			cout << "结束\n\n";
		}
		if (n == 4) {
			cout << "输入你想要删除的结点：";
			cin >> key;
			DeleteBST(T, key);
			PrintBST(T);
			cout << "结束\n\n";
		}
		if (n == 0) return 0;
	} while (n);
	return 0;
}

算法7.10 散列表的查找

#include
#include
using namespace std;

#define MAXN 1005
typedef int Status;
typedef int KeyType;
typedef int InfoType;

//- - - - -开放地址法散列表的储存表示- - - - -
typedef struct {
	KeyType key;
	InfoType otherinfo;
}HashTable[MAXN];

int H_p(int length) {
	for (int i = length; i > 2; i--) {
		int flag = 1;
		for (int j = 2; j <= sqrt(length); j++)
			if (i % j == 0) flag = 0;
		if (flag) return i;
	}
	return 2;
}

int H(int length, KeyType key) {
	return key % H_p(length);
}

//- - - - -算法7.10 散列表的查找- - - - -
int SearchHash(HashTable HT, KeyType key, int length) {
	int H0 = H(length, key), Hi, i;
	if (HT[H0].key == 0) return -1;
	else if (HT[H0].key == key) return H0;
	else {
		for (i = 1; i < length; ++i) {
			Hi = (H0 + i) % length;
			if (HT[Hi].key == 0) return -1;
			else if (HT[Hi].key == key) return Hi;
		}
		return -1;
	}
}

void CreateHash(HashTable& HT, int length) {
	KeyType key = 0;
	memset(&HT, 0, sizeof(HT));
	int H0 = H(length, key), Hi, i;
	cout << "输入以0结尾的哈希表\n";
	do {
		cin >> key;
		if (key == 0) break;
		if (HT[H0].key == 0) HT[H0].key = key;
		else if (HT[H0].key == key) {
			cout << "元素" << HT[H0].key << "重复！\n";
		}
		else {
			int flag = 1;
			for (i = 1; i < length; ++i) {
				Hi = (H0 + i) % length;
				if (HT[Hi].key == 0) {
					HT[Hi].key = key;
					flag = 0;
					break;
				}
				else if (HT[Hi].key == key) {
					cout << "数字" << HT[Hi].key << "重复！\n";
					flag = 0;
					break;
				}
			}
			if (flag) cout << "哈希表已满！\n";
		}
	} while (key);
}

void PrintHash(HashTable HT, int length) {
	cout << "哈希表为：\n";
	for (int i = 0; i < length; i++)
		cout << setw(4) << HT[i].key;
	cout << endl;
}

void main() {
	int length, place;
	HashTable HT;
	KeyType key;
	do {
		cout << "输入哈希表的长度：（输入0结束）";
		cin >> length;
		if (length == 0) break;
		CreateHash(HT, length);
		PrintHash(HT, length);
		do {
			cout << "输入你想查找的元素：（输入0结束）";
			cin >> key;
			if (key == 0) break;
			place = SearchHash(HT, key, length) + 1;
			if (place) cout << "是哈希表第" << place << "个元素\n";
			else cout << "不存在要查找的元素！\n";
		} while (key);
		cout << endl;
	} while (length);
}

（前面三个算法可以合并一下，有兴趣就操作一下。新手怼着书抄的，如果有不严谨的地方，请指点！）