论文笔记:Closing the Loop for Robotic Grasping
Grasping Unknown Objects
Closed-Loop Grasping
Visual Servoing
Advantages
- Adapt to dynamic environments
- Not necessarily require fully accurate camera calibration or position control
Drawback
Typically rely on hand-crafted image features for object detection or object pose estimation, so do not perform any online grasp synthesis but instead converge to a pre-determined goal pose and are not applicable to unknown objects.
CNN-based controllers for grasping
Combine deep learning with closed loop grasping
Both systems learn controllers which map potential control commands to the expected quality of or distance to a
grasp after execution of the control, requiring many potential commands to be sampled at each time step.
Benchmarking for Robotic Grasping
3.Grasp point definition
Let g = ( p , φ , w , q ) g = (p,φ, w, q) g=(p,φ,w,q) define a grasp, executed perpendictular to the x-y plane
The gripper’s centre position p = ( x , y , z ) p = (x, y, z) p=(x,y,z) in Cartesian coordinates
The gripper’s rotation φ (around the z axis)
The gripper width w
A scalar quality measure q, representing the chances of grasp success
Detect grasps given a 2.5D depth image I = R H ∗ W I = R^{H * W} I=RH∗W
In the image I a grasp is described by
g̃ = (s, φ̃, w̃, q)
s = (u, v) the centre point in image coordinates
ϕ \phi ϕ is the rotation in the camera’s reference frame
w̃ is the grasp width in image coordinates
A grasp in the image space g̃ ---->converted to-----> a grasp in world coordinates g by applying a sequence of known transforms
g = t R C ( t C I ( g ~ ) ) ( 1 ) g = t_{RC}(t_{CI}(g̃)) (1) g=tRC(tCI(g~))(1)
t R C t_{RC} tRC transforms from the camera frame to the world/robot frame
t C I t_{CI} tCI transforms from 2D image coordinates to the 3D camera frame
Grasp map
The set of grasps in the image space
G = ( ϕ , W , Q ) ∈ R 3 × H × W G = (\phi,W,Q) \in R^{3×H×W} G=(ϕ,W,Q)∈R3×H×W
ϕ \phi ϕ,W,Q are each R 3 × H × W R^{3×H×W} R3×H×W and contain values of φ̃, w̃ and q respectively at each pixel s
Wish to directly calculate a grasp g̃ for each pixel in the depth image I, define a function M from a depth image to the grasp map in the image coordinates
M ( I ) = G M(I) = G M(I)=G
From G can calculate the best visible grasp in the image space g ~ ∗ = m a x Q G g̃^∗ = max_QG g~∗=maxQG, and calculate the equivalent Q best grasp in world coordinates g ∗ g^∗ g∗ via Eq. (1).
G ----------> g̃ -----------> g
4.Generative grasping convolutional neural network
Propose a neural network to approximate the complex function $ M: I \to G$
M θ M_{\theta} Mθ denotes a neural network with \(\theta\) being the weights of the network.
( M θ ( I ) = ( Q θ , ϕ θ , W θ ) ≈ M ( I ) (M_{\theta}(I) = (Q_{\theta},\phi_{\theta},W_{\theta}) \approx M(I) (Mθ(I)=(Qθ,ϕθ,Wθ)≈M(I)
L2 Loss
θ = a r g m i n θ L ( G T , M θ ( I T ) ) \theta = \underset{\theta}{\mathrm{argmin}}L(G_T,M_{\theta}(I_T)) θ=θargminL(GT,Mθ(IT))
A.Grasp representation
Q: quality, at point (u,v),range [ 0 , 1 ] [0,1] [0,1], 1—>higer change
ϕ \phi ϕ: angle, range [ − π 2 , π 2 ] [-\frac{\pi}{2},\frac{\pi}{2}] [−2π,2π]
W: range [ 0 , 150 ] [0,150] [0,150] pixels
B.Training Dataset
C.Network Architecture
D.Training
5.Experimental Set-up
A.Physical Components
- Limitations
Camera: is unable to produce accurate depth measurements from a distance closer than 150mm
Unable to provide any valid depth data on many black or reflective objects.
Gripper: has a maximum stroke of 175 mm
Objects with a height less than 15 mm (especially those that are cylindrical, like a thin pen) cannot be grasped.
B.Test Objects
C.Grasp detection pipeline
Three stages:
- Image processing
- Evaluation of the GG-CNN
- Computation of a grasp pose
The depth image is first cropped to a square, and scaled to 300×300 pixels to suit the input of the GG-CNN.
GG-CNN produce the grasp map \(G_\theta\)
filter \(Q_\theta\) with a Gaussian kernel
Best grasp pose in the image space \(g̃_{\theta}^*\) …
D.Grasp Excution
Two grasping method
- An open-loop grasping method
- A closed-loop
P:There may be multiple similarly-ranked good quality grasps in an image, so to avoid rapidly switching between them
A: Compute three grasps from the highest local maxima of \(G_\theta\) and select the one which is closest (in image coordinates) to the grasp used on the previous iteration.
Initialised to track the global maxima of \(Q_\theta\) at the beginning of each grasp attempt.
E.Object placement
6.Experiments
- Grasping on singulated, static objects from our two object sets
- Evaluate grasping on objects which are moved during the grasp attempt
- Show system’s ability to generalise to dynamic cluttered scenes by reproducing the experiments from [32] and show improved results
- Further show the advantage of our closed-loop grasping method over open-loop grasping by performing grasps in the presence of simulated kinematic errors of our robot’s control.
Static Grasping
Dynamic Grasping
Dynamic Grasping in Clutter
- Isolated Objects
- Cluttered Objects
- Dynamic Cluttered Objects
Robustness to Control Errors
A major advantage of using a closed-loop controller for grasping is the ability to perform accurate grasps despite inaccurate control.We show this by simulating an inaccurate kinematic model of our robot by introducing a cross-correlation between Cartesian (x, y and z) velocities:
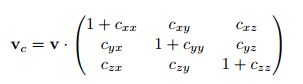
Each \(c ∼ N (0, \sigma^2) \) is sampled at the beginning of each grasp attempt.
Test grasping on both object sets with 10 grasp attempts per object for both the open- and closed-loop methods with \(\sigma = 0.0\) (the baseline case), 0.05, 0.1 and 0.15.
In the case of open-loop controller, where only control velocity for 170 mm in the z direction from the pre-grasp pose, this corresponds to having a robot with an end-effector precision described by a normal distribution with zero mean and standard deviation 0.0, 8.5, 17.0 and 25.5 mm respectively, by the relationship for scalar multiplication of the normal distribution
![]()