自动控制原理中常用的MATLAB函数及操作整理总结
这篇博文是总结性文章,归纳整理了在自控原理课程中经常用到的一些MATLAB函数和操作,包括一些基础操作、分段函数、LORENZ方程、可控可观测转换、生成HILB矩阵等,遇到类似的问题可以直接套用这些模板,最下面是打包的M文件下载地址
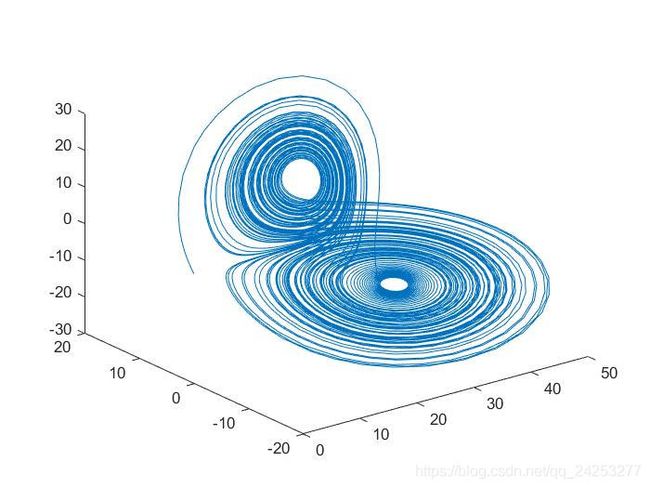
1.LORENZ方程
function [dx]=LORENZ(t,x)
dx=[(-8/3)*x(1)+x(2)*x(3);-10*x(2)+10*x(3);-x(1)*x(2)+28*x(2)-x(3)];
function []=PLOT()
x=[0;0;10^-3];
[t,y]=ode45('LORENZ',[0,100],x);
plot(t,y)
figure;plot3(y(:,1),y(:,2),y(:,3))2.基础操作
2.1Gram判断可控
>> s=tf('s')
>> G=(0.2*(s+2))/(s*(s+0.5)*(s+0.8)*(s+3)+0.2*(s+2))
Transfer function:
0.2 s + 0.4
-------------------------------------
s^4 + 4.3 s^3 + 4.3 s^2 + 1.4 s + 0.4
>> Lc=gram(ss(G),'c')
Lc =
0.0081 -0.0000 -0.0212 0.0000
-0.0000 0.0423 -0.0000 -0.2601
-0.0212 -0.0000 0.5203 0.0000
0.0000 -0.2601 0.0000 5.16942.2Jordan标准型
>> A=[1 2 3 4;5 6 7 8; 9 10 11 12;13 14 15 16];
>> B=[1 2;3 4;5 6;7 8];
>> C=[1 2 3 4;5 6 7 8];
>> D=zeros(2,2);
>> G=ss(A,B,C,D,'InputDelay',0.3,'OutputDelay',0.5)
>> [G1,T]=canon(G,'modal')
a =
x1 x2 x3 x4
x1 36.21 0 0 0
x2 0 -2.209 0 0
x3 0 0 -2.565e-015 0
x4 0 0 0 -2.036e-016
b =
u1 u2
x1 -8.991 -11.09
x2 -0.4937 0.4446
x3 -2.191e-015 -3.232e-015
x4 8.24e-016 1.411e-016
c =
x1 x2 x3 x4
y1 -5.473 -1.606 0 -4.441e-016
y2 -12.65 -0.6257 2.22e-015 0
d =
u1 u2
y1 0 0
y2 0 0
Input delays (listed by channel): 0.3 0.3
Output delays (listed by channel): 0.5 0.5
Continuous-time model.
T =
-0.4385 -0.4966 -0.5546 -0.6127
0.8716 0.4469 0.0222 -0.4025
0.6100 -0.8738 -0.0824 0.3462
-0.3503 0.0899 0.8710 -0.6106
2.3PID负反馈
>> s=tf('s');
>> G=10/(s+1)^3;
>> GC=0.48*(1+1/1.814*s+0.4353*s/(1+0.04353*s));
>> H=1;
>> GG=feedback(G*GC,H)
GG =
0.1152 s^2 + 4.944 s + 4.8
---------------------------------------------------
0.04353 s^4 + 1.131 s^3 + 3.246 s^2 + 7.988 s + 5.82.4TUSTIN变换
>> s=tf('s');
>> G=1/(s+2)^3;
>> G.ioDelay=2
>> G2=c2d(G,0.1,'tustin')
Transfer function:
9.391e-005 z^3 + 0.0002817 z^2 + 0.0002817 z + 9.391e-005
z^(-20) * ---------------------------------------------------------
z^3 - 2.455 z^2 + 2.008 z - 0.5477
Sampling time: 0.12.5传递函数转状态
>> g11=tf(1,[1 2 3],'iodelay',0.5);
>> g12=tf(3,[4 5 6],'iodelay',0.3);
>> g21=tf(4,[7 8 9],'iodelay',0.15);
>> g22=tf(4,[7 8 9],'iodelay',0.15);
>> G=[g11 g12;g21 g22]
>> G1=ss(G)
a =
x1 x2 x3 x4 x5 x6
x1 -2 -1.5 0 0 0 0
x2 2 0 0 0 0 0
x3 0 0 -1.25 -0.75 0 0
x4 0 0 2 0 0 0
x5 0 0 0 0 0 -1.286
x6 0 0 0 0 1 -1.143
b =
u1 u2
x1 0.5 0
x2 0 0
x3 0 0.5
x4 0 0
x5 0.5714 0.5714
x6 0 0
c =
x1 x2 x3 x4 x5 x6
y1 0 1 0 0.75 0 0
y2 0 0 0 0 0 1
d =
u1 u2
y1 0 0
y2 0 0
Input delays (listed by channel): 0.15 0.15
Output delays (listed by channel): 0.15 0
I/O delays:
0.2000 0
0 02.6传递函数-定义算子方式
>> s=tf('s');
>> G=3*(s^2+3)/(s+2)^3*(s^2+2*s+1)*(s^2+5)
G =
3 s^6 + 6 s^5 + 27 s^4 + 48 s^3 + 69 s^2 + 90 s + 45
----------------------------------------------------
s^3 + 6 s^2 + 12 s + 82.7传递函数-系数方式
>> num=[1,2,3];
>> den=[3,2,1];
>> G=tf(num,den)
G =
s^2 + 2 s + 3
---------------
3 s^2 + 2 s + 12.8传递函数矩阵
>> g11=tf(1,[1 2 3],'iodelay',0.5);
>> g12=tf(3,[4 5 6],'iodelay',0.3);
>> g21=tf(4,[7 8 9],'iodelay',0.15);
>> g22=tf(4,[7 8 9],'iodelay',0.15);
>> G=[g11 g12;g21 g22]
G =
From input 1 to output...
1
1: exp(-0.5*s) * -------------
s^2 + 2 s + 3
4
2: exp(-0.15*s) * ---------------
7 s^2 + 8 s + 9
From input 2 to output...
3
1: exp(-0.3*s) * ---------------
4 s^2 + 5 s + 6
4
2: exp(-0.15*s) * ---------------
7 s^2 + 8 s + 92.9传递函数延时
>> s=tf('s');
>> G=1/(s+2)^3;
>> G.ioDelay=2
Transfer function:
1
exp(-2*s) * ----------------------
s^3 + 6 s^2 + 12 s + 82.10画NyBoNi三种图
g11=tf([0.806 0.264],[1 1.15 .202]);
g12=tf([-15 -1.42],[1 12.8 13.6 2.36]);
g21=tf([1.95 2.12 .49],[1 9.15 9.39 1.62]);
g22=tf([7.15 25.8 9.35],[1 20.8 116.4 111.6 18.8]);
G=[g11,g12;g21,g22];
nyquist(G)
figure,bode(G)
figure,nichols(G)2.11矩阵求逆和特征值
>> inv(A)
>> [V,D]=eig(A)
2.12矩阵输入
>> A=[1 2 3 4;4 3 2 1;2 3 4 1;3 2 4 1]
A =
1 2 3 4
4 3 2 1
2 3 4 1
3 2 4 12.13均衡实现
G必须是稳定的才能用
>> [Gb,g,T]=balreal(G)2.14离散传递函数
>> num=[6 -0.6 -0.12];
>> den=[1 -1 0.25 0.25 -0.125];
>> H=tf(num,den,'Ts',0.1)
H =
6 z^2 - 0.6 z - 0.12
-------------------------------------
z^4 - z^3 + 0.25 z^2 + 0.25 z - 0.125
Sample time: 0.1 seconds2.15离散稳定判断
>> num=[6 -0.6 -0.12];
den=[1 -1 0.25 0.25 -0.125];
H=tf(num,den,'Ts',0.1)
Transfer function:
6 z^2 - 0.6 z - 0.12
-------------------------------------
z^4 - z^3 + 0.25 z^2 + 0.25 z - 0.125
Sampling time: 0.1
>> pzmap(H)
>> abs(eig(H))
ans =
0.5000
0.7071
0.7071
0.50002.16离散转连续
>> s=tf('s');
>> G=1/(s+2)^3;
>> G.ioDelay=2
>> G2=c2d(G,0.1,'tustin')
>> D1=d2c(G2)
Transfer function:
9.391e-005 s^3 + 0.003096 s^2 + 0.04542 s + 1.01
exp(-2*s) * ------------------------------------------------
s^3 + 6.02 s^2 + 12.08 s + 8.0812.17连续稳定判断
>> A=[1 2 3 4;5 6 7 8; 9 10 11 12;13 14 15 16];
>> B=[1 2;3 4;5 6;7 8];
>> C=[1 2 3 4;5 6 7 8];
>> D=zeros(2,2);
>> G=ss(A,B,C,D,'InputDelay',0.3,'OutputDelay',0.5)
>> eig(G)
ans =
36.2094
-2.2094
-0.0000
-0.0000
>> pzmap(G)2.18连续转离散
>> g11=tf(1,[1 2 3],'iodelay',0.5);
>> g12=tf(3,[4 5 6],'iodelay',0.3);
>> g21=tf(4,[7 8 9],'iodelay',0.15);
>> g22=tf(4,[7 8 9],'iodelay',0.15);
>> G=[g11 g12;g21 g22]
>> T=0.1;
>> Gd=c2d(G,T)
Transfer function from input 1 to output...
0.004671 z + 0.00437
#1: z^(-5) * ----------------------
z^2 - 1.792 z + 0.8187
0.0007007 z^2 + 0.004044 z + 0.0006493
#2: z^(-1) * --------------------------------------
z^3 - 1.88 z^2 + 0.892 z
Transfer function from input 2 to output...
0.003594 z + 0.003447
#1: z^(-3) * ----------------------
z^2 - 1.868 z + 0.8825
0.0007007 z^2 + 0.004044 z + 0.0006493
#2: z^(-1) * --------------------------------------
z^3 - 1.88 z^2 + 0.892 z
Sampling time: 0.12.19零极点模型
>> P=[-1;-2;-3;-4];
>> Z=[-5;-2+2*i;-2-2*i];
>> G=zpk(Z,P,6)
G =
6 (s+5) (s^2 + 4s + 8)
-----------------------
(s+1) (s+2) (s+3) (s+4)2.20求K值范围
A=[-1.5 -13.5 -13 0;
10 0 0 0;
0 1 0 0;
0 0 1 0];
B=[1;0;0;0];
C=[0 0 0 1];
D=0;
G=ss(A,B,C,D);
rlocus(G)
%k的稳定范围是53.3到4392.21替换变量
>> syms x s;
>> F=x^5+3*x^4+4*x^3+2*x^2+3*x+6;
>> subs(F,x,(s-1)/(s+1))2.22微分方程
>> syms t y;
>> Y=dsolve('D4y+11*D3y+41*D2y+61*Dy+30*y=exp(-6*t)*cos(5*t)','y(0)=1','Dy(0)=1','D2y(0)=0','D3y(0)=0')2.23画响应曲线
>> s=tf('s');
>> G=10/(s+1)^3;
>> GC=0.48*(1+1/1.814*s+0.4353*s/(1+0.04353*s));
>> H=1;
>> GG=feedback(G*GC,H)
>> step(G,10)
>> impulse(G,10)2.24转零极点模型
>> den=[3,2,1];
>> G=tf(num,den)
>> zpk(G)
Zero/pole/gain:
0.33333 (s^2 + 2s + 3)
------------------------
(s^2 + 0.6667s + 0.3333)
2.25状态方程
>> A=[1 2 3 4;5 6 7 8; 9 10 11 12;13 14 15 16];
>> B=[1 2;3 4;5 6;7 8];
>> C=[1 2 3 4;5 6 7 8];
>> D=zeros(2,2);
>> G=ss(A,B,C,D,'InputDelay',0.3,'OutputDelay',0.5)
G =
A =
x1 x2 x3 x4
x1 1 2 3 4
x2 5 6 7 8
x3 9 10 11 12
x4 13 14 15 16
B =
u1 u2
x1 1 2
x2 3 4
x3 5 6
x4 7 8
C =
x1 x2 x3 x4
y1 1 2 3 4
y2 5 6 7 8
D =
u1 u2
y1 0 0
y2 0 0
Input delays (seconds): 0.3 0.3
Output delays (seconds): 0.5 0.52.26状态求传递
>> A=[1 2 3 4;5 6 7 8; 9 10 11 12;13 14 15 16];
>> B=[1 2;3 4;5 6;7 8];
>> C=[1 2 3 4;5 6 7 8];
>> D=zeros(2,2);
>> G=ss(A,B,C,D,'InputDelay',0.3,'OutputDelay',0.5)
>> G1=tf(G)
Transfer function from input 1 to output...
50 s^3 + 80 s^2 - 9.995e-014 s + 5.424e-031
#1: exp(-0.8*s) * -------------------------------------------------
s^4 - 34 s^3 - 80 s^2 - 2.215e-013 s - 4.178e-029
114 s^3 + 240 s^2 - 2.849e-013 s - 1.697e-029
#2: exp(-0.8*s) * -------------------------------------------------
s^4 - 34 s^3 - 80 s^2 - 2.215e-013 s - 4.178e-029
Transfer function from input 2 to output...
60 s^3 + 160 s^2 - 3.202e-013 s - 1.303e-028
#1: exp(-0.8*s) * -------------------------------------------------
s^4 - 34 s^3 - 80 s^2 - 2.215e-013 s - 4.178e-029
140 s^3 + 320 s^2 - 5.892e-013 s - 2.429e-028
#2: exp(-0.8*s) * -------------------------------------------------
s^4 - 34 s^3 - 80 s^2 - 2.215e-013 s - 4.178e-0292.27状态转传递及零极点
>> A=[1 2 3;4 5 6;7 8 9] ;
>> B=[4;3;2];
>> C=[1,2,3];
>> sys=ss(A,B,C,0);
>> tfun=tf(sys)
tfun =
16 s^2 + 72 s + 6.395e-14
-------------------------------
s^3 - 15 s^2 - 18 s + 2.073e-15
Continuous-time transfer function.
>> zpm=zpk(sys)
zpm =
16 s (s+4.5)
---------------------
s (s-16.12) (s+1.117)
Continuous-time zero/pole/gain model.2.28最小化简
>> A=[1 2 3 4;5 6 7 8; 9 10 11 12;13 14 15 16];
>> B=[1 2;3 4;5 6;7 8];
>> C=[1 2 3 4;5 6 7 8];
>> D=zeros(2,2);
>> G=ss(A,B,C,D,'InputDelay',0.3,'OutputDelay',0.5)
>> Gm=minreal(G)
2 states removed.
a =
x1 x2
x1 -1.809 -1.051
x2 -14.47 35.81
b =
u1 u2
x1 -0.2129 0.7221
x2 -9.163 -10.93
c =
x1 x2
y1 0.3611 -5.465
y2 4.101 -12.54
d =
u1 u2
y1 0 0
y2 0 0
Input delays (listed by channel): 0.3 0.3
Output delays (listed by channel): 0.5 0.5
3.可控可观测转换
function Gs=sscanform(G,type)
switch type
case 'ctrl'
G=tf(G);Gs=[];
G.num{1}=G.num{1}/G.den{1}(1);
G.den{1}=G.den{1}/G.den{1}(1);d=G.num{1}(1);
G1=G;G1.ioDelay=0;G1=G1-d;
num=G1.num{1};den=G1.den{1};n=length(G.den{1})-1;
A=[zeros(n-1,1) eye(n-1);-den(end:-1:2)];
B=[zeros(n-1,1);1];C=num(end:-1:2);D=d;
Gs=ss(A,B,C,D,'Ts',G.Ts,'ioDelay',G.ioDelay);
case 'obsv'
Gc=sscanform(G,'ctrl');
Gs=ss(Gc.a',Gc.c',Gc.b',Gc.d','Ts',G.Ts,'ioDelay',G.ioDelay);
otherwise
error('only options "ctrl" and "obsv" are applicable.');
end4.生成Hilb矩阵
function A=myhilb(n, m)
%MYHILB a demonstrative M-function.
% A=MYHILB(N, M) generates an N by M Hilbert matrix A.
% A=MYHILB(N) generates an N by N square Hilbert matrix.
% MYHILB(N,M) displays ONLY the Hilbert matrix, but do not return any
% matrix back to the calling function.
%
%See also: HILB.
% Designed by Professor Dingyu XUE, Northeastern University, PRC
% 5 April, 1995, Last modified by DYX at 21 March, 2000
if nargout>1, error('Too many output arguments.'); end
if nargin==1, m=n;
elseif nargin==0 || nargin>2
error('Wrong number of iutput arguments.');
end
A1=zeros(n,m);
for i=1: n
for j=1:m
A1(i,j)=1/(i+j-2);
end, end
if nargout==1, A=A1; elseif nargout==0, disp(A1); end