"ase_exploration"----一种开源的主动SLAM系统介绍
planning for robotic exploration based on forward simulation
Lauri M, Ritala R. Planning for robotic exploration based on forward simulation[J]. Robotics & Autonomous Systems, 2016, 83(C):15-31.
开源代码:ase_exploration
这篇文章主要介绍了16年的一个active_SLAM论文,文章配套有开源代码
1、 本篇文章将active_SLAM问题看作是一个POMDP(部分可观测的马尔科夫决策过程),所要寻找就是有一个好的目标函数来决定下一步该执行哪一个决策;即在active_SLAM中,我们需要给定每一条候选目标意味着多大的信息增益,需要选一个“预测”信息增益最大的目标点,然后在规划路径(A*,D*,RRT,PRM)。本文的路径候选方法不太一样,同时也是多步预测(non-myopic),下面会做一些详细的介绍。
2、 提出一种新的基于采样的互信息近似方法,在论文中给了严格的推导,分布中包括了机器人的位置姿态序列和最后的地图;但是在实际实现的过程中,位置姿态序列基本上意义不大,从gmapping中直接获取当前位姿信息和map信息。在后续获取reward时,用了传统的栅格地图信息熵的计算方式。
3、 规划方法应该算是本文的一大亮点,并不是传统的从采样点到路径生成的方法,而是直接采样控制命令(线速度和角速度)而后再获取目标点,评价目标点位置的信息增益,因为本文又是多步,所以是多步信息增益累加,再评价,通过粒子滤波和模拟退火(多次观测)。
4、 文章的实验部分也很充分,两个模拟和一个实际实验,对比于frontier_exploration, 以及不同步长的该方法,对比的指标在于探索区域的面积大小。其实还需要更加量化的去表达建图质量和探索区域(比特或者奈特)。这个期刊也比较重视实验过程和实际效果,确实本文比较接地气,实验复杂的多,相比于别的,在目前active_SLAM并没有一个客观的指标:run-time,efficiency,quality and area explored 等等。
5、 论文所提方法已经开源,也有仿真模块。
存在问题:
本文所提算法,得基于多步预测,当环境大体信息已知的情况下会取得较好的效果,具体可以如下图所示;但是这样一来,就丧失了探索的必要性。在具体实现的过程中,也提供了这样的一个选项就是有已知地图,当然也可以没有,其实在后续实验中作者也没采用先验的已知地图。在其他论文的一些介绍中,有通过卷积进行已知空闲区域观测位置的评价,或者是根据边界区域预测landmark的数量,或者去在探索边界区域的时候,评价一下每条路径的信息增益,而不是就近找一条。
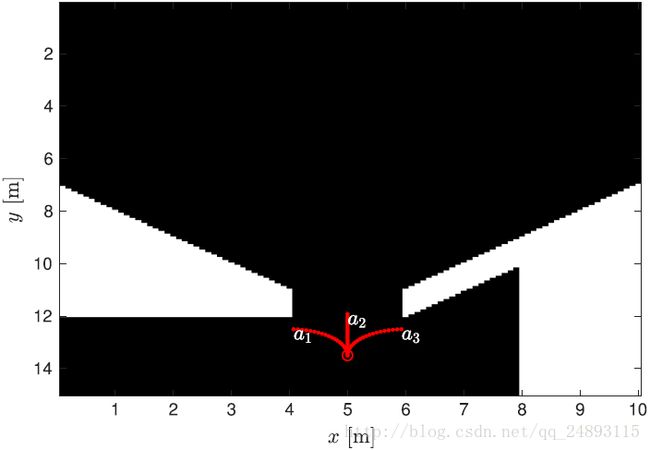
具体的其他方法会在后续博客中进行介绍。
另一个方面就是,虽然在互信息模块,作者采用了非常严密的推导,但是具体也比较难实施,主体的SLAM过程仍然采用gmapping等一些较为成熟的栅格建图方法。也没有从当前位置姿态的不确定度进行考量,只是采用了不同的决策路径使得获得不同的地图信息增益(log-odd)从而决定路径的选择。
细节部分介绍
以POMDP进行探索
在模型完全已知的情况下,该过程即被成为MDP(马尔科夫决策过程),鉴于在active_SLAM的一个模型部分未知或者完全的情况的情况,则需要通过假设和预测获取候选对象的回报值,通过预测得到的回报值进行决策。
1、通过 s∈S 代表系统的隐含状态,包括移动机器人的状态和地图状态;
2、每次控制时刻顺序集, T={0,1,...,H−1},H∈N∪{∞} , H 代表了预测层数(因为本文在考虑之初(non-myopic));
3、控制决策选择: u∈U ,决策执行之后的观测: z∈Z 。
4、在当前系统状态下的概率密度函数, b∈B :
5、马尔科夫的运动状态转移模型: T(s′,s,u) ,观测模型: O(z′,s′,u)
在给定概率密度函数,以及决策动作时,关于预测的先验概率:
在执行决策之后,给一个观测,根据贝叶斯规则,后验概率模型:
在后续回报值的表达方式中,常常将上述后验概率模型表述为如下的函数模型:
关于上述函数,在文章中,给出了这样的变换过程: B×U×Z=B ,从过程上来看,则代表了贝叶斯滤波的过程,原始概率密度函数,经过状态转移,再经过观测更新,得到了新的概率密度函数。
从信息增益的角度来说,不确定性函数(信息熵) f:B→R+ (标量)。而信息增益则表达为如下(前后两次不确定性函数相减):
理想的决策应该使得上述的式子达到最大(在决策空间里),也可以理解为将决策的不确定性函数(环境信息熵)降到最小。通过香农信息论中的互信息概念计算信息增益。
如果把这当作一个POMDP问题,类似于强化学习的过程,则每一步决策 执行的时候,都有个立即回报值: ρ:B×U→R
Q1≡ρ(b,u)
Qt≡ρ(b,u)+γ∫z′∈Zη(z′|b,u)V∗t−1(τ(b,u,z′))dz′
其中: V∗t(b)=supu∈UQt(b,u) ,最优决策回报值;
π∗t(b)=argsupu∈UQt(b,u) ,最优汇报值所对应的决策序列。
使用开环(open-loop)方法处理POMDP问题
使用开环进行处理的话,就意味着未来观测到的信息不会对之前已经做出的决策产生影响,这样的近似方式简化了求解过程,但是损失了一部分最优性。用 b0 表示当前分布, u0:H−1 作为决策序列, z1:H 作为观测序列,具体过程由以下式子表示:
求解最优决策序列的开环目标函数:
从而获取最优决策结果。
前向模拟(Forward simulation)解决开环控制问题:
在前向仿真的模块中,作者将决策序列的可数和不可数分别进行了讨论,在实际实验和代码中作者使用了不可数决策空间的基于蒙特卡洛的序贯重要性(SMC)采样求取最优决策方案;而文章也大篇幅介绍了关于可数空间的蒙特卡洛决策树搜(MCTS),这方面的内容,耳熟能详的就是alpha狗的成功应用。下面是一个SMC算法的流程:

上述伪代码的理论框架,是文章所列文献[44]、[45],这一段内容似懂非懂,但是和后续的理解和代码阅读出入不大。所用的方法是结合了模拟退火和最大似然估计的贝叶斯框架。
算法2可以认为一个传统的带重采样的序贯重要性采样算法,确定迭代次数,确定粒子群规模,不断的迭代收敛,选取一条权重最大的路径(若干的路径点,代码实现中以倒数第二个节点作为目标点,发送给navigation 中的move_base)。
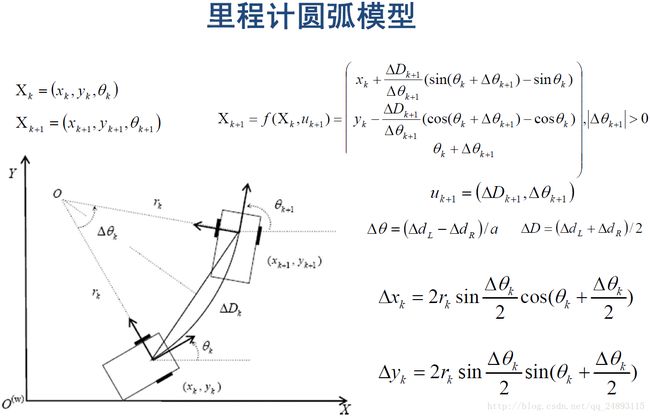
本文区别于其他文献的意义在于,在生成候选路径时,并不是现有目标点,在生成由起始点到目标点的路径;而是先从速度空间采样,第一迭代采样会在速度定义域( vmin∼vmax 与 wmin∼wmax )内进行均匀分布采样,接下来几次迭代则是在则基于上一次粒子对应的速度进行高斯采样(方差随着的迭代次数的增加而逐渐减小),最终通过圆弧运动模型,生成路径节点。下图是圆弧里程计模型:
以下各图是具体采样过程的效果示意图:

上图是初始采样生成的节点路径地图,可以看出这样的路径没有平滑处理,并不适合执行,事实上就算是最后决定下来的路径也不是最后所实施的路径。经过若干次迭代之后,路径逐渐收敛;当粒子多样性小于给定阈值,即需要进行重采样。
算法中,还有个地方得注意,就是模拟退火,认为迭代次数越多,需要退火的时间越长,退火利用多次观测进行表述。
互信息估计(mutual information)
互信息(Mutual Information)是信息论里一种有用的信息度量,它可以看成是一个随机变量中包含的关于另一个随机变量的信息量,或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。在SLAM中,互信息可以认为是观测和状态量之间的互信息,希望通过观测来降低状态(位姿与地图)的不确定性,那么互信息最大就意味本次观测对于降低状态的不确定性贡献越大。

互信息链式规则,其实等同于SLAM过程。
文章中,有这样的一个假设:
机器人运动状态的转移与地图信息的转移是相互独立的,即满足下列式子:
T(s′,s,u)=Tx(x′,x,u)T(m′,m),
其中, Tx(x′,x,u):X×X×U→R+ , T(m′,m):M×M→R+
分别表示状态和地图信息变化,但是这并不意味着两者没有关系,只是在度量信息的时候没有考虑。那么上面公式中的红色项可以简化为:
通过粒子采样的方式,进行下列近似互信息, {x′(i),z′(i)}Ni=1∼p(x′,z′|b,u) 。
虽然模型中是那么推的,但是真的想要获取近似的效果难度可见一斑,首先粒子从后验概率中的采样就很难办到,过多的限制内容在文章会有详细介绍。
上面的式子可以分成关于位姿的互信息,以及关于地图的互信息;在实现具体功能的时候,通过调用SLAM算法(gmapping)获取状态量(位置姿态与地图信息),剩下的部分就是观测与地图互信息的估计,也就是在评价路径(SMC)时所用的权重,因为采用的栅格地图,栅格之间又保持相互独立性,所以地图的信息熵就是按照离散信息熵求解进行的,代码中对于这块的求解按照如下的式子进行:
观测信息预测

上图在预测观测信息中,主要使用的就是bresenham算法,具体内容可参照源码。
有问题可加群 (移动机器人导航与控制群:199938556) 讨论交流,进群修改备注。
