Leetcode刷题总结--单调栈
Leetcode刷题总结
单调栈
从这个数据结构的名字就可以看到,数据在栈中是单调的,栈顶永远都是最大/最小值。
那么,这样一个数据结构有什么用呢?这里作者先把结论说出来,然后举一个例子说明。
寻找每个元素左右距离自己最近且比自己大/小的元素。
假设目前要维护一个单调递增的栈,输入序列为 8,3,1,2,5
(下面的单调性是我自己这样认为的,即单调递增的栈,从栈底到栈顶依次递增,栈顶是最大的。主要是为了说明单调栈的结构特点,当然大家也可以觉得栈底是最大的,只要是单调的就都ok)
-
输入
8时,栈为空,直接入栈,此时栈内元素为 (8)。(注:左侧为栈底部) -
输入
3时,要维护栈为递增的,需要将8弹栈,此时栈为空。弹栈这一步,就包含了一个信息,
8的右边最小元素为3,左边最小元素不存在 -
输入
1时,要维护栈为递增的,需要将3弹栈,此时栈为空。弹栈这一步,就包含了一个信息,
3的右边最小元素为1,左边最小元素不存在 -
输入
2时,不需要弹栈,直接插入,此时栈元素为(1,2)。 -
输入
5时,不需要弹栈,直接插入,此时栈元素为(1,2,5)。 -
最后再将栈元素依次清空时,就可以得到每个元素左边最小的元素,即
5的左边最小值是2,2的左边最小值是1,1的左边最小不存在
通过上述过程,我们可以分析出,因为栈的单调性,使得数据在处理过程中,也拥有了方向性。
元素入栈时,可以判断一侧的信息,出栈时,可以判断另一侧的信息。
伪代码模板:
stack<int> s;
for(int i=0;i<len;i++) // 遍历题目中给定的序列
{
while(!s.empty() && ilegal(s.top(),i)) //当前元素破坏了栈的单调性
{
// 1. 得到栈顶元素;
int tmp = s.top();
// 2. 弹栈,调整
s.pop();
// 3. 进行相信的信息处理
handle(tmp,i);
}
s.push(i); // 当前元素入栈,可以是下标,也可以是元素,也可以是其他东西
}
while(!s.empty()) //对栈内剩余元素进行处理
{
// 1. 得到栈顶元素;
int tmp = s.top();
// 2. 弹栈,调整
s.pop();
// 3. 进行相信的信息处理
handle(tmp,s.top());
}
Leetcode496 下一个更大元素
题目描述:
给定两个 没有重复元素 的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。
示例:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于num1中的数字4,你无法在第二个数组中找到下一个更大的数字,因此输出 -1。
对于num1中的数字1,第二个数组中数字1右边的下一个较大数字是 3。
对于num1中的数字2,第二个数组中没有下一个更大的数字,因此输出 -1。
算法思想
下一个最大元素,也就是右侧最近比自己大的元素,可以使用单调栈来解决。这里让栈的单调性为从栈底到栈顶,元素依次减小,栈顶最小。这样一来在元素入栈的时候,可以找到当前栈顶元素下一个最大元素。最后留在栈内的元素不存在下一个更大元素。根据得到的信息,再根据nums1的顺序给出答案的排列。
算法步骤
-
按顺序将元素入栈,当前元素A比栈顶大,弹出栈顶元素,栈顶元素下一个更大元素为A.
-
将栈清空,此时弹栈元素的下一个更大元素赋值为-1。
-
根据num1中元素出现顺序,构造答案。
(所有数的右侧更大元素均记录在哈希表中,方便构造答案的时候直接查找)
代码
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2)
{
unordered_map<int,int> rightmax;
stack<int> s;
for(int i=0;i<nums2.size();i++)
{
while(!s.empty() && nums2[i]>=nums2[s.top()])
{
int temp = s.top();
s.pop();
rightmax[nums2[temp]] = nums2[i];
}
s.push(i);
}
while(!s.empty())
{
s.pop();
}
vector<int> ans;
for(auto n:nums1)
{
if(rightmax.count(n)==0)
{
ans.push_back(-1);
}
else
{
ans.push_back(rightmax[n]);
}
}
return ans;
}
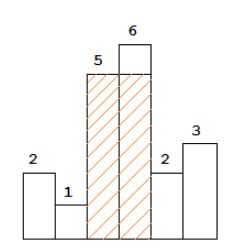
Leetcode84 直方图的最大矩形l
题目描述:
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例:
算法思想:
计算以每个柱状体 i i i为标准,可以左右移动的最大位置 l , r l,r l,r。这样一来,高度为i的矩形面积就是 ( r − l ) ∗ i (r-l)*i (r−l)∗i
这样一来,只需要统计每个柱可以左右移动的最大位置,然后求解每个柱子可以围成的最大面积,取最大值。
如何确定一个柱子能够移动的边界?这个柱子左右的下一个更小的柱子,这就是寻找的边界了
如何求解左右的下一个更小?单调栈
算法步骤:
- 利用单调栈求出每个元素的左右下一个更小
- 计算出面积然后找出最大值
代码:
int largestRectangleArea(vector<int>& matrix)
{
if(matrix.size()==0) return 0;
int len = matrix.size();
vector<int> leftmin(len,-1);
vector<int> rightmin(len,len);
stack<int> s;
for(int i=0;i<len;i++)
{
while(!s.empty() && matrix[i] <= matrix[s.top()] )
{
int k = s.top();
s.pop();
rightmin[k] = i;
}
leftmin[i] = s.empty()?-1:s.top();
s.push(i);
}
while(!s.empty())
{
int k = s.top();
s.pop();
leftmin[k] = s.empty()?-1:s.top();
rightmin[k] = len;
}
int maxsize = 0;
for(int i=0;i<len;i++)
{
maxsize = max(maxsize,(rightmin[i]-leftmin[i]-1)*matrix[i]);
}
return maxsize;
}
Leetcode907 子数组最小值之和
题目描述:
给定一个整数数组 A,找到 min(B) 的总和,其中 B 的范围为 A 的每个(连续)子数组。
由于答案可能很大,因此返回答案模 10^9 + 7。
示例:
输入:[3,1,2,4]
输出:17
解释:
子数组为 [3],[1],[2],[4],[3,1],[1,2],[2,4],[3,1,2],[1,2,4],[3,1,2,4]。
最小值为 3,1,2,4,1,1,2,1,1,1,和为 17。
算法思想:
转换一下思路,当前元素最多可以在多少个子数组里面是最小值?
这样一来,题目有转化成了求解一个元素的左右的下一个更小值,与上一个问题相同了。
假设当前元素 i i i,左侧可以扩展 m m m位,右侧可以扩展 n n n位,那么以 i i i为最小值的子数组数目为 1 + m + n + m ∗ n 1+m+n+m*n 1+m+n+m∗n
那么元素 i i i对答案的贡献就是 ( 1 + m + n + m ∗ n ) ∗ i (1+m+n+m*n)*i (1+m+n+m∗n)∗i
对所有位置都这么计算,把答案相加即可。
int sumSubarrayMins(vector<int>& A) {
const int mod = 1e9 + 7;
int n = A.size();
vector<int> lmin(n, -1);
vector<int> rmin(n, n);
stack<int> stk;
for (int i = 0; i<A.size(); i++)
{
while (stk.size() && A[i] <= A[stk.top()]){
rmin[stk.top()] = i;
stk.pop();
}
if (stk.size()) lmin[i] = stk.top();
stk.push(i);
}
int ans = 0;
for (int i = 0; i< n; i++)
{
int m = i - lmin[i] -1;
int n = rmin[i] - i -1;
int k = 1 + m + n + m * n;
ans += k * A[i];
ans = ans % mod;
}
return ans;
}
Leetcode85 矩形面积
题目描述:
给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
输入:
[
[“1”,“0”,“1”,“0”,“0”],
[“1”,“0”,“1”,“1”,“1”],
[“1”,“1”,“1”,“1”,“1”],
[“1”,“0”,“0”,“1”,“0”]
]
输出: 6
算法思想
这个题是柱状图的最大矩形的一问题的一个变形。如果矩阵的大小是1*n,那么这个题就和84题一模一样了。
如此相似的两个题,在方法上肯定也有共通之处。我们试着将二维矩阵压缩为一维。
对于第一行,["1","0","1","0","0"],存在两个大小为1的矩形
对于前两行,把这两行看成是直方图,可以得到最大矩形面积为3
["1","0","1","0","0"] |
|---|
["1","0","1","1","1"] |
因此,把上一行一行都累加到下一行上,就可以将问题转化为直方图内的最大矩形问题。
(当前位置为0,则不变;当前位置为1,则加上方面累加的数值)
然后,对每一行都使用依次单调栈,找出以当前行为底时的最大矩形,更新最大值
算法步骤:
- 对该行使用单调栈结构,计算最大面积
- 将这一行的元素对应位置累加到下一行,重复步骤1
- 矩阵最后一行遍历结束,返回结果
代码:
int maxArea(vector<char>& matrix)
{
if(matrix.size()==0) return 0;
int len = matrix.size();
int maxarea = 0;
stack<int> s;
for(int i=0;i<len;i++)
{
while(!s.empty() && matrix[i] <= matrix[s.top()])
{
// i就是右边最近的最大值
int j = s.top();
s.pop();
int k = s.empty()?-1:s.top(); //左边最近的最大值
int curArea = (i-k-1)*(matrix[j]-48);
maxarea = max(curArea,maxarea);
}
s.push(i);
}
while(!s.empty())
{
int j = s.top();
s.pop();
int k = s.empty()?-1:s.top();
// 左边界为k,右边界统一为数组的右边
int curArea = (len-k-1)*(matrix[j]-48);
maxarea = max(maxarea,curArea);
}
return maxarea;
}
// 求解矩阵中的最大矩形
int maximalRectangle(vector<vector<char>>& matrix)
{
if(matrix.size() == 0) return 0;
int ans = maxArea(matrix[0]);
int row = matrix.size();
int col = matrix[0].size();
for(int i=1;i<row;i++)
{
for(int j=0;j<col;j++)
{
if(matrix[i][j]!='0')
{
matrix[i][j] += matrix[i-1][j] - 48;
}
}
int tmp = maxArea(matrix[i]);
ans = max(ans,tmp);
}
return ans;
}