BFS题库+详解
BFS
文章目录
- BFS
- 1.逃脱-NC14536 (双bfs)
- 2.after与迷宫-NC14608(两次bfs)
- ①p.s.一开始的错误想法
- ②正确代码
- 3.寻找道路-NC16498【NOIP2014提高组】(图论,附加条件bfs)
- 4.华容道-NC16536【NOIP2013提高组】(bfs+spfa)
1.逃脱-NC14536 (双bfs)
Tabris来到幼儿园的第四天,幼儿园老师在值班的时候突然发现幼儿园某处发生火灾,而且火势蔓延极快,老师在第一时间就发出了警报,位于幼儿园某处的mengxiang000和Tabris听到了火灾警报声的同时拔腿就跑,不知道两人是否能够逃脱险境? 幼儿园可以看成是一个N*M的图,在图中一共包含以下几种元素:
.:表示这是一块空地,是可以随意穿梭的。
#:表示这是一块墙,是不可以走到这上边来的,但是可以被火烧毁。
S:表示mengxiang000和Tabris所在位子。
E:表示幼儿园的出口。
*:表示火灾发源地(保证输入只有一个火灾发源地)。
已知每秒有火的地方都会向周围八个格子(上下左右、左上、右上、左下、右下)蔓延火势.mengxiang000和Tabris每秒都可以选择周围四个格子(上下左右)进行移动。(假设两人这一秒行动完之后,火势才蔓延开) 根据已知条件,判断两人能否成功逃脱险境,如果可以,输出最短逃离时间,否则输出T_T。
输入描述:
第一行输入一个整数t,表示一共的测试数据组数。第二行输入两个整数n,m,表示幼儿园的大小。接下来n行,每行m个字符,表示此格子是什么元素。t<=2003<=n<=303<=M<=30保证图中有一个起点,一个出口,一个火灾源处.为了防止孩子们嬉戏中受伤,墙体是橡胶制作的,可以燃烧的哦。
输出描述:
每组数据输出一行,如果两人能够成功到达出口,那么输出最短逃离时间,否则输出T_T
输入:
3
5 5
…
…
…S#.
…E.
…
5 5
…#
…#S#
…##
…E
…
5 5
…
S…
…*#.
…E.
…
输出:
2
T_T
T_T
思路:
写两个BFS,分别判断是否经过该位置和火灾到达该位置时间
#include
#define loopx(a,b,i) for(int i=a;i<=b;i++)
#define lson (p<<1)
#define rson ((p<<1)|1)
#define mid ((l+r)>>1)
#define MAX 100005
char mapp[50][50];
int d[50][50];//存储是否到达过该位置
int g[50][50];//存储火灾到达此位置时间
int dir[8][2]={1,0,-1,0,0,-1,0,1,1,1,1,-1,-1,1,-1,-1};
int n,m,flag;
struct node
{
int x,y,t;
}now,nex;
queue <node> cot;
int judge(int x,int y)//判断是否越界及是否到达过
{
return x>=1&&x<=n&&y>=1&&y<=m&&d[x][y]==0;
}
int bfsman(int x,int y)//人是否可以走出及最短逃离时间
{
memset(d,0,sizeof(d));
now.x=x;
now.y=y;
now.t=0;
d[x][y]=1;
while(!cot.empty())cot.pop();
cot.push(now);
while(!cot.empty())
{
now=cot.front();
cot.pop();
if(mapp[now.x][now.y]=='E')return now.t;
for(int i=0;i<4;i++)
{
nex.x=now.x+dir[i][0];
nex.y=now.y+dir[i][1];
nex.t=now.t+1;
if(judge(nex.x,nex.y)&&nex.t<g[nex.x][nex.y]&&mapp[nex.x][nex.y]!='#')
{
d[nex.x][nex.y]=1;
cot.push(nex);
}
}
}
return -1;
}
void bfsfire(int x,int y)//火到达此位置的时间
{
memset(d,0,sizeof(d));
memset(g,0,sizeof(g));
now.x=x;
now.y=y;
now.t=0;
d[x][y]=1;
g[x][y]=0;
while(!cot.empty())cot.pop();
cot.push(now);
while(!cot.empty())
{
now=cot.front();
cot.pop();
for(int i=0;i<8;i++)
{
nex.x=now.x+dir[i][0];
nex.y=now.y+dir[i][1];
nex.t=now.t+1;
if(judge(nex.x,nex.y))
{
d[nex.x][nex.y]=1;
cot.push(nex);
if(mapp[nex.x][nex.y]=='E')
g[nex.x][nex.y]=nex.t+1;
else
g[nex.x][nex.y]=nex.t;
}
}
}
}
int main()
{
int t;
int x,y,a,b;
cin>>t;
while(t--)
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin>>mapp[i][j];
if(mapp[i][j]=='S')
{
x=i;y=j;
}
if(mapp[i][j]=='*')
{
a=i;b=j;
}
}
bfsfire(a,b);
int ans=bfsman(x,y);
if(ans!=-1)cout<<ans<<endl;
else cout<<"T_T"<<endl;
}
return 0;
}
2.after与迷宫-NC14608(两次bfs)
after的算法书的遗落在一个叫做AIJ的迷宫中了,这个迷宫有N*M个房间,迷宫的入口为(1,1),算法书遗落在(r,c)。迷宫中的房间有四种状态:空房间、无法进入的房间、有墨菲斯托存在的房间和有莉莉丝存在的房间。墨菲斯托会否定一切,而莉莉丝会诱惑人做一种叫做YK的活动。after是一个意志薄弱的人,他遇到了墨菲斯托和莉莉丝之后,便会变成眼神空洞的超级YK机器人。after每步可以从他当前的房间走至上下左右四个房间的其中一个房间。after害怕变成超级YK机器人,所以要尽快拿到算法书然后从入口逃离。问after最少需要走多少步才可以在不变成超级YK机器人的情况下从入口出发取回算法书并逃离迷宫?
输入描述:
第一行一个正整数T(T<=10),表示共有T组数据。对于每组数据,第一行四个正整数N,M,r,c(1<=N,M<=1000;1<=r<=N;1<=c<=M)。接下来N行,每行M个字符,每个表示房间的状态,“.”表示空房间,“*”表示无法进入的房间,“F”表示有墨菲斯托存在的房间,“M”表示有莉莉丝存在的房间。数据保证(1,1)为“.”。
输出描述:
对每组数据输出一行,即after最少需要走的步数。若after无法取回算法书,则输出“IMPOSSIBLE”(不带引号)。
输入:
1
4 4 4 3
…**
*F…
..
*M.F
输出:
14
思路:
因为一条路不能都有F和M,所以用两个bfs,一个不走M,一个不走F,最后取两个较小值。
①p.s.一开始的错误想法
一开始想着用结构体存储当前这条路是否已经走过F和M,但忽略了bfs会将已经走过的地方标记,如果短的路和长的路有共同的一部分,如果短的路之前有过F,走到共同部分遇到M,那么短的路失效,但是此时公共节点已经标记过,所以长的路就算最终满足条件也走不下去。例如:
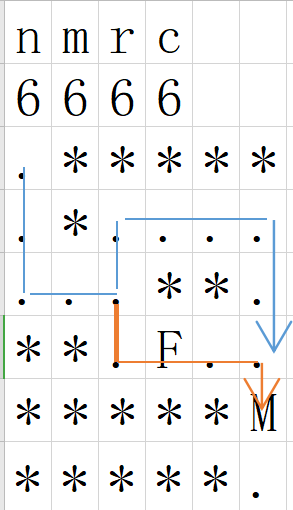
红色路程短但不满足,当红色走到M时不符合题意,但M的前一节点(也就是M上面的点)已标记走过,所以蓝色的路被阻止,题目无解。
#include
#define loopx(a,b,i) for(int i=a;i<=b;i++)
#define lson (p<<1)
#define rson ((p<<1)|1)
#define mid ((l+r)>>1)
#define MAX 100005
char mapp[1005][1005];
int d[1005][1005];
int dir[8][2]={1,0,-1,0,0,-1,0,1,1,1,1,-1,-1,1,-1,-1};
int n,m,r,c;
struct node
{
int x,y;
int f,m;//这条路是否经过过F,M
int ans;
}now,nex;
queue<node>que;
//int judge(struct node no)
//{
// return no.x>=1&&no.x<=n&&no.y>=1&&no.y<=m&&d[no.x][no.y]==0&&mapp[no.x][no.y]!='*'&&(no.f==0||no.m==0);
//}
int bfs(int x,int y)
{
memset(d,0,sizeof(d));
now.x=x;
now.y=y;
now.ans=0;
now.f=0;
now.m=0;
d[x][y]=1;
while(!que.empty())que.pop();
que.push(now);
while(!que.empty())
{
now=que.front();
que.pop();
if(now.x==r&&now.y==c)return now.ans;
for(int i=0;i<4;i++)
{
nex.x=now.x+dir[i][0];
nex.y=now.y+dir[i][1];
nex.ans=now.ans+1;
if(nex.x<1||nex.x>n||nex.y<1||nex.y>m)continue;
if(mapp[nex.x][nex.y]=='*'||d[nex.x][nex.y]==1)continue;
nex.f=now.f;
nex.m=now.m;
if(mapp[nex.x][nex.y]=='F')nex.f=1;
if(mapp[nex.x][nex.y]=='M')nex.m=1;
if(nex.f==1&&nex.m==1)continue;
d[nex.x][nex.y]=1;
que.push(nex);
//cout<
}
}
return -1;
}
int main()
{
int t;
cin>>t;
while(t--)
{
cin>>n>>m>>r>>c;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>mapp[i][j];
int ans=bfs(1,1);
if(ans==-1)cout<<"IMPOSSIBLE"<<endl;
else cout<<ans*2<<endl;
}
return 0;
}
②正确代码
#include
#define loopx(a,b,i) for(int i=a;i<=b;i++)
#define lson (p<<1)
#define rson ((p<<1)|1)
#define mid ((l+r)>>1)
#define MAX 100005
char mapp[1005][1005];
char ma[1005][1005];
int d[1005][1005];
int dir[8][2]={1,0,-1,0,0,-1,0,1,1,1,1,-1,-1,1,-1,-1};
int n,m,r,c;
struct node
{
int x,y;
int ans;
}now,nex;
queue<node>que;
//int judge(struct node no)
//{
// return no.x>=1&&no.x<=n&&no.y>=1&&no.y<=m&&d[no.x][no.y]==0&&mapp[no.x][no.y]!='*'&&(no.f==0||no.m==0);
//}
int bfs(int x,int y)//找到当前图最短路
{
memset(d,0,sizeof(d));
now.x=x;
now.y=y;
now.ans=0;
d[x][y]=1;
while(!que.empty())que.pop();
que.push(now);
while(!que.empty())
{
now=que.front();
que.pop();
if(now.x==r&&now.y==c)return now.ans;
for(int i=0;i<4;i++)
{
nex.x=now.x+dir[i][0];
nex.y=now.y+dir[i][1];
nex.ans=now.ans+1;
if(nex.x<1||nex.x>n||nex.y<1||nex.y>m)continue;
if(ma[nex.x][nex.y]=='*'||d[nex.x][nex.y]==1)continue;
d[nex.x][nex.y]=1;
que.push(nex);
//cout<
}
}
return -1;
}
int main()
{
int t;
cin>>t;
while(t--)
{
cin>>n>>m>>r>>c;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>mapp[i][j];
for(int i=1;i<=n;i++)//不走F,将F当做*
for(int j=1;j<=m;j++)
{
if(mapp[i][j]=='F')ma[i][j]='*';
else ma[i][j]=mapp[i][j];
}
int ans1=bfs(1,1);
for(int i=1;i<=n;i++)//不走M,将M当做*
for(int j=1;j<=m;j++)
{
if(mapp[i][j]=='M')ma[i][j]='*';
else ma[i][j]=mapp[i][j];
}
int ans2=bfs(1,1);
if(min(ans1,ans2)==-1)
{
if(max(ans1,ans2)==-1)cout<<"IMPOSSIBLE"<<endl;
else cout<<max(ans1,ans2)*2<<endl;//要返回,所以乘2
}
else cout<<min(ans1,ans2)*2<<endl;
}
return 0;
}
3.寻找道路-NC16498【NOIP2014提高组】(图论,附加条件bfs)
在有向图G中,每条边的长度均为1,现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
1.路径上的所有点的出边所指向的点都直接或间接与终点连通。
2.在满足条件1的情况下使路径最短。
注意:图G中可能存在重边和自环,题目保证终点没有出边。 请你输出符合条件的路径的长度。
对于30%的数据,0< n≤10,0< m≤20;对于60%的数据,0< n≤100,0< m≤2000;对于100%的数据,0< n≤10,000,0< m≤200,000,0< x,y,s,t≤n,x≠t。
输入描述:
第一行有两个用一个空格隔开的整数n和m,表示图有n个点和m条边。接下来的m行每行2个整数x、y,之间用一个空格隔开,表示有一条边从点x指向点y。最后一行有两个用一个空格隔开的整数s、t,表示起点为s,终点为t。
输出描述:
输出只有一行,包含一个整数,表示满足题目描述的最短路径的长度。如果这样的路径不存在,输出-1。
6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5
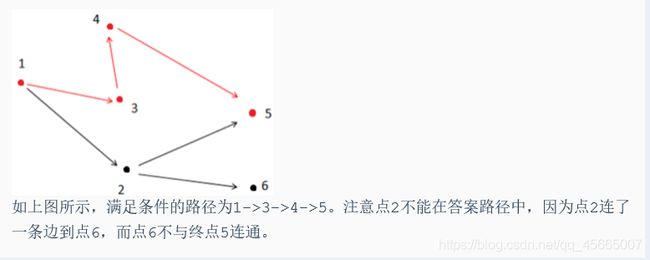
输出:
-1
3
思路:
题目要求找最短路并且路径上的所有点的出边所指向的点都直接或间接与终点连通。建图的时候正向和反向各建一个。
反向用来搜索可以到达终点的点;
正向搜索题目答案;
#include
#define loopx(a,b,i) for(int i=a;i<=b;i++)
#define lson (p<<1)
#define rson ((p<<1)|1)
#define mid ((l+r)>>1)
#define MAX 100005
//char mapp[1005][1005];
//int d[1005][1005];
//int dir[8][2]={1,0,-1,0,0,-1,0,1,1,1,1,-1,-1,1,-1,-1};
int n,m;
int d[10005];//是否走过该节点
int p[10005];//该节点是否可以到达终点
struct node
{
int pot;
int ans;
}now,nex;
vector<int>side[10005];//每个节点的出边指向的点
vector<int>sid[10005];//每个节点的入边源头的点(反向保存原图)
queue<node>que;//solvebfs
queue<int>qu;//findbfs
//int judge(struct node no)
//{
// return no.x>=1&&no.x<=n&&no.y>=1&&no.y<=m&&d[no.x][no.y]==0&&mapp[no.x][no.y]!='*'&&(no.f==0||no.m==0);
//}
void findbfs(int t)//找可以到达终点的点
{
memset(p,0,sizeof(p));
memset(d,0,sizeof(d));
int now,nex;
now=t;
d[t]=1;
p[t]=1;
while(!qu.empty())qu.pop();
qu.push(now);
while(!qu.empty())
{
now=qu.front();
qu.pop();
for(auto i:sid[now])
{
nex=i;
if(d[nex]==1)continue;
d[nex]=1;
p[nex]=1;
qu.push(nex);
}
}
}
int solvebfs(int s,int t)//搜索满足条件的最短路
{
memset(d,0,sizeof(d));
int minn=INF;
int flag;
now.pot=s;
now.ans=0;
d[s]=1;
while(!que.empty())que.pop();
que.push(now);
while(!que.empty())
{
flag=0;
now=que.front();
que.pop();
if(now.pot==t)
{
minn=minn<now.ans?minn:now.ans;
}
for(auto i:side[now.pot])//判断该节点出边节点是否可达终点
if(p[i]==0)flag=1;
if(flag)continue;
for(auto i:side[now.pot])
{
nex.pot=i;
nex.ans=now.ans+1;
if(d[nex.pot]==1)continue;
d[nex.pot]=1;
que.push(nex);
}
}
return minn;
}
int main()
{
cin>>n>>m;
int x,y,s,t;
for(int i=1;i<=m;i++)
{
cin>>x>>y;
side[x].push_back(y);//建图
sid[y].push_back(x);//建反向图
}
cin>>s>>t;
findbfs(t);
if(p[s]==0)cout<<"-1";
else cout<<solvebfs(s,t);
return 0;
}
4.华容道-NC16536【NOIP2013提高组】(bfs+spfa)
小 B最近迷上了华容道,可是他总是要花很长的时间才能完成一次。于是,他想到用编程来完成华容道:给定一种局面, 华容道是否根本就无法完成,如果能完成, 最少需要多少时间。
小B玩的华容道与经典的华容道游戏略有不同,游戏规则是这样的:
1.在一个 n x m 棋盘上有 n x m 个格子,其中有且只有一个格子是空白的,其余 n x m - 1 个格子上每个格子上有一个棋子,每个棋子的大小都是 1 x 1 的;
2.有些棋子是固定的,有些棋子则是可以移动的;
3.任何与空白的格子相邻(有公共的边)的格子上的棋子都可以移动到空白格子上。
游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。
给定一个棋盘,游戏可以玩 q 次,当然,每次棋盘上固定的格子是不会变的, 但是棋盘上空白的格子的初始位置、 指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次玩的时候, 空白的格子在第 EXi 行第 EYi 列,指定的可移动棋子的初始位置为第 SXi 行第 SYi 列,目标位置为第 TXi 行第 TYi 列。
假设小 B每秒钟能进行一次移动棋子的操作,而其他操作的时间都可以忽略不计。请你告诉小 B每一次游戏所需要的最少时间,或者告诉他不可能完成游戏。
对于 30% 的数据, 1 ≤ n, m ≤ 10,q = 1 ;
对于 60% 的数据, 1 ≤ n, m ≤ 30,q ≤ 10 ;
对于 100% 的数据, 1 ≤ n, m ≤ 30,q ≤ 500 。
输入描述:
第一行有 3 个整数,每两个整数之间用一个空格隔开,依次表示 n,m,q ;
接下来的 n 行描述一个 n x m 的棋盘,每行有 m 个整数,每两个整数之间用一个空格隔开,每个整数描述棋盘上一个格子的状态, 0 表示该格子上的棋子是固定的, 1 表示该格子上的棋子可以移动或者该格子是空白的。
接下来的 q 行,每行包含 6 个整数依次是 EXi,EYi,EXi,SYi,TXi,TYi ,每两个整数之间用一个空格隔开,表示每次游戏空白格子的位置,指定棋子的初始位置和目标位置。
输出描述:
共 q 行,每行包含 1 个整数,表示每次游戏所需要的最少时间,如果某次游戏无法完成目标则输出 −1 。
输入:
3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2
输出:
2
-1

思路:
1.首先只有四周有空格时,棋子才能动。可以先bfs预处理每一个可移动棋子四周节点互相在不经过中心节点的情况下,互达的最小路程;
2.再用bfs找到空白格到除开始节点外所有可达节点的最小路;
3.用spfa找符合题目要求的最短路;(暴力bfs会超时)
#include
#define loopx(a,b,i) for(int i=a;i<=b;i++)
#define lson (p<<1)
#define rson ((p<<1)|1)
#define mid ((l+r)>>1)
#define MAX 100005
int mapp[50][50];//图
int dis[50][50];//最短路
int arotime[50][50][5][5];//点x,y的四周在不经过x,y互达的最短路
int sp[50][50][5];//spfa找题目要求最短路,表示点x,y的i方向上有空白格时候的最小路
int record[50][50][5];//spfa标记当x,y的i方向有空白格情况是否在队列中
int dir[8][2]={-1,0,0,1,1,0,0,-1,1,1,1,-1,-1,1,-1,-1};//上右下左,右下,左下,右上,左上
//i=0上,i=1右,i=2下,i=3左
int n,m,q;
int ex,ey,sx,sy,tx,ty;
struct no
{
int x,y;
int pot;
}now,nex;
struct node
{
int x,y;
}noww,nexx;
queue<no>aro;//存储x,y四周可移动的棋子,pot是当前节点相对中心节点的方向
queue<no>sol;//spfa,pot是空白格相对中心节点的方向
queue<node>que;//预处理点x,y的四周在不经过x,y时互达的最短路
//空白格到棋子初始位置最短路
//int judge(struct node no)
//{
// return no.x>=1&&no.x<=n&&no.y>=1&&no.y<=m&&d[no.x][no.y]==0&&mapp[no.x][no.y]!='';
//}
void prebfs(int x,int y)//预处理点x,y的四周在不经过x,y互达的最短路
{
for(int i=0;i<4;i++)//判断四周哪些可移动,放入队列
{
nex.x=x+dir[i][0];
nex.y=y+dir[i][1];
if(nex.x<1||nex.x>n||nex.y<1||nex.y>m||mapp[nex.x][nex.y]==0)continue;
nex.pot=i;
aro.push(nex);
}
while(!aro.empty())//每一次bfs该点到达所有节点的最小路
{
while(!que.empty())que.pop();
memset(dis,inf,sizeof(dis));
noww.x=aro.front().x;
noww.y=aro.front().y;
dis[noww.x][noww.y]=0;
que.push(noww);
int point=aro.front().pot;
aro.pop();
while(!que.empty())
{
noww=que.front();
que.pop();
for(int i=0;i<4;i++)
{
nexx.x=noww.x+dir[i][0];
nexx.y=noww.y+dir[i][1];
if(nexx.x<1||nexx.x>n||nexx.y<1||nexx.y>m)continue;
if(mapp[nexx.x][nexx.y]==0)continue;
if((nexx.x==x&&nexx.y==y)||dis[nexx.x][nexx.y]!=inf)continue;
dis[nexx.x][nexx.y]=dis[noww.x][noww.y]+1;
que.push(nexx);
}
}
for(int i=0;i<4;i++)//存储到达x,y四周的最短路
{
int xx=x+dir[i][0];
int yy=y+dir[i][1];
if(xx<1||xx>n||yy<1||yy>m||mapp[xx][yy]==0)continue;
if(dis[xx][yy]==inf||i==point)continue;
arotime[x][y][point][i]=dis[xx][yy];
//cout<
}
}
}
void whitebfs()//空格到任意位置最短路
{
while(!que.empty())que.pop();
memset(dis,inf,sizeof(dis));
dis[ex][ey]=0;
noww.x=ex;
noww.y=ey;
que.push(noww);
while(!que.empty())
{
noww=que.front();
que.pop();
for(int i=0;i<4;i++)
{
nexx.x=noww.x+dir[i][0];
nexx.y=noww.y+dir[i][1];
if(nexx.x<1||nexx.x>n||nexx.y<1||nexx.y>m)continue;
if(mapp[nexx.x][nexx.y]==0)continue;
if((nexx.x==sx&&nexx.y==sy)||dis[nexx.x][nexx.y]!=inf)continue;
dis[nexx.x][nexx.y]=dis[noww.x][noww.y]+1;
que.push(nexx);
}
}
}
int spfa()
{
if(sx==tx&&sy==ty)return 0;
whitebfs();
// for(int i=1;i<=n;i++)
// {
// for(int j=1;j<=m;j++)
// cout<
// cout<
// }
memset(sp,inf,sizeof(sp));
memset(record,0,sizeof(record));
while(!sol.empty())sol.pop();
for(int i=0;i<4;i++)//让空白格到棋子初始位置四周
{
now.x=sx+dir[i][0];
now.y=sy+dir[i][1];
if(now.x<1||now.x>n||now.y<1||now.y>m)continue;
if(dis[now.x][now.y]==inf||mapp[now.x][now.y]==0)continue;
sp[sx][sy][i]=dis[now.x][now.y];
no re={sx,sy,i};
sol.push(re);
record[sx][sy][i]=1;
}
while(!sol.empty())
{
now=sol.front();
sol.pop();
record[now.x][now.y][now.pot]=0;
//第一种情况:中心点移到空白块
nex.x=now.x+dir[now.pot][0];
nex.y=now.y+dir[now.pot][1];
if(sp[nex.x][nex.y][(now.pot+2)%4]>sp[now.x][now.y][now.pot]+1)
{//移动后现在空白格的位置是上一次的相对位置,左会变成右,上变下
sp[nex.x][nex.y][(now.pot+2)%4]=sp[now.x][now.y][now.pot]+1;
if(record[nex.x][nex.y][(now.pot+2)%4]==0)
{
record[nex.x][nex.y][(now.pot+2)%4]=1;
nex.pot=(now.pot+2)%4;
sol.push(nex);
}
}
//第二种情况:空白块移到中心点四周
for(int i=0;i<4;i++)
{
nex.x=now.x+dir[now.pot][0];
nex.y=now.y+dir[now.pot][1];
if(nex.x<1||nex.x>n||nex.y<1||nex.y>m)continue;
if(mapp[nex.x][nex.y]==0||i==now.pot)continue;
if(arotime[now.x][now.y][now.pot][i]==inf)continue;
int p=sp[now.x][now.y][now.pot]+arotime[now.x][now.y][now.pot][i];
if(sp[now.x][now.y][i]>p)
{
sp[now.x][now.y][i]=p;
if(record[now.x][now.y][i]==0)
{
record[now.x][now.y][i]=1;
no re={now.x,now.y,i};
sol.push(re);
}
}
}
}
int ans=inf;
for(int i=0;i<4;i++)//找最短路
{
ans=min(ans,sp[tx][ty][i]);
}
if(ans==inf)return -1;//不存在
return ans;
}
int main()
{
memset(arotime,inf,sizeof(arotime));
cin>>n>>m>>q;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>mapp[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(mapp[i][j])prebfs(i,j);
while(q--)
{
cin>>ex>>ey>>sx>>sy>>tx>>ty;
cout<<spfa()<<endl;
}
return 0;
}
