快速排序及优化(Java版)
快速排序(Quicksort)是对冒泡排序的一种改进。快速排序由C. A. R. Hoare在1962年提出。

代码实现:
package QuickSort;
public class QuickSortRealize {
public static void QuickSort(int[] arr){
QSort(arr,0,arr.length-1);
}
//对顺序表子序列作快速排序 待排序序列的最小下标值low和最大下标值high
public static void QSort(int[] arr,int low,int high){
int pivot;
if(low//将数组子序列一分为二
QSort(arr, low, pivot-1);//对低子表递归排序
QSort(arr, pivot+1, high);//对高子表递归排序
}
}
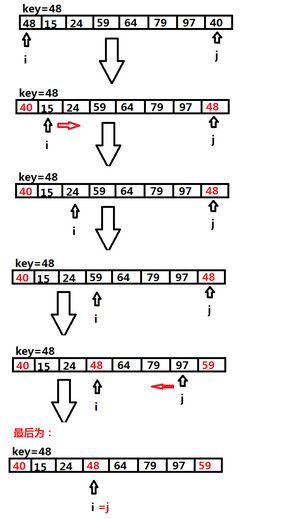
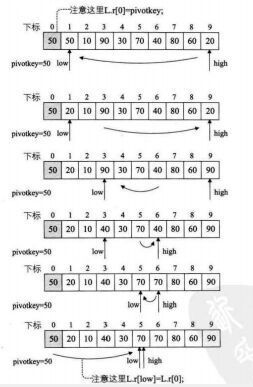
//选择一个关键字,想尽办法将它放到一个位置,使得它左边的值都比它小,
//右边的值都比它大,我们称这个关键字叫枢轴。
public static int Partition(int[] arr,int low,int high){
if(arr == null || low<0 || high>=arr.length){
new Exception();
}
int pivotkey;
pivotkey = arr[low];//选取第一个记录作枢轴记录
while(low//从表的两端向中间扫描
{
while(low=pivotkey){//如果大于枢轴值,则下标减一,否则,跳出循环。
high--;
}
Swap(arr, low, high);//交换
while (low//如果小于枢轴值,则下标加一,否则,跳出循环。
low++;
}
Swap(arr, low, high);//交换
}
return low;
}
public static void Swap(int[] arr,int low,int high){
int temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;
}
public static void main(String[] args) {
int[] arr = {50,10,90,30,70,40,80,60,20};
QuickSort(arr);
for (int array : arr) {
System.out.print(array+" ");
}
System.out.println();
}
} 快速排序的时间性能取决于快速排序递归的深度,可以用递归数来描述算法的执行情况。如果递归树是平衡的,那么此时的性能也是最好的。
也就是说,在最优的情况下,快速排序算法的时间复杂度为 O(nlogn)。
就空间复杂度来说,主要是递归造成的栈空间的使用,最好情况,递归树的深度log2n ,其空间复杂度也就为 O(logn) ,最坏情况,需要进行递归调用,其空间复杂度为 O(n),平均情况 空间复杂度也为 (logn)。
可惜的是 关键字的比较和交换是跳跃进行的,因此,快速排序是 种不稳
定的排序方法。
优化算法:
1、优化选取枢轴
三数取中,即取三个关键字先进行排序,将中间数作为枢轴, 一般是取左端、右端和中间三个数, 也可以随机选取。
对于非常大的待排序的序列来说还是不足以保证能够选择出一个好的pivo tkey, 因此还有个办法是所谓的九数取中,先从数组中分三次取样,每次取三个数,三个样品各取出中数,然后从这三个中数当中再取出一个中数作为枢轴 。
package QuickSort;
public class QuickSortRealize {
public static void QuickSort(int[] arr){
QSort(arr,0,arr.length-1);
}
//对顺序表子序列作快速排序 待排序序列的最小下标值low和最大下标值high
public static void QSort(int[] arr,int low,int high){
int pivot;
if(low//将数组子序列一分为二
QSort(arr, low, pivot-1);//对低子表递归排序
QSort(arr, pivot+1, high);//对高子表递归排序
}
}
//选择一个关键字,想尽办法将它放到一个位置,使得它左边的值都比它小,
//右边的值都比它大,我们称这个关键字叫枢轴。
public static int Partition(int[] arr,int low,int high){
if(arr == null || low<0 || high>=arr.length){
new Exception();
}
int pivotkey;
ChoosePivotkey(arr,low,high);//选取枢轴值
pivotkey = arr[low];
while(low//从表的两端向中间扫描
{
while(low=pivotkey){//如果大于枢轴值,则下标减一,否则,跳出循环。
high--;
}
Swap(arr, low, high);//交换
while (low//如果小于枢轴值,则下标加一,否则,跳出循环。
low++;
}
Swap(arr, low, high);//交换
}
return low;
}
public static void Swap(int[] arr,int low,int high){
int temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;
}
//三数取中 选择枢轴 将枢轴值调至第一个位置
public static void ChoosePivotkey(int[] arr,int low,int high){
int mid = low + (int)(high-low)/2;
if(arr[low]>arr[high]){//保证左端较小
Swap(arr, low, high);
}
if(arr[mid]>arr[high]){//保证中间较小
Swap(arr, mid, high);
}
//此时最大值在最右边
if(arr[mid]>arr[low]){//保证中间较小
Swap(arr, mid, low);
}
}
public static void main(String[] args) {
int[] arr = {50,10,90,30,70,40,80,60,20};
QuickSort(arr);
for (int array : arr) {
System.out.print(array+" ");
}
System.out.println();
}
}
2、优化不必要的交换
package QuickSort;
public class QuickSortRealize3 {
public static void QuickSort(int[] arr){
QSort(arr,0,arr.length-1);
}
//对顺序表子序列作快速排序 待排序序列的最小下标值low和最大下标值high
public static void QSort(int[] arr,int low,int high){
int pivot;
if(low//将数组子序列一分为二
QSort(arr, low, pivot-1);//对低子表递归排序
QSort(arr, pivot+1, high);//对高子表递归排序
}
}
//选择一个关键字,想尽办法将它放到一个位置,使得它左边的值都比它小,
//右边的值都比它大,我们称这个关键字叫枢轴。
public static int Partition(int[] arr,int low,int high){
if(arr == null || low<0 || high>=arr.length){
new Exception();
}
int pivotkey;
pivotkey = arr[low];//选取第一个记录作枢轴记录
int tempCopy = pivotkey;//将枢轴值备份到tempCopy中
while(low//从表的两端向中间扫描
{
while(low=pivotkey){//如果大于枢轴值,则下标减一,否则,跳出循环。
high--;
}
//Swap(arr, low, high);//交换
arr[low] = arr[high];//采用替换而不是交换的方式进行操作
while (low//如果小于枢轴值,则下标加一,否则,跳出循环。
low++;
}
//Swap(arr, low, high);//交换
arr[high] = arr[low];//采用替换而不是交换的方式进行操作
}
arr[low] = tempCopy;//将枢轴值替换回arr[low]
return low;//返回枢轴值所在位置
}
public static void Swap(int[] arr,int low,int high){
int temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;
}
public static void main(String[] args) {
int[] arr = {50,10,90,30,70,40,80,60,20};
QuickSort(arr);
for (int array : arr) {
System.out.print(array+" ");
}
System.out.println();
}
} 3、优化小数组时的排序方案
快速排序适用于非常大的数组的解决办法, 那么相反的情况,如果数组非常小,其实快速排序反而不如直接插入排序来得更好(直接插入是简单排序中性能最好的)。其原因在于快速排序用到了递归操作,在大量数据排序时,这点性能影响相对于它的整体算法优势是可以忽略的,但如果数组只有几个记录需要排序时,这就成了大材小用,因此我们需要改进一下 QSort函数。
package QuickSort;
public class QuickSortRealize4 {
final static int MAX_LENGTH_INSERT_SORT = 7;
public static void QuickSort(int[] arr){
QSort(arr,0,arr.length-1);
}
//对顺序表子序列作快速排序 待排序序列的最小下标值low和最大下标值high
public static void QSort(int[] arr,int low,int high){
int pivot;
if((high-low)>MAX_LENGTH_INSERT_SORT){
pivot = Partition(arr,low,high);//将数组子序列一分为二
QSort(arr, low, pivot-1);//对低子表递归排序
QSort(arr, pivot+1, high);//对高子表递归排序
}
else{
insertSort(arr);
}
}
//选择一个关键字,想尽办法将它放到一个位置,使得它左边的值都比它小,
//右边的值都比它大,我们称这个关键字叫枢轴。
public static int Partition(int[] arr,int low,int high){
if(arr == null || low<0 || high>=arr.length){
new Exception();
}
int pivotkey;
pivotkey = arr[low];//选取第一个记录作枢轴记录
int tempCopy = pivotkey;//将枢轴值备份到tempCopy中
while(low//从表的两端向中间扫描
{
while(low=pivotkey){//如果大于枢轴值,则下标减一,否则,跳出循环。
high--;
}
//Swap(arr, low, high);//交换
arr[low] = arr[high];//采用替换而不是交换的方式进行操作
while (low//如果小于枢轴值,则下标加一,否则,跳出循环。
low++;
}
//Swap(arr, low, high);//交换
arr[high] = arr[low];//采用替换而不是交换的方式进行操作
}
arr[low] = tempCopy;//将枢轴值替换回arr[low]
return low;//返回枢轴值所在位置
}
public static void Swap(int[] arr,int low,int high){
int temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;
}
public static void insertSort(int[] arr){
int i,j;
//4,2,1,7,8
for(i=1;iif(arr[i-1]>arr[i]){
//temp=2
int temp = arr[i];//设置哨兵
//必须要保证数组下标>=0,才for循环
for(j= i-1; j>=0&&arr[j]>temp ;j--){
arr[j+1]=arr[j];//arr[1]=4
}
//j=-1
arr[j+1]=temp;//arr[0]=2
//2 4 1 7 8
}
}
}
public static void main(String[] args) {
int[] arr = {50,10,90,30,70,40,80,60,20};
QuickSort(arr);
//insertSort(arr);
for (int array : arr) {
System.out.print(array+" ");
}
System.out.println();
}
} 我们增加了一个判断, high-low不大于某个常数时(有资料认为7较合适,认为5更合理理,实际应用可适当调整) ,就用直接插入排序,这样就能保证最大化地利用两种排序的优势来完成排序。
4、优化递归操作
我们知道,递归对性能是有一定影响的, QSort 函数在其尾部有两次递归操作。
如果待排序的序列划分极端不平衡,递归深度将趋近与N ,而不是平衡时的 logN,就不仅仅是速度快慢的问题了,栈的大小是很有限的,每次递归调用都会耗费一定的空间 ,函数的参数越多,每次递归耗费的空间也越多。如果能减少递归,将会提高性能。我们对 QSort 实施尾递归优化。
package QuickSort;
public class QuickSortRealize5 {
final static int MAX_LENGTH_INSERT_SORT = 7;
public static void QuickSort(int[] arr){
QSort(arr,0,arr.length-1);
}
//对顺序表子序列作快速排序 待排序序列的最小下标值low和最大下标值high
public static void QSort(int[] arr,int low,int high){
int pivot;
if((high-low)>MAX_LENGTH_INSERT_SORT){
while(low//将数组子序列一分为二
QSort(arr, low, pivot-1);//对低子表递归排序
/////////////////////////////////////////////////////
//QSort(arr, pivot+1, high);//对高子表递归排序
low = pivot + 1;
}
}
else{
insertSort(arr);
}
}
//选择一个关键字,想尽办法将它放到一个位置,使得它左边的值都比它小,
//右边的值都比它大,我们称这个关键字叫枢轴。
public static int Partition(int[] arr,int low,int high){
if(arr == null || low<0 || high>=arr.length){
new Exception();
}
int pivotkey;
pivotkey = arr[low];//选取第一个记录作枢轴记录
int tempCopy = pivotkey;//将枢轴值备份到tempCopy中
while(low//从表的两端向中间扫描
{
while(low=pivotkey){//如果大于枢轴值,则下标减一,否则,跳出循环。
high--;
}
//Swap(arr, low, high);//交换
arr[low] = arr[high];//采用替换而不是交换的方式进行操作
while (low//如果小于枢轴值,则下标加一,否则,跳出循环。
low++;
}
//Swap(arr, low, high);//交换
arr[high] = arr[low];//采用替换而不是交换的方式进行操作
}
arr[low] = tempCopy;//将枢轴值替换回arr[low]
return low;//返回枢轴值所在位置
}
public static void Swap(int[] arr,int low,int high){
int temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;
}
public static void insertSort(int[] arr){
int i,j;
//4,2,1,7,8
for(i=1;iif(arr[i-1]>arr[i]){
//temp=2
int temp = arr[i];//设置哨兵
//必须要保证数组下标>=0,才for循环
for(j= i-1; j>=0&&arr[j]>temp ;j--){
arr[j+1]=arr[j];//arr[1]=4
}
//j=-1
arr[j+1]=temp;//arr[0]=2
//2 4 1 7 8
}
}
}
public static void main(String[] args) {
int[] arr = {50,10,90,30,70,40,80,60,20};
QuickSort(arr);
//insertSort(arr);
for (int array : arr) {
System.out.print(array+" ");
}
System.out.println();
}
} 当我们将 if 改成 while 后,因为第一次递归以后,变量low就没有用处了,所以可以将 pivot+1 赋值给low,再循环后,来一次 Partition
(arr,low,high)时,其效果等同于 “QSort(arr, pivot+1, high);”。结果相同,但因采用迭代而不是递归的方法可以缩减堆栈深度,从而提高了整体性能。