Leetcode刷题——树篇1
文章目录
- 1、树(简单篇1)
- 1.1、 938.二叉搜索树的范围和
- 1.2、617.合并二叉树
- 1.3、 226.翻转二叉树
- 1.4、 700.二叉搜索树中的搜索
- 1.5、 590. N叉树的后序遍历
- 1.6、104. 二叉树的最大深度
- 1.7、 589. N叉树的前序遍历
- 1.8、108. 将有序数组转换为二叉搜索树
- 1.9、 559. N叉树的最大深度
- 1.10、 897. 递增顺序查找树
1、树(简单篇1)
1.1、 938.二叉搜索树的范围和
给定二叉搜索树的根结点 root,返回 L 和 R(含)之间的所有结点的值的和。
二叉搜索树保证具有唯一的值。
示例 1:
输入:root = [10,5,15,3,7,null,18], L = 7, R = 15 输出:32
示例 2:
输入:root = [10,5,15,3,7,13,18,1,null,6], L = 6, R = 10 输出:23
提示:
树中的结点数量最多为 10000 个。 最终的答案保证小于 2^31。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/range-sum-of-bst
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路解析:二叉搜索树,很容易想到中序遍历结果就是升序的数据吧。
要求是返回结点的值的和,并且该值在给定范围[L,R]内,并且二叉搜索树具有唯一值,还有两个例子就不仔细分析了。
首先,把二叉搜索树中序遍历,就得到升序的data数组,然后遍历数组,数值在[L,R]之间的就加到和(sum),最后输出结果,搞定收工。
不难想到递归的二叉树遍历,下面给出简单的框架
//二叉树遍历的框架
void traversal(TreeNode *root){
//递归结束条件
if(root==NULL) return;
//前序遍历写这
traversal(root->left);
//中序遍历写这
traversal(root->right);
//后序遍历写这
}
题解代码(C++):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int rangeSumBST(TreeNode* root, int L, int R) {
int res = 0;
traversal(root,L,R,res);
return res;
}
void traversal(TreeNode* root,int &L,int &R,int &res){
if(root ==NULL) return ;
traversal(root->left,L,R,res);
if(root->val>=L && root->val<= R) res +=root->val;
traversal(root->right,L,R,res);
}
};
题解代码(Java):
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
int res = 0;
public int rangeSumBST(TreeNode root, int L, int R) {
res = 0;//计算开始前,结果清0
traversal(root,L,R);
return res;
}
private void traversal(TreeNode root,int L,int R){
if(root==null) return;
traversal(root.left,L,R);
if(root.val>=L&&root.val<=R) res+=root.val;
traversal(root.right,L,R);
}
}
题解代码(Python):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def __init__(self):
self.res = 0
def rangeSumBST(self, root: TreeNode, L: int, R: int) -> int:
self.res = 0
self.traversal(root,L,R)
return self.res
def traversal(self,root: TreeNode,L:int,R:int):
if root != None:
self.traversal(root.left,L,R)
if root.val>=L and root.val<= R:
self.res += root.val
self.traversal(root.right,L,R)
以上提供了三种编程语言的实现,核心还是二叉树遍历的框架,下面是复杂度分析:
时间复杂度:O(n) 遍历的所有的结点
空间复杂度:O(H) H是树的高度,使用递归需要用到栈
1.2、617.合并二叉树
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL
的节点将直接作为新二叉树的节点。示例 1:
输入: Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出: 合并后的树:
3
/ \
4 5
/ \ \
5 4 7
注意: 合并必须从两个树的根节点开始。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/merge-two-binary-trees
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路解析:这里出现了两棵树,并且要对应位置的结点合并起来,形成一棵新的合并树。(简单理理题目的意思)
如果没有什么想法怎么办,那就从简单的图解方法开始吧!

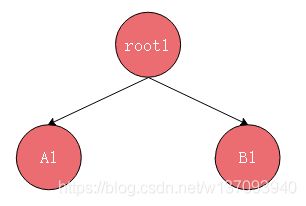
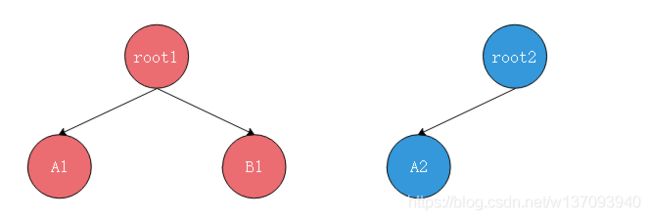
上面是红色和蓝色两棵树,root1是红树的根节点,A1,B1是红树的两棵左右子树(不是一个结点),root2、A2、B2同理。
要把这两棵树合并,是不是先要把root1和root2两个结点合并?
那就root1.val += root2.val ,根节点就搞定了,那返回的合并后的树根节点是合并了,那么左右子树呢?
root1.left = merge(A1,A2) //把A1,A2两棵子树合并了并让其成为root1左子树
root1.right = merge(B1,B2) //把B1,B2两棵子树合并了并让其成为root1右子树
merge()不就是刚刚做的合并工作吗?不就是递归咯!这样的话返回root1,收工!
等等!!!事情真的那么简单吗?递归啊,肯定要有终止条件的吧!
假设仅仅只有一棵红树呢,root2为null,没有蓝树,或者反过来只有蓝树没有红树。例如merge(B1,B2),B2显然是不存在的,那么merge(B1,B2)只需要返回B1即可,所以递归终止条件需要判断子树是否存在。

简单的框架(已经算是实现了):
TreeNode* merge(TreeNode* root1,TreeNode* root2){
//递归终止条件
if(root1==Null) return root2;
if(root2==Null) return root1;
//开始合并
root1->val+=root2->val;
root1->left=merge(root1->left,root2->left);
root1->right=merge(root1->right,root2->right);
return root1;
}
题解代码(C++):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if(t1==NULL) return t2;
if(t2==NULL) return t1;
t1->val+= t2->val;
t1->left = mergeTrees(t1->left,t2->left);
t1->right = mergeTrees(t1->right,t2->right);
return t1;
}
};
题解代码(Java):
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
if(t1==null) return t2;
if(t2==null) return t1;
t1.val+=t2.val;
t1.left=mergeTrees(t1.left,t2.left);
t1.right=mergeTrees(t1.right,t2.right);
return t1;
}
}
题解代码(Python):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
if t1 is None:
return t2
if t2 is None:
return t1
t1.val += t2.val
t1.left = self.mergeTrees(t1.left,t2.left)
t1.right = self.mergeTrees(t1.right,t2.right)
return t1
1.3、 226.翻转二叉树
翻转一棵二叉树。
示例:
输入:
4 / \ 2 7 / \ / \ 1 3 6 9 输出: 4 / \ 7 2 / \ / \ 9 6 3 1来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/invert-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路解析:首先,你要给我一棵树,题目中没有明确说明给的是不是空树,所以要判断,如果是空,那就返回空好了。(养成良好的习惯)
然后,翻转二叉树,看着感觉像是左右子树互换位置一样,大胆假设,小心求证!仔细看看,假设没错!就是那样!(要善于观察例子,例子往往提供很多信息)
简单的框架,递归与交换变量
TreeNode* reversal(TreeNode* root){
if(root==Null) return Null;
//交换左右子树 交换相当熟悉吧
temp = left;
left = right;
right = temp;
reversal(left);//左右子树也要这样操作
reversal(right);//左右子树也要这样操作
return root;
}
题解代码(C++):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root==NULL) return NULL;
TreeNode* temp = root->left;
root->left = root->right;
root->right = temp;
invertTree(root->left);
invertTree(root->right);
return root;
}
};
题解代码(Java):
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root==null) return null;
TreeNode temp = root.left;
root.left=root.right;
root.right = temp;
invertTree(root.left);
invertTree(root.right);
return root;
}
}
题解代码(Python):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if root is None:
return None
root.left,root.right = root.right,root.left #涉及到python的拆包特性,这是python的优点,写起来特舒服,特顺畅
self.invertTree(root.left)
self.invertTree(root.right)
return root
1.4、 700.二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在,则返回
NULL。例如,
给定二叉搜索树:
4 / \ 2 7 / \ 1 3和值: 2 你应该返回如下子树:
2 / \ 1 3
在上述示例中,如果要找的值是 5,但因为没有节点值为 5,我们应该返回 NULL。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/search-in-a-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路解析:
二叉搜索树,出了名了查找快!其实要实现的就是二叉搜索树的查找功能,数据结构最主要的就是遍历、增删查改嘛,现在就是查!
(最无脑的操作:遍历,这样做也可以,但是没有用到二叉搜索树的强大特性了,所以强烈不推荐)

二叉搜索树的特性就是:一个结点的值比它左子树的所有值都大,比它右子树的所有值都小,并且每个结点都符合这种特性。
如上图,假设找3,先和当前结点比较,小于,则进入左子树比较;
再和当前结点比较,大于,则进入右子树比较;
再和当前结点比较,等于,返回该结点。收工!
如果当前结点为空,那就是没找到咯!
简单框架:
TreeNode* search(TreeNode* root,int target){
if(root==NULL) return NULL; //找不到返回空
if(val>target) return search(left);//比当前结点小,搜索左子树
else if(val<target) return search(right);//比当前结点大,搜索右子树
else return root;//找到就返回该结点
}
题解代码(C++):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if(root==NULL) return NULL;
if(root->val>val) return searchBST(root->left,val);
else if(root->val<val) return searchBST(root->right,val);
else return root;
}
};
题解代码(Java):
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if(root==null) return null;
if(root.val>val) return searchBST(root.left,val);
else if(root.val<val) return searchBST(root.right,val);
else return root;
}
}
题解代码(Python):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
if root is None:
return None
if root.val>val:
return self.searchBST(root.left,val)
elif root.val<val:
return self.searchBST(root.right,val)
else:
return root;
1.5、 590. N叉树的后序遍历
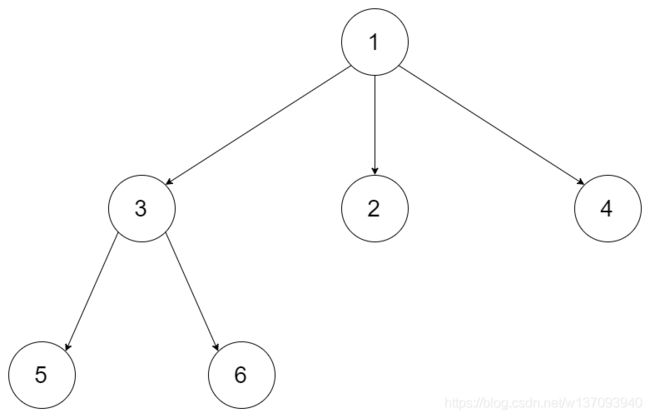
给定一个 N 叉树,返回其节点值的后序遍历。
例如,给定一个 3叉树 :
返回其后序遍历: [5,6,3,2,4,1].
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/merge-two-binary-trees
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路解析:没什么好说的,知道二叉树的遍历自然知道N叉树的遍历,可以加个循环来实现。
简单的框架
//N叉树遍历的框架
void traversal(TreeNode *root){
//递归结束条件
if(root==NULL) return;
//前序遍历写这
for(child:root->childs)
traversal(child);
for(child:root->childs)
traversal(child);
//后序遍历写这
}
(ps:什么?你想问不用递归而是用循环怎么实现遍历?后面再说好吧,慢慢来,不要着急)
题解代码(C++):
/*
// Definition for a Node.
class Node {
public:
int val;
vector children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<int> postorder(Node* root) {
vector<int> res;
postOrderHelper(root,res);
return res;
}
void postOrderHelper(Node* root,vector<int> &res){
if(root==NULL) return;
for(Node* child:root->children)
postOrderHelper(child,res);
res.push_back(root->val);
}
};
题解代码(Java):
/*
// Definition for a Node.
class Node {
public int val;
public List children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
private void postOrderHelper(Node root,List<Integer> res){
if(root==null) return;
for(Node child:root.children)
postOrderHelper(child,res);
res.add(root.val);
}
public List<Integer> postorder(Node root) {
List<Integer> res = new LinkedList<Integer>();
postOrderHelper(root,res);
return res;
}
}
题解代码(Python):
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def postorder(self, root: 'Node') -> List[int]:
res = []
self.postorderHelper(root,res)
return res
def postorderHelper(self,root:'Node',res:List[int]):
if root is not None:
for child in root.children:
self.postorderHelper(child,res)
res.append(root.val)
1.6、104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: 给定二叉树 [3,9,20,null,null,15,7],
3 / \ 9 20 / \ 15 7返回它的最大深度 3 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-depth-of-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路解析:
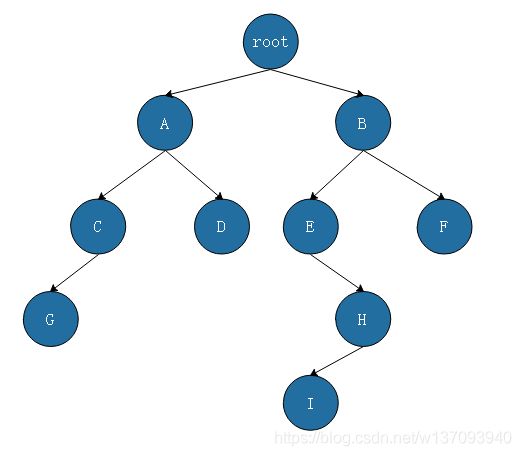
无论一棵多复杂的二叉树,以根结点的树高度总是等于(左子树高度,右子树高度)最大者 + 1,这是很显而易见的。例如root为根节点的二叉树高度=最大值(A为根节点的二叉树高度,B为根节点的二叉树高度)+1 。
那么很容易写出基本框架:
int getHight(TreeNode* root){
int hight = max(leftHight,rightHight)+1;
return hight;
}
那么问题来了,左子树和右子树高度怎么求呢?当然是调用你正在写的这个函数啦,显而易见的递归!
修正基本框架:
int getHight(TreeNode* root){
if(root==NULL) return 0;
int leftHight = getHight(root->left);
int rightHight = getHight(root->right);
int hight = max(leftHight,rightHight)+1;
return hight;
}
递归终止条件如何?
最终没有子树是不是传入NULL?既然是空,那高度就是0,直接返回0。
题解代码(C++):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root ==NULL) return 0;
else
return max(maxDepth(root->left),maxDepth(root->right))+1;
}
};
题解代码(Java):
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if(root==null) return 0;
else
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}
}
题解代码(Python):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if root is None:
return 0
else:
return max(self.maxDepth(root.left),self.maxDepth(root.right))+1
1.7、 589. N叉树的前序遍历
给定一个 N 叉树,返回其节点值的前序遍历。
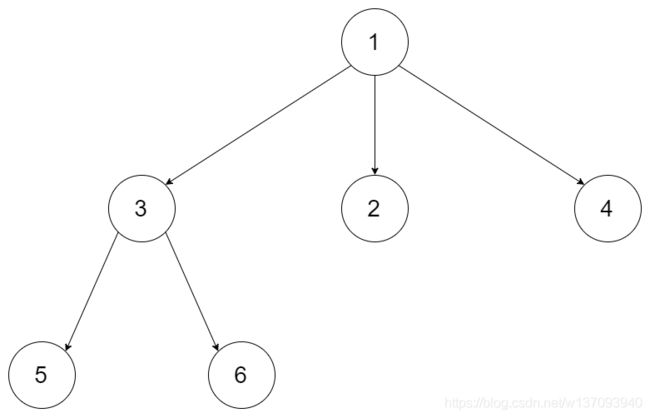
例如,给定一个 3叉树 :
返回其前序遍历: [1,3,5,6,2,4]。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-depth-of-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路解析:其实这个问题已经解决过了,就在1.5小节
这里直接给代码。
框架
//N叉树遍历的框架
void traversal(TreeNode *root){
//递归结束条件
if(root==NULL) return;
//前序遍历写这
for(child:root->childs)
traversal(child);
for(child:root->childs)
traversal(child);
//后序遍历写这
}
题解代码(C++):
/*
// Definition for a Node.
class Node {
public:
int val;
vector children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<int> preorder(Node* root) {
vector<int> res;
preOrderHelper(root,res);
return res;
}
void preOrderHelper(Node* root,vector<int> &res){
if(root==NULL) return;
res.push_back(root->val);
for(Node* child:root->children)
preOrderHelper(child,res);
}
};
题解代码(Java):
/*
// Definition for a Node.
class Node {
public int val;
public List children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
private void preOrderHelper(Node root,List<Integer> res){
if(root==null) return;
res.add(root.val);
for(Node child:root.children)
preOrderHelper(child,res);
}
public List<Integer> preorder(Node root) {
List<Integer> res = new LinkedList<Integer>();
preOrderHelper(root,res);
return res;
}
}
题解代码(Python):
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def preorder(self, root: 'Node') -> List[int]:
res = []
self.preorderHelper(root,res)
return res
def preorderHelper(self,root:'Node',res:List[int]):
if root is not None:
res.append(root.val)
for child in root.children:
self.preorderHelper(child,res)
1.8、108. 将有序数组转换为二叉搜索树
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
给定有序数组: [-10,-3,0,5,9],
一个可能的答案是:[0,-3,9,-10,null,5],它可以表示下面这个高度平衡二叉搜索树:
0 / \ -3 9 / / -10 5来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路解析:
先理清楚什么叫高度平衡二叉树,题目中已经明确说明了,并且从例子中也可以直观理解到平衡二叉树的概念。
下面这种就不叫平衡二叉树了,以-3为根节点的子树,左子树高度为0,右子树高度为0,这就不平衡了.
0 / \ -3 9 / / -10 5 / -99
改成平衡的应该是这样子:
0 / \ -10 9 / \ / -99 -3 5
先是理清楚概念之后,才是真正的解题。
要知道,构造一棵这样的平衡二叉树还是很容易的,如果尽可能保持一个结点的左子树结点数量与右子树结点数量相差为1或相等,那会是什么样的情况?(这句话有点长,多读几遍才容易理解)
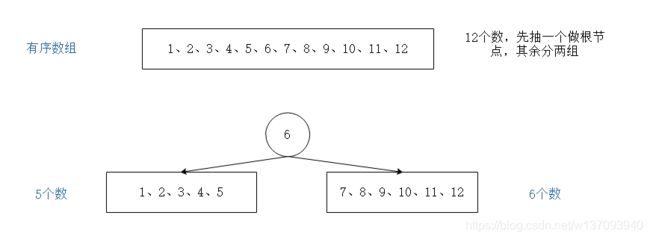
这样一分开,好像有点意思,别着急,我们继续。

分到这里,就更有意思了,平衡平衡,不就是找一个支点,让天平两边相当嘛,当然这里可以允许相差为1。最终得到的平衡二叉树如下图所示:
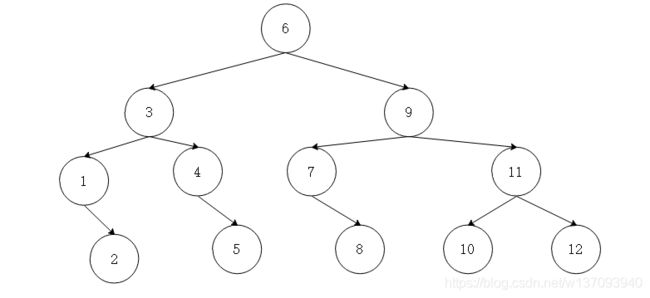
简单描述一下上述过程:
1、找一个支点,保证左右两边数量相差小于等于1;
2、支点作为一个根节点;(支点就是最中间的值嘛)
3、根节点的左孩子是由左分组生成的平衡二叉树;
4、根节点的右孩子是由右分组生成的平衡二叉树.
基本框架:
TreeNode* buildBST(int array[]){
middle = xxx;
root = new TreeNode(middle);
root->left = buildBST(array_left);
root->right = buildBST(array_right);
return root;
}
题解代码(C++):
题解代码(Java):
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
TreeNode root = sortedArrayToBSTHelper(nums,0,nums.length-1);
//java的length、length()、size() 搞得一团糟,不如python一个len()
return root;
}
private TreeNode sortedArrayToBSTHelper(int[] nums,int L,int R){
if(L<=R){
int mid = (int)((L+R)/2);
TreeNode root = new TreeNode(nums[mid]);
root.left=sortedArrayToBSTHelper(nums,L,mid-1);
root.right=sortedArrayToBSTHelper(nums,mid+1,R);
return root;
}else{
return null;
}
}
}
题解代码(Python):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
root = self.sortedArrayToBSTHelper(nums,0,len(nums)-1)
return root
def sortedArrayToBSTHelper(self,nums:List[int],L:int,R:int)->TreeNode:
if L<=R:
mid = (L+R)//2
root = TreeNode(nums[mid])
root.left = self.sortedArrayToBSTHelper(nums,L,mid-1)
root.right = self.sortedArrayToBSTHelper(nums,mid+1,R)
return root
else:
return None
1.9、 559. N叉树的最大深度
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
说明:
树的深度不会超过 1000。 树的节点总不会超过 5000。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路解析:前面已经说了从二叉树遍历到N叉树遍历,现在是从二叉树最大高度到N叉树最大高度,道理都是一样的,做一个推广,直接上代码了!
题解代码(C++):
/*
// Definition for a Node.
class Node {
public:
int val;
vector children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
int maxDepth(Node* root) {
if(root==NULL) return 0;
int max_depth = 0;
for(Node* child:root->children){
int temp = maxDepth(child);
max_depth = max_depth>=temp?max_depth:temp;
}
return max_depth+1;
}
};
题解代码(Java):
/*
// Definition for a Node.
class Node {
public int val;
public List children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public int maxDepth(Node root) {
if(root==null) return 0;
int max =0;
for(Node child:root.children){
int temp = maxDepth(child);
max = max>=temp?max:temp;
}
return max+1;
}
}
题解代码(Python):
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def maxDepth(self, root: 'Node') -> int:
if root is None:
return 0
res = 0
for child in root.children:
temp = self.maxDepth(child)
res = res if res>=temp else temp
return res+1
1.10、 897. 递增顺序查找树
给你一个树,请你 按中序遍历 重新排列树,使树中最左边的结点现在是树的根,并且每个结点没有左子结点,只有一个右子结点。
示例 :
输入:[5,3,6,2,4,null,8,1,null,null,null,7,9]
5 / \ 3 6 / \ \ 2 4 8 / / \ 1 7 9输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
提示:给定树中的结点数介于 1 和 100 之间。 每个结点都有一个从 0 到 1000 范围内的唯一整数值。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/increasing-order-search-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路解析:中序遍历得到结果数组,然后构造一棵新的数,这是很简单的一件事情,这种方法不是就地修改,而是创建新数据。
下面主要介绍的是就地修改方法:
中序遍历还是那个中序遍历,只不过中序遍历的时候,应该进行什么操作呢?最初的方法是直接输出结点的值,而就地修改呢?怎么个就地修改法?
先看图吧:

当中序遍历到第一个输出元素时,也就是1结点,这时候需要把1结点的左孩子置为NULL,而右孩子应该是指向2结点,但是我们没办法有一个指针指向2结点啊,那就遍历到2结点的时候,再把1结点的右孩子修改吧。

发现了没有,pre指针的作用,现在修改1结点的右孩子很容易了吧。
基本框架:
void buildTree(TreeNode* root,TreeNode* pre){
if(root==NULL) return ;
buildTree(root->left);
//中序遍历操作写这
root->left = NULL; //左孩子置空
pre->right = root; //上一个遍历的结点的右孩子指向当前的结点
pre = root; //遍历完当前结点,root相对于下一个结点就是pre了
buildTree(root->right);
}
题解代码(C++):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* increasingBST(TreeNode* root) {
TreeNode *pre=NULL,*head=NULL;//head指针是要指向第一个遍历到的结点
buildTree(root,pre,head);
return head;
}
void buildTree(TreeNode* root,TreeNode*& pre,TreeNode*& head){//C++里面有指针引用,果然指针用起来特别棒
if(root==NULL) return;
buildTree(root->left,pre,head);
root->left=NULL;
if(pre==NULL) head=root;//pre为NULL的时候,遍历到的就是第一个结点
else pre->right = root;
pre = root;
buildTree(root->right,pre,head);
}
};
题解代码(Java):
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
TreeNode pre;
private void buildTree(TreeNode root){
if(root==null) return;
buildTree(root.left);
root.left=null;
pre.right = root;
pre = root;
buildTree(root.right);
}
public TreeNode increasingBST(TreeNode root) {
TreeNode res=new TreeNode(0);//Java没有指针,只能另辟蹊径,多创建一个结点作为头节点
pre = res;
buildTree(root);
return res.right;
}
}
题解代码(Python):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def __init__(self):
self.pre = None
def buildTree(self,root:TreeNode):
if root is not None:
self.buildTree(root.left)
root.left=None
self.pre.right = root
self.pre = root
self.buildTree(root.right)
def increasingBST(self, root: TreeNode) -> TreeNode:
res = TreeNode(0)
self.pre = res
self.buildTree(root)
return res.right