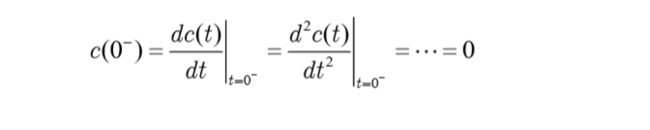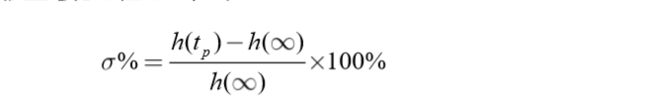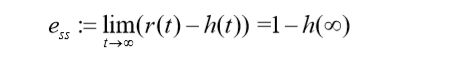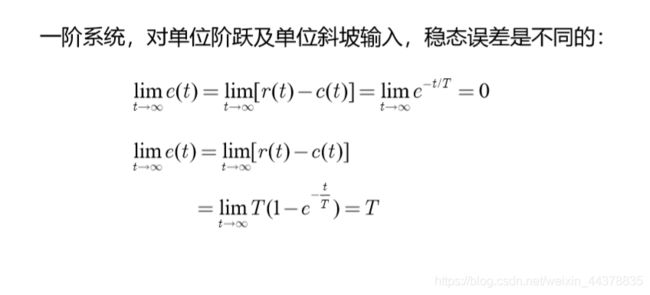(三)【自控原理】（第三章 线性系统的时域分析法）
文章目录
- A 时域分析法基础
- B 一阶系统性能分析与计算
- C 二阶系统分析与计算
- D 系统稳定性分析法（一）
- E 系统稳定性分析法（二）
- F 稳态误差分析计算
A 时域分析法基础
1 时域分析法特点
- 根据系统微分方程，通过拉氏变换直接求出系统的时间响应；
- 依据响应的表达式及时间响应曲线分析系统性能，
找 出系统结构、参数与这些性能之间的关系； - 是一种直接方法，准确且可提供系统时间响应的全部 信息。
2 典型的初始状态、典型外作用
系统的时间响应，不仅取决于系统本身的结构参数，还有系统的初始状态，以及加在系统的外作用相关。
（1）典型初始状态
在t=0–时，系统处于静止状态，即
（2）典型外作用
 |
 |
 |
 |
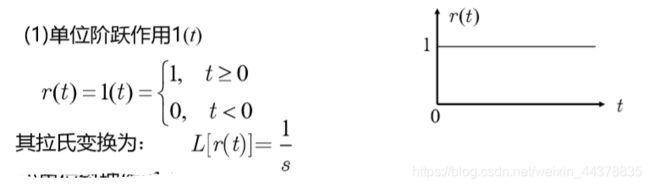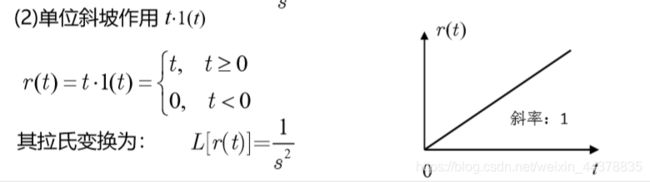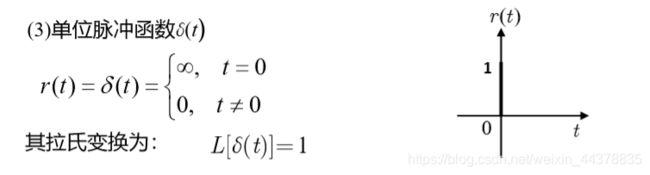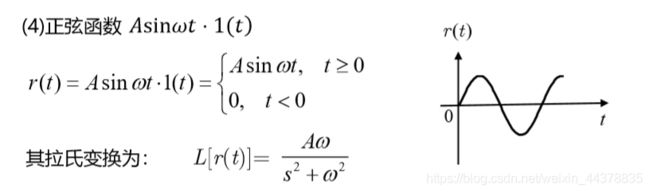3 典型时间响应
初始状态为零的系统，在典型外作用下的输出，称为 典型时间响应。
 |
 |
 |
 |
4 阶跃响应的性能指标
| 延迟时间 t d t_d td | 指单位阶跃响应曲线h(t)上升到其稳态值的50% 所需要的时间。 |
| 上升时间 t T t_T tT | 指单位阶跃响应曲线h(t)，从稳态值的10%上升到 90%所需的时间。有时候也定义为初始值上升到稳态值的时间 |
| 峰值时间 t p | 指单位阶跃响应曲线h(t) 超过其稳态值而达到第 一个峰值所需的时间。 |
| 超调量 σ % \sigma\% σ% | 指单位阶跃响应曲线h(t)，超出稳态值的最大偏 移量与稳态值之比，即： |
| 调节时间 t s t_s ts | ：在单位阶跃响应曲线h(t)的稳态值附近，取 ± 5 % h ( ∞ ) \pm5\%h(\infty) ±5%h(∞)或 ± 2 % h ( ∞ ) \pm2\%h(\infty) ±2%h(∞)作为误差带，响应曲线达到并不在超出该误差带的最小时间。 |
| 稳态误差ess | 指响应的稳态值与期望值之差：  |
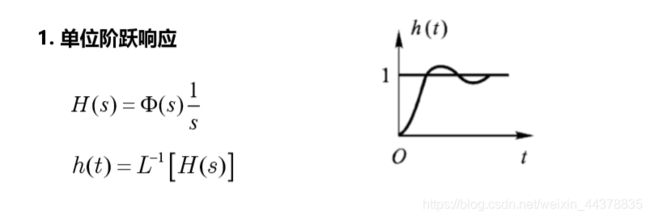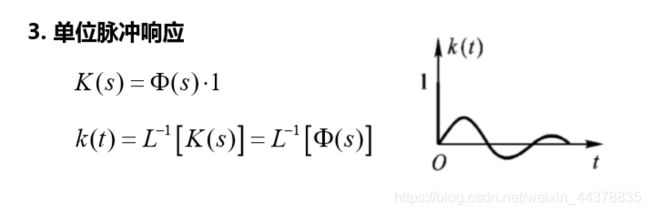B 一阶系统性能分析与计算
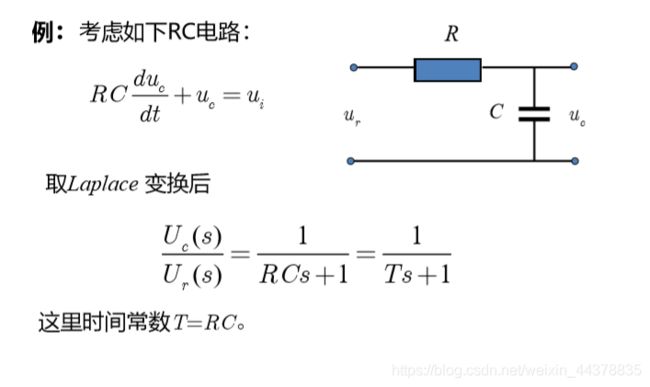
1 数学模型
一阶微分方程描述的系统，称为一阶系统。设系统的微分方程为：
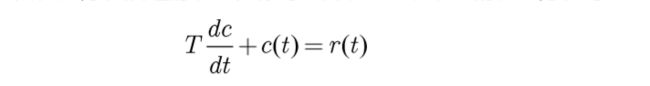
其中，T 为时间常数。许多物理系统均可用一阶系统来描述其动态过程。
2. 单位阶跃响应
 |
 |
 |
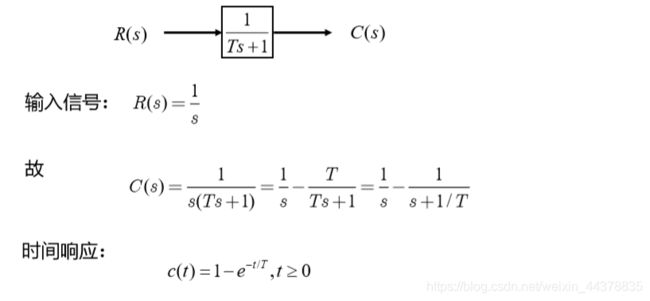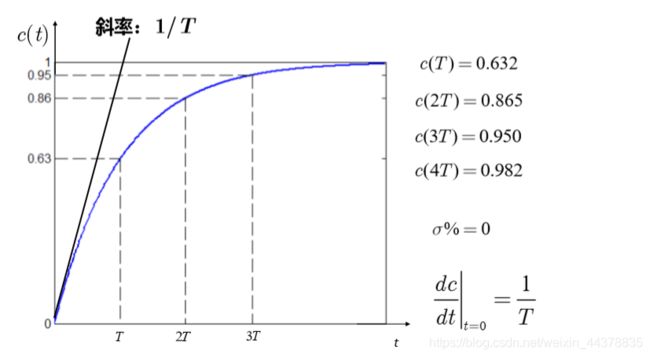3. 单位斜坡响应
 |
 |
总结：
- 一阶系统的阶跃响应是非振荡的、无超调，响应的快速性仅 取决于时间常数T。
- 一阶系统在单位斜坡信号作用下，存在稳态误差。
需要强调的是：系统时域响应的快速性及平稳性仅在阶跃信号作用下才有意义，而稳态误差在其它信号作用下也可以计 算。
C 二阶系统分析与计算
1 数学模型
二阶微分方程描述的系统，称为二阶系统。设系统的微分方程
为：
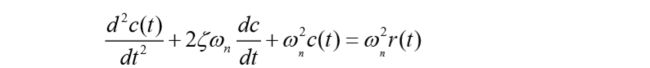
其中 w n w_n wn为无阻尼自然角频率(弧度/秒)， ζ \zeta ζ为阻尼比。
闭环系统传递函数：
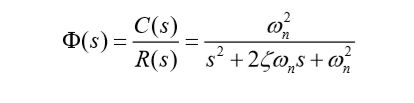
方框图：
解方程求得特征根：
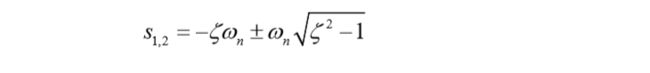
ζ \zeta ζ取值不同，二阶系统的特征根也不同：
 |
 |
 |
 |
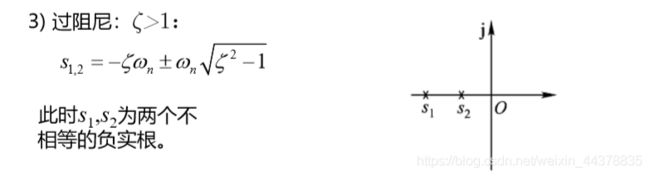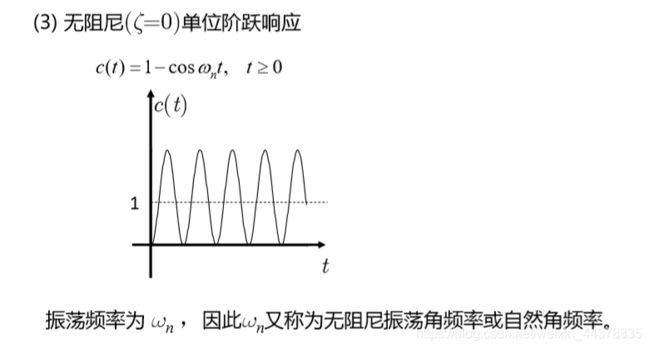
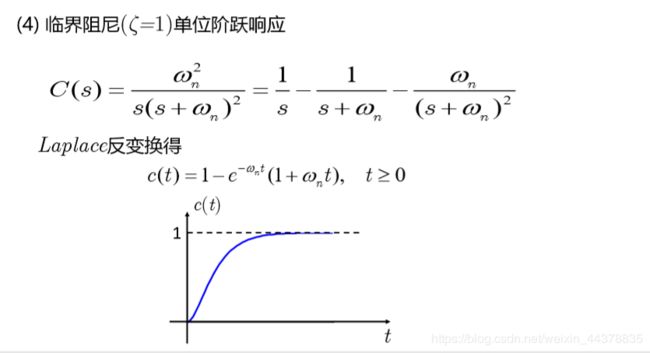
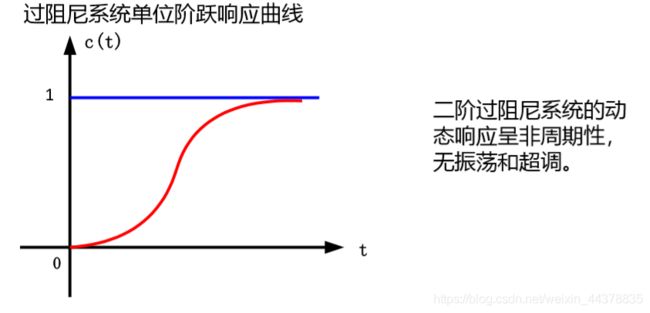
2 二阶系统的单位阶跃响应
 |
 |
 |
 |
 |
 |
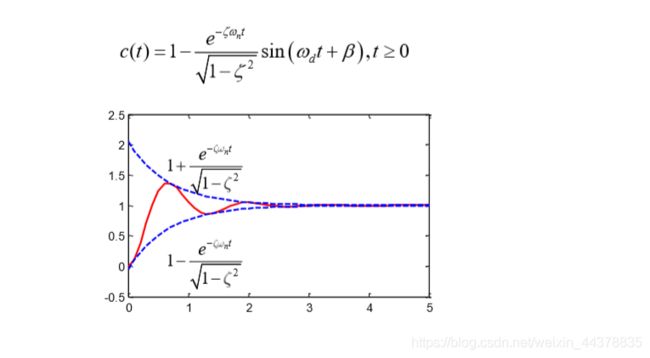3 二阶欠阻尼系统性能的定性分析
 |
 |
 |
 |
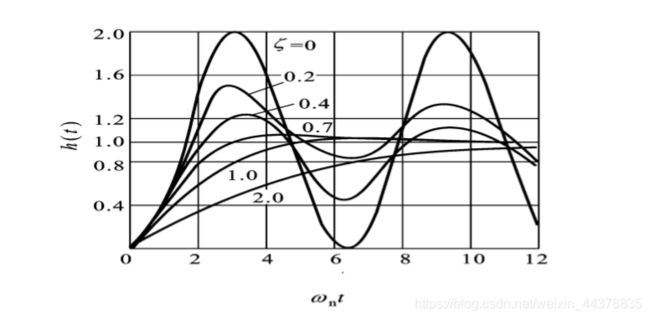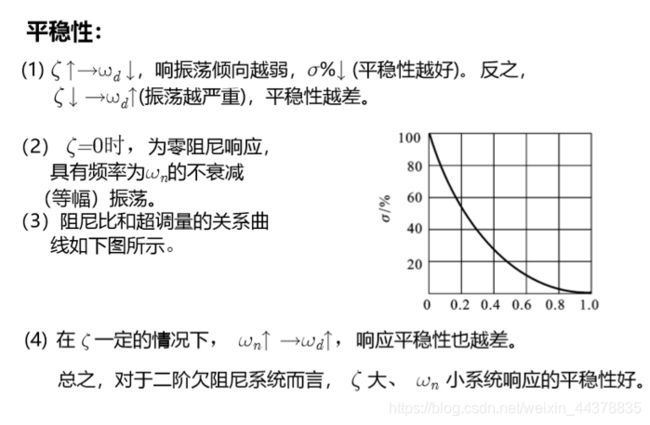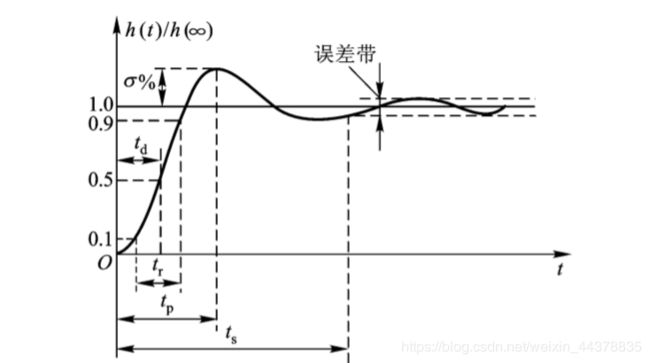
4 欠阻尼系统的性能指标
 |
 |
 |
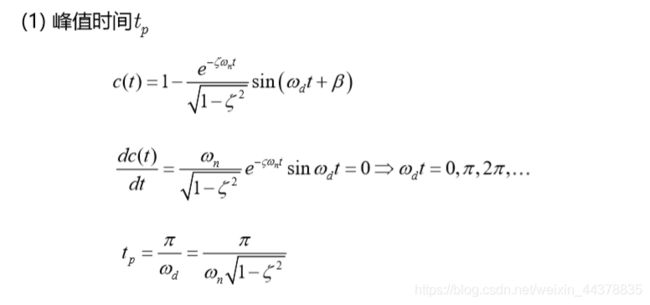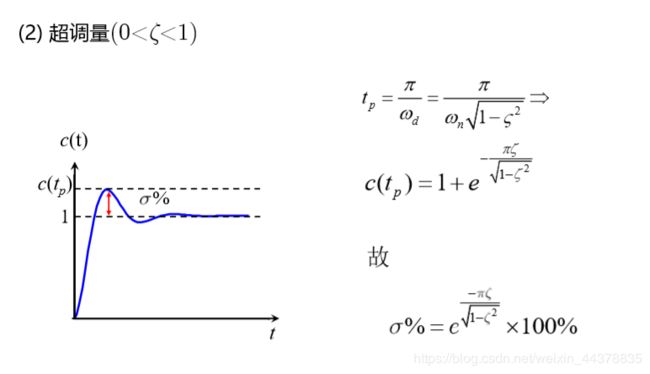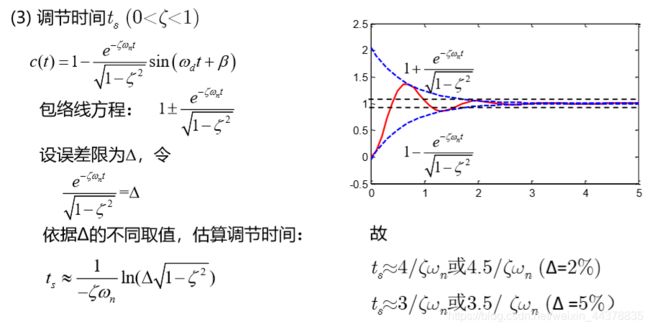5 ζ > 1 \zeta>1 ζ>1 时系统的性能指标
 |
 |
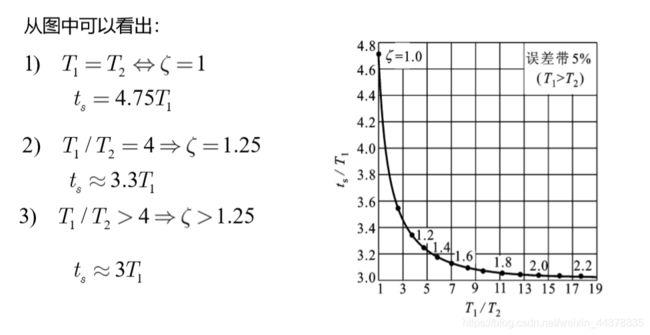D 系统稳定性分析法（一）
**1 稳定性概念 **
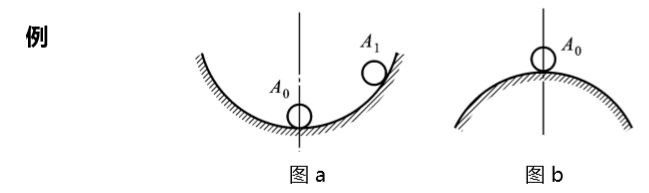
a稳定；b不稳定；
一个控制系统，如果受到扰动，偏离原来的工作状态，当扰动消失后， 若能恢复到原来的工作状态，则称系统是稳定的，否则，系统不稳定。
稳定性可以理解为系统自身的恢复能力，是系统的一种固有特性。对于线性 定常系统，稳定性只取决于系统的结构、参数，与初始条件和外作用无关。
2 稳定的数学条件
 |
 |
 |
 |
ps：欧拉方程
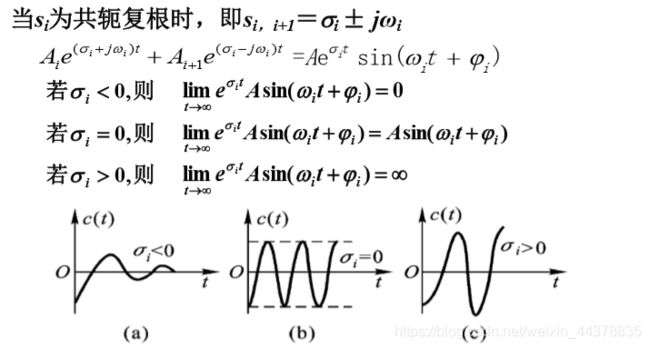系统稳定的充分必要条件是：
系统的特征方程的所有根都具有负实部，或者说都位于s平面的虚轴之左。
如果特征方程有重根，则脉冲响应中具有如下各分量：
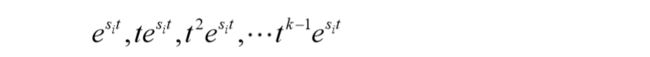
k 为重根个数，当时间t 趋近无穷时，这些分量是否收敛到零，仍取决于 特征根 s i s_i si的性质。
结论:
判断系统是否稳定，可以归结为判断系统特征根实部的符号：
所有特征根均具有负实部，即 R e s i < 0 ( i = 1 , 2 , 3 , . . . , n ) Res_i<0(i=1,2,3,...,n) Resi<0(i=1,2,3,...,n) ，系统是稳定的；
只要有一根特征根的实部大于零，系统不稳定；
若有实部为零的单根， 而其余的特征根都具有负实部，系统处于临界情况，即系统既不发散， 也不能恢复到原来的状态，也属于不稳定情况，如果有实部为零的重根， 系统会发散。
E 系统稳定性分析法（二）
对于高阶方程，计算特征根比较困难，因此使用一种不用计算特征根的方法，直接计算系数即可。
1 劳斯（Routh)稳定性判据
 |
 |
劳斯判据
- 闭环系统稳定当且仅当
(1)D(s) 的所有系数为正；
(2)劳斯表的第一列的所有元素为正。 - D(s) 正实部根的个数等于劳斯表第一列元素符号改变的次数。
劳斯判据的特殊情况
- (1) 第一列某个元素为零，但该行其它元素非零；
- (2) 某行的元素全为零。
情况1：用小正数 ε \varepsilon ε代替第一列的零元素。
 |
 |
情况2：某一行元素全为零(就会出现大小相等方向相反实根或者共轭复根)
 |
 |
特征方程可以得到系统一部分根
2 相对稳定性分析
为了保证系统有一定的稳定裕度，还常常用相对稳定性的概念。通 常用实部最大的特征根距虚轴的距离表示系统的相对稳定性和稳定裕度.
为了检验相对稳定性，可将纵轴左移，如图所示。
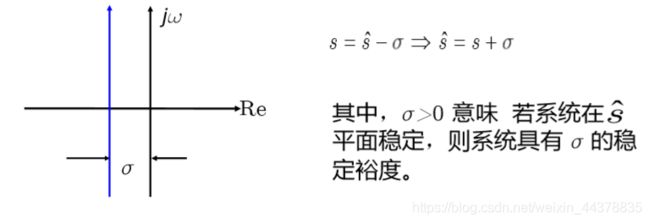
系统稳定条件（1）和（2）
F 稳态误差分析计算
1 误差与稳态误差
（1）误差的两种定义
一种是希望输出与实际输出之差；一种是希望的输出与反馈信号之差。
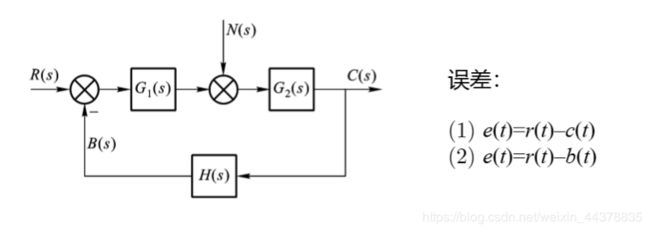
（2） 稳态误差
定义：稳定系统误差的终值称为稳态误差。当时间t时， e(t)极限存在，则稳态误差为
e s s = lim t → ∞ e ( t ) e_{ss}=\lim_{t\rightarrow\infty}e(t) ess=t→∞lime(t)
通常使用终值定理计算：
（3）设 e ( t ) e(t) e(t)的Laplace变换为 E ( s ) E(s) E(s)且 lim s → ∞ e ( t ) \lim_{s\rightarrow\infty}e(t) lims→∞e(t)及 lim s → 0 s E ( s ) \lim_{s\rightarrow 0}sE(s) lims→0sE(s)，则
e s s = lim s → ∞ e ( t ) = lim s → 0 s E ( s ) e_{ss}=\lim_{s\rightarrow\infty}e(t)=\lim_{s\rightarrow 0}sE(s) ess=s→∞lime(t)=s→0limsE(s)
2 稳态误差的计算
一般地， s E ( s ) sE(s) sE(s)是 s s s的有理分式函数，故当且仅当 s E ( s ) sE(s) sE(s)的极点 均具有负实部就可应用下式计算稳态误差：
e s s = lim s → ∞ e ( t ) = lim s → 0 s E ( s ) e_{ss}=\lim_{s\rightarrow\infty}e(t)=\lim_{s\rightarrow 0}sE(s) ess=s→∞lime(t)=s→0limsE(s)
sE(s)的极点均具有负实部的条件中，蕴涵了闭环系统稳定的条件。
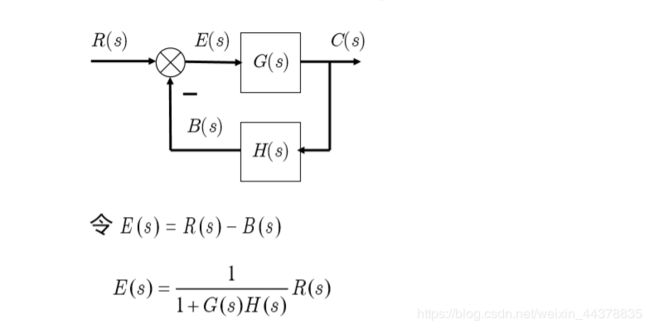
3 输入信号作用下的稳态误差与系统结构参数的关系
 |
 |
 |
N 0 ( s ) 、 D 0 ( s ) N_0(s)、D_0(s) N0(s)、D0(s)均为常数项为1的多项式，所以当s趋近于0时，值为1。
控制系统的稳态误差主要由三方面确定：
- （1)输入信号R(s)
- （2)系统的开环增益K
- （3)系统的型别，即开环传递函数中含有积分环节的个数v。
 |
 |
 |
 |
 |
 |
由以上分析可见，要消除系统在幂函数输入信号作用下的稳态误差， 则要求增加积分环节的数目，要减小系统的稳态误差，则要求提高开 环增益。
总结：
1、系统型别与稳态误差之间的关系仅适用于在输入信号作用下的稳 态误差，不适用于干扰作用下系统的稳态误差，且误差的定义为：
E ( s ) = R ( s ) − B ( s ) E(s)=R(s)-B(s) E(s)=R(s)−B(s)
2、计算稳态误差的步骤可归纳为：
（1）根据误差定义计算E(s）;
（2）判断sE(s)的极点是否均具有负实部；
（3）若sE(s)的极点均具有负实部，应用终值定理计算稳态误差。