动态规划解题模版:区间型
动态规划:区间型
背景:给定一个序列或字符串要进行一些操作,最后一步要将序列或字符串去头、去尾,区间[i,j]变为区间[i+1,j-1],力扣上面的最长回文子串就是这样子操作。区间型dp一般用dp[i] [j],i代表左端点,j代表右端点,若有其他维度可再添加,若两个端点之间存在联系,则可再压缩空间。
区间型dp不开n+1,开n,区间型dp要按照长度去算。不能按照i,要按照j-i。
1、LintCode 667 Longest Palindromic Subsequence
【问题】给一字符串 s,,找出在 s 中的最长回文子序列的长度.。你可以假设 s 的最大长度为 1000。
【分析】注意区分子串和子序列,子串是连续的,子序列可以不连续,这个题是子序列,可以不连续。从最后一步出发,假设S是最长回文子序列,长度为len,分析这个子序列有两种情况
- 子序列长度为1,只有一个字母
- 子序列长度大于1,必有
S[0] = S[len-1]
S是在区间[i,j]中的最长回文子串,对于最长子序列S去头去尾后S[1..len-2]仍然是一个回文串,并且是在区间[i+1,j-1]中的最长回文子串(应该说是在在长度为j-i+1 - 2时的最长回文子串),并且可以得出S[i,j] = S[i+1,j-1] + 2
【转移方程】头尾不想等,去头、去尾各一种情况;头尾相等,同时去头去尾
dp[i][j] = max{dp[i+1][j],dp[i][j-1],dp[i+1][j-1]+2 && chs[i] == chs[j]}
【初始条件】
dp[0][0] = dp[1][1] = ...=dp[n-1][n-1] = 1,每个字母都是长度为1的回文串- 不能按照i去算,要按照长度len去算
【答案】dp[0][n-1] 两个端点,画出图来就是右上三角
public int longestPalindromeSubseq(String s) {
int n = s.length();
char[] chs = s.toCharArray();
if (n <= 1) {
return n;
}
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
dp[i][i] = 1;
}
//region length : 2 <= len <= n
for (int len = 2; len <= n; len++) {
//startIndex i <= n - len
for (int i = 0; i <= n - len; i++) {
int j = i + len - 1;
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
if (chs[i] == chs[j]) {
dp[i][j] = Math.max(dp[i][j], dp[i + 1][j - 1] + 2);
}
}
}
return dp[0][n - 1];
}
要求打印路径
//要求打印出路径
public int LPS(String s) {
char[] chs = s.toCharArray();
int n = chs.length;
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
int[][] dp = new int[n][n];
int[][] path = new int[n][n]; //路径数组
for (int i = 0; i < n; i++) {
dp[i][i] = 1;
}
for (int len = 2; len <= n; len++) {
for (int i = 0; i <= n - len; i++) {
int j = i + len - 1;
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
//去头记为0
if (dp[i][j] == dp[i + 1][j]) {
path[i][j] = 0;
}
//去尾记为1
if (dp[i][j] == dp[i][j - 1]) {
path[i][j] = 1;
}
//相等记为2
if (chs[i] == chs[j]) {
dp[i][j] = Math.max(dp[i][j], dp[i + 1][j - 1] + 2);
if (dp[i][j] == dp[i + 1][j - 1] + 2) {
path[i][j] = 2;
}
}
}
}
//最长的长度为dp[0][n - 1]
char[] res = new char[dp[0][n - 1]];
//开始与结束两个指针
int p = 0, q = dp[0][n - 1];
//chs数组的两个指针
int i = 0, j = n - 1;
//从两头分别往中间去走
while (i <= j) {
//如果字符串长度为1
if (i == j) {
res[p] = chs[i];
break;
}
//如果字符串长度为2
if (i + 1 == j) {
res[p] = chs[i];
res[q] = chs[j];
break;
}
//其他情况,如果来自去头的情况
if (path[i][j] == 0) {
i++;
} else {
if (path[i][j] == 1) { //如果来自去尾的情况
--j;
} else {
res[p++] = chs[i++];
res[q--] = chs[j--];
}
}
}
for (int k = 0; k < res.length; k++) {
System.out.print(res[k]);
}
return dp[0][n - 1];
}
使用记忆化搜索优化,记忆化搜索使用递归,自上而下,递推是自下而上。
int[][] dp = null;
char[] chs = null;
int n;
private void compute(int i, int j) {
//如果算过了就直接返回
if (dp[i][j] != -1) {
return;
}
if (i == j) {
dp[i][j] = 1;
return;
}
//first recursion
compute(i + 1, j);
compute(i, j - 1);
compute(i + 1, j - 1);
//then dp
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
if (chs[i] == chs[j]) {
dp[i][j] = Math.max(dp[i][j], dp[i + 1][j - 1] + 2);
}
}
public int longestPalindromeSubseq(String s) {
chs = s.toCharArray();
n = chs.length;
if (n == 0) {
return 0;
}
dp = new int[n][n];
//初始化所有格子标记为没有被访问过
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
dp[i][j] = -1;
}
}
compute(0, n - 1); //通过递归的方式来填充f数组
return dp[0][n - 1];
}
2、LintCode 200 Longest Palindromic Substring
【问题】给出一个字符串(假设长度最长为1000),求出它的最长回文子串,你可以假定只有一个满足条件的最长回文串。
【分析】一种方法是中心扩展法,另一种以区间型dp来做,假设最长回文字串是s(i,j),那么它的去头去尾的子串s'(i+1..j-1)也是在这个区间内的最长回文子串。假设最长回文子串的长度为len,len的范围是0 <= len <= n,枚举len,只需要记录最长的长度以及起点,就能得到子串。
public static String longestPalindrome2(String s) {
int n = s.length();
char[] chs = s.toCharArray();
boolean[][] dp = new boolean[n][n];
int start = 0;
int longest = 1;
//初始化
for (int i = 0; i < n; i++) {
dp[i][i] = true;
}
//要单独处理下相邻的
for (int i = 0; i < n - 1; i++) {
dp[i][i + 1] = chs[i] == chs[i + 1];
if (dp[i][i + 1]) {
longest = 2;
start = i;
}
}
//长度从3开始
for (int len = 3; len <= n; len++) {
for (int i = 0; i <= n - len; i++) {
int j = i + len - 1;
if (dp[i + 1][j - 1] && chs[i] == chs[j]) {
dp[i][j] = true;
}
if (dp[i][j] && len > longest) {
longest = len;
start = i;
}
}
}
return s.substring(start, start + longest);
}
3、LintCode 396 Coins In A Line III——博弈+区间
【问题】给定一个序列a[0], a[1], …, a[N-1],两个玩家Alice和Bob轮流取数,每个人每次只能取第一个数或最后一个数,双方都用最优策略,使得自己的数字和尽量比对手大,问先手是否必胜。(如果数字和一样,也算是先手胜)
【分析】不需要存己方数字和与对方数字和,只需记录差。两个人都记录着自己与对方的数字之差:SA = A - B,SB = B - A。A取走一个数字m后,B就变为先手,他想要最大化SB = B-A,对于A来说,此时SA = -SB+m,m就是当前这步的数字,m可能是头也可能是尾,选择能最大化SA的即可。取走之后对手也同样采取最优策略去拿。
【转移方程】
-
状态:A先手取头,a[0],B此时最大数字差为SB,此时最大数字差为-SB+a[0]
-
状态:A先手取尾,a[n-1],B此时最大数字差为SB,此时最大数字差为-SB+a[n-1]
-
方程:
dp[i][j] = max{a[i] - dp[i+1][j],a[j] - dp[i][j-1]}
【答案】dp[0][n-1] >= 0则先生胜
public boolean firstWillWin(int[] A) {
int n = A.length;
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
dp[i][i] = A[i];
}
//枚举长度
for (int len = 2; len <= n; len++) {
for (int i = 0; i <= n - len; i++) {
int j = i + len - 1;
dp[i][j] = Math.max(A[i] - dp[i + 1][j], A[j] - dp[i][j - 1]);
}
}
return dp[0][n - 1] >= 0;
}
4、LintCode 430 Scramble String
【问题】攀爬字符串。给定一个字符串S,按照树结构每次二分成左右两个部分,直至单个字符,在树上某些节点交换左右儿子,可以形成新的字符串,判断一个字符串T是否由S经过这样的变换而成。
下面是 s1 = "great" 可能得到的一棵二叉树:
great
/ \
gr eat
/ \ / \
g r e at
/ \
a t
在攀爬字符串的过程中, 我们可以选择其中任意一个非叶节点, 交换该节点的两个子节点.
例如,我们选择了 "gr" 节点,,并将该节点的两个子节点进行交换,并且将祖先节点对应的子串部分也交换,,最终得到了 "rgeat"。 我们认为 "rgeat" 是 "great" 的一个攀爬字符串。
rgeat
/ \
rg eat
/ \ / \
r g e at
/ \
a t
类似地, 如果我们继续将其节点 "eat" 和 "at" 的子节点交换, 又可以得到 "great" 的一个攀爬字符串 "rgtae"。
rgtae
/ \
rg tae
/ \ / \
r g ta e
/ \
t a
给定两个相同长度的字符串 s1 和 s2,判断 s2 是否为 s1 的攀爬字符串。
【分析】给定两个字符串T和S,假设T是由S变换而来
- 如果T和S长度不一样,必定不能变来
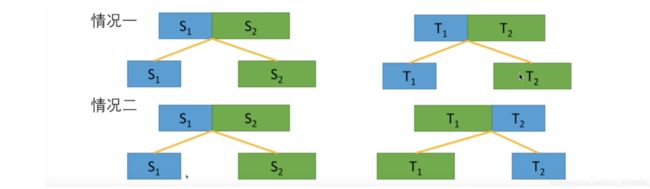
- 如果长度一样,顶层字符串S能够划分为S1和S2,同样字符串T也能够划分为T1和T2
- 情况一:没交换,
S1 ==> T1,S2 ==> T2 - 情况二:交换了,
S1 ==> T2,S2 ==> T1
- 情况一:没交换,
- 子问题就是分别讨论两种情况,T1是否由S1变来,T2是否由S2变来,或 T1是否由S2变来,T2是否由S1变来。
【状态】dp[i][j][k][h]表示T[k…h]是否由S[i…j]变来。由于变换必须长度是一样的,因此这边有个关系j - i = h - k,可以把四维数组降成三维。dp[i][j][len] 表示从字符串S中i开始长度为len的字符串是否能变换为从字符串T中j开始长度为len的字符串
dp[i] [j] [k] = OR1<=w<=k-1{dp[i] [j] [w] AND dp[i+w] [j+w] [k-w]} 或 OR1<=w<=k-1{dp[i] [j+k-w] [w] AND dp[i+w] [j] [k-w]}
枚举S1长度w(1~k-1,因为要划分),f[i] [j] [w]表示S1能变成T1,f[i+w] [j+w] [k-w]表示S2能变成T2,或者是S1能变成T2,S2能变成T1。
【初始条件】对于长度是1的子串,只有相等才能变过去,相等为true,不相等为false。
【答案】dp[0][0][n]
public boolean isScramble(String s1, String s2) {
char[] chs1 = s1.toCharArray();
char[] chs2 = s2.toCharArray();
int n = s1.length();
int m = s2.length();
if (n != m) {
return false;
}
boolean[][][] dp = new boolean[n][n][n + 1];
//初始化单个字符的情况
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j][1] = chs1[i] == chs2[j];
}
}
//枚举长度2~n
for (int len = 2; len <= n; len++) {
//枚举S中的起点位置
for (int i = 0; i <= n - len; i++) {
//枚举T中的起点位置
for (int j = 0; j <= n - len; j++) {
//枚举划分位置
for (int k = 1; k <= len - 1; k++) {
//第一种情况:S1->T1,S2->T2
if (dp[i][j][k] && dp[i + k][j + k][len - k]) {
dp[i][j][len] = true;
break;
}
//第二种情况:S1->T2,S2->T1
if (dp[i][j + len - k][k] && dp[i + k][j][len - k]) {
dp[i][j][len] = true;
break;
}
}
}
}
}
return dp[0][0][n];
}`
5、LintCode 168 Burst Balloons
【问题】有n个气球,编号为0到n-1,每个气球都有一个分数,存在nums数组中。每次吹气球i可以得到的分数为 nums[left] * nums[i] * nums[right],left和right分别表示i气球相邻的两个气球。当i气球被吹爆后,其左右两气球即为相邻。要求吹爆所有气球,得到最多的分数。(最后一个气球被扎破即它本身,算作1 * nums[i] * 1)
【分析】区间型dp,从最后一步出发,最后一步必定扎破一个气球,编号为i,这一步获得金币1* nums[i] * 1,此时i前面的气球1~i-1以及i后面的气球i+1~n都被扎破了,需要知道两边最多能获得多少个金币,再加上最后一步,就是结果。
【状态转移方程】由于最后一步是1 * nums[i] * 1,我们可以认为两端有两个不能扎破的气球,值为1,dp[i] [j]代表扎破i+1号气球~j-1号气球能获得的金币数,i和j是不能被扎破的,因为是两端,并且当前气球k不能被扎破,要分别考虑k的左侧(i~k-1)和右侧(k+1~j),状态转移方程为:
dp[i][j] = max{dp[i][k] + dp[k][j] + a[i] * a[k] * a[j]},k∈(i,j)- dp[i] [k]代表扎破i+1~k-1号气球,dp[k] [j]代表扎破k+1~j-1号气球,再加上扎破这个气球获得的金币数
【初始条件】没有气球要扎破就获得0个金币
dp[0][1] = dp[1][2] = ... = dp[n-2][n-1] = 0
public static int maxCoins(int[] nums) {
int n = nums.length;
int[] A = new int[n + 2]; //左右两个不能扎破的
A[0] = A[n + 1] = 1;
for (int i = 0; i < n; i++) {
A[i + 1] = nums[i];
}
n += 2;
int[][] dp = new int[n][n];
//初始化没有气球要扎破的情况
for (int i = 0; i < n - 1; i++) {
dp[i][i + 1] = 0;
}
//从长度为3开始
for (int len = 3; len <= n; len++) {
//开头
for (int i = 0; i <= n - len; i++) {
//结尾
int j = i + len - 1;
dp[i][j] = Integer.MIN_VALUE;
//枚举中间的气球 作为不扎破的气球
for (int k = i + 1; k <= j - 1; k++) {
dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k][j] + A[i] * A[k] * A[j]);
}
}
}
return dp[0][n-1];
}