【数论/图论】树的计数,prufer(Prüfer)编码,Cayley公式及相应例题
目录
- 1、 p r u f e r prufer prufer编码
- 1)无根树转化为prufer序列
- 2)prufer序列转化为无根树。
- 2、Cayley公式
- 1)由Cayley公式得到四个推论
- 例题1、P4981 父子
- 例二、P4430 小猴打架
部分来自: 大佬的博客,加入了一些自己的理解。
1、 p r u f e r prufer prufer编码
首先引入 p r u f e r prufer prufer编码(其实是 P r u ¨ f e r Prüfer Pru¨fer)
p r u f e r prufer prufer数列,可以用来解一些关于无根树计数的问题。
p r u f e r prufer prufer数列是一种无根树的编码表示,对于一 棵 n n n 个节点带编号的无根树,对应唯一一串长度为n-1的 p r u f e r prufer prufer编码。
1)无根树转化为prufer序列
一棵无根树的 p r u f e r prufer prufer编码的值运算如下:
首先定义无根树中度数为1的节点是叶子节点。 找到编号最小的叶子并删除,序列中添加与之相连的节点编号,重复执行直到只剩下2个节点。
如图:
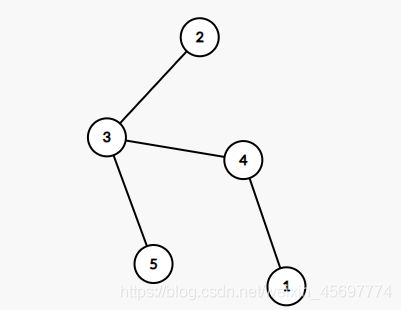
它的 p r u f e r prufer prufer编码就是4, 3, 3
先丢1,4加入序列,再丢2,3加入序列,再丢5,3加入序列,剩余两个,停止丢人,序列为4,3,3
显然,一棵有n个结点的无根树,它的 p r u f e r prufer prufer 编码是唯一的,且有 n − 2 n-2 n−2 个可能相同的元素。
具体实现可以用一个 s e t set set搞定,维护度数为 1 1 1 的节点。复杂度 O ( n l o g n ) O(nlogn) O(nlogn)。
2)prufer序列转化为无根树。
设点集 V = ( 1 , 2 , 3 , . . . , n ) V=(1,2,3,...,n) V=(1,2,3,...,n),每次取出prufer序列中最前面的元素u,在V中找到编号最小的没有在 p r u f e r prufer prufer序列中出现的元素v,给u,v连边然后分别删除,最后在V中剩下两个节点,给它们连边。最终得到的就是无根树。
具体实现也可以用一个 s e t set set,维护 p r u f e r prufer prufer序列中没有出现的编号。复杂度 O ( n l o g n ) O(nlogn) O(nlogn)。
很显然,每一个prufer序列与一棵无根树一一对应。
因此,对于一棵已知有n个结点的无根树,一定有一个n-2长度的序列,那么,我们枚举所有长度为n-2的序列,发现其与所有可能形态的无根树一一对应。而这种序列,根据乘法原理,有**n n-2**个可能的序列。
因此,对于一个已知的n,有n n-2 种不同的无根树。
最后有一个很重要的性质就是 p r u f e r prufer prufer 序列中某个编号出现的次数就等于这个编号的节点在无根树中的度数-1。
(例如最上面的图中4,3,3,4的度数为2,3的度数为3。)
2、Cayley公式
Cayley公式是说,一个无向完全图有 n n − 2 n^{n-2} nn−2 棵生成树,通俗的说就是n个节点的带编号的无根树有 n n − 2 n^{n-2} nn−2个。
刚才Prufer有一个很重要的性质:序列与树是一一对应的
而Prufer序列有n-2项,序列中的每个数都在1到n的范围内。
所以我们可以直接推出n个点的无向完全图的生成树的计数: n n − 2 n^{n-2} nn−2
一个有趣的推广是,n个节点的度依次为D1, D2, …, Dn的无根树共有 ( n − 2 ) ! / [ ( D 1 − 1 ) ! ( D 2 − 1 ) ! . . ( D n − 1 ) ! ] (n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ] (n−2)!/[(D1−1)!(D2−1)!..(Dn−1)!] 个,因为此时 P r u ¨ f e r Prüfer Pru¨fer编码中的数字i恰好出现 D i − 1 Di-1 Di−1次(上面的结论)。
1)由Cayley公式得到四个推论
一棵n个节点的无根树唯一地对应了一个长度为n-2的数列,数列中的每个数都在1到n的范围内。
上面这句话比较重要。通过上面的定理,
1) 我们可以直接推出n个点的无向完全图的生成树的计数:n(n-2) 即n个点的有标号无根树的计数。
2) 一个有趣的推广是,n个节点的度依次为 D 1 , D 2 , … , D n D1, D2, …, Dn D1,D2,…,Dn的无根树共有 ( n − 2 ) ! / [ ( D 1 − 1 ) ! ( D 2 − 1 ) ! . . ( D n − 1 ) ! ] (n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ] (n−2)!/[(D1−1)!(D2−1)!..(Dn−1)!] 个,因为此时 P r u ¨ f e r Prüfer Pru¨fer编码中的数字i恰好出现Di-1次。
即 n种元素,共 n − 2 n-2 n−2个,其中第 i i i 种元素有 D i − 1 Di-1 Di−1个,求排列数。
3) n个节点的度依次为 D 1 , D 2 , … , D n D1, D2, …, Dn D1,D2,…,Dn,令有m个节点度数未知,求有多少种生成树?(BZOJ1005 明明的烦恼)
令每个已知度数的节点的度数为di,有n个节点,m个节点未知度数, l e f t = ( n − 2 ) − ( d 1 − 1 ) − ( d 2 − 1 ) − . . . − ( d k − 1 ) left=(n-2)-(d1-1)-(d2-1)-...-(dk-1) left=(n−2)−(d1−1)−(d2−1)−...−(dk−1)
已知度数的节点可能的组合方式如下
( n − 2 ) ! / ( d 1 − 1 ) ! / ( d 2 − 1 ) ! / . . . / ( d k − 1 ) ! / l e f t ! (n-2)!/(d1-1)!/(d2-1)!/.../(dk-1)!/left! (n−2)!/(d1−1)!/(d2−1)!/.../(dk−1)!/left!
剩余left个位置由未知度数的节点随意填补,方案数为mleft
于是最后有
a n s = ( n − 2 ) ! / ( d 1 − 1 ) ! / ( d 2 − 1 ) ! / . . . / ( d k − 1 ) ! / l e f t ! ∗ m l e f t ans=(n-2)!/(d1-1)!/(d2-1)!/.../(dk-1)!/left! * m^left ans=(n−2)!/(d1−1)!/(d2−1)!/.../(dk−1)!/left!∗mleft
例题1、P4981 父子
#include例二、P4430 小猴打架
P4430 小猴打架
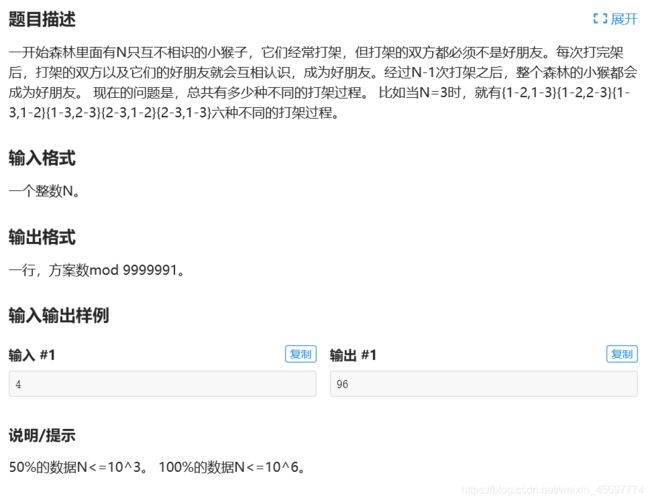
由 C a y l e y Cayley Cayley定理,n个节点的带标号的形态不同的无根树有 n n − 2 n^{n-2} nn−2n 个,这个 p u r f e r purfer purfer序对应的树有 ( n − 1 ) (n-1) (n−1)条边, 如果还要考虑这棵树的生成顺序的话, 那就是 n − 1 n-1 n−1条边全排列: ( n − 1 ) ! (n-1)! (n−1)!
答案 ( n − 1 ) ! ∗ n n − 2 m o d 9999991 (n-1)!*n^{n-2} mod 9999991 (n−1)!∗nn−2mod9999991
#include注:如果您通过本文,有(qi)用(guai)的知识增加了,请您点个赞再离开,如果不嫌弃的话,点个关注再走吧 ! 当然,也欢迎在讨论区指出此文的不足处,作者会及时对文章加以修正 !

