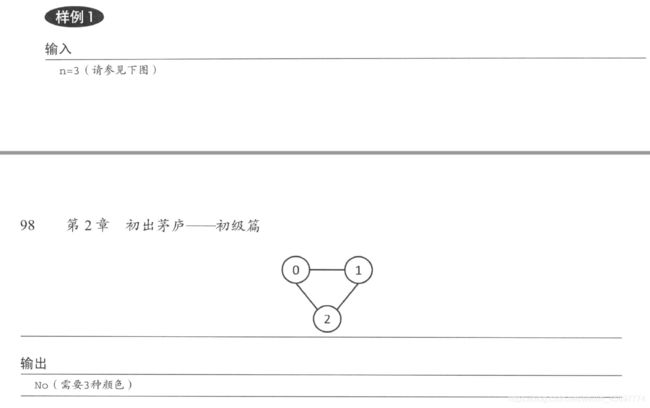
【图论】图，实现图（三种方式），二分图 详解

一.图的基本概念

图（graph）并不是指图形图像（image）或地图（map）。通常来说，我们会把图视为一种由“顶点”组成的抽象网络，网络中的各顶点可以通过“边”实现彼此的连接，表示两顶点有关联。注意上面图定义中的两个关键字，由此得到我们最基础最基本的2个概念，顶点（vertex）和边（edge）。

如上图所示，节点（vertex）用红色标出，通过黑色的边（edge）连接。

1.度

与结点关联的边数，在有向图中为入度与出度之和。

• 出度：在有向图中以这个结点为起点的有向边的数目。(可形象的理解为离开这个结点的边的数目)

• 入度：在有向图中以这个结点为终点的有向边的数目。(可形象的理解为进入/指向这个结点的边的数目)

任意一个图的总度数等于其边数的2倍

2.连通

如果在同一无向图中两个结点存在一条路径相连，则称这两个结点连通。

(1)连通图

如果无向图中任意两个结点都是连通的，则称之为连通图。

(2)强连通/强连通图

如果有向图中任意两个结点之间存在两条路径(即(i,j)两点中，既从i到j有一条路径，j到i也有一条路径)，则两点是强连通的。当一个图中任意两点间都是强连通的，则该图称之为强连通图。

在强连通图中，必定有一条回路经过所有顶点。

强连通分量：非强连通图有向图中的最大子强连通图。

3.回路

起点与相同的路径，又叫“环”。

4.完全图

任意两点间都存在边使其相连的无向图或任意两点间都存在两条不同边的有向图称作完全图

N个顶点的完全图:

有向 有n(n-1)条边
无向 有n(n-1)/2条边

上述内容参考

二. 邻接矩阵实现图

邻接矩阵使用二维数组或vector来表示图，g[i][j]表示顶点i和顶点j的关系
无向图：

• 需要使g[i][j]=g[j][i]

• g[i][j]表示顶点i和顶点j的边数（0/1/2...）（对于重边或自环）

有向图：

• 不需要g[i][j]=g[j][i]

• 一般有权有向图，权值可能为0，所以如果两点之间无边就使g[i][j]=INF

• 若有重边可以根据题意只保存权值最大或最小的边即可

邻接矩阵实现图的优点：

• 可以$O(1)$查询两点之间是否有边

缺点：

• 内存占用过大，$O(V^2)$的空间，对于树这种图而言太过于浪费

#include
using namespace std;
#define debug(x) cout<<"#  "<
typedef long long ll;
const ll mod=2147483647;
const ll N=1e4+7;
struct vertex
{
    vector<vertex*>edge;
    /*
    ******顶点的属性
    */
};
vertex G[N];
int main()
{
    ll V,E;
    scanf("%lld %lld",&V,&E);
    for(int i=0;i<E;++i)
    {
        ll s,t;
        scanf("%lld %lld",&s,&t);
        G[s].edge.push_back(&G[t]);
        //有向图不需要，无向图需要
        //G[t].edge.push_back(&G[s]);
    }
    /*
    *****各种图的操作
    */
    return 0;
}

———————————————————————————————————

vertex* ShortestPath(vertex G[],int query_id,int d)

在这个函数里，作为返回值的G0一切正常，可是在调用ShortestPath函数将其值存入vertex *G0中后，G0中的值全部丢失了。
不要返回局部对象的引用或指针，因为函数完成后，它所占的存储空间也随之释放掉。 因此，函数终止意味着局部变量的引用将指向不再有效的内存区域。此bug来源
———————————————————————————————————

三.邻接表实现图

优点：

• 内存占用较小只需要$O(|V|+|E|)$的内存

缺点：

• 实现带权图较为复杂
• 查询两点是否有边需要遍历一遍链表，每次都是$O(V)$的时间

输入：

3 3 
0 1//有一条0到1的边
0 2
1 2

#include
using namespace std;
#define debug(x) cout<<"#  "<
typedef long long ll;
const ll mod=2147483647;
const ll N=1e4+7;
vector<ll>G[N];//graph
/*
如果边上有属性（带权图）
struct edge
{
    ll to,cost;
};
vectorG[N];
*/
int main()
{
    ll V,E;//V个顶点和E条边
    scanf("%lld %lld",&V,&E);
    for(int i=0;i<E;++i)
    {
        ll s,t;//从s到t
        scanf("%lld %lld",&s,&t);
        G[s].push_back(t);
    }
    /*
    
    **********各种对图的操作
    
    */
    return 0;
}

四.链式前向星实现图

【链式前向星+存图】讲解
链式前向星：
若果有五个点，假设把他们想做是一个个的小房间，每个房间中藏有其他房间的钥匙，每个房间可以通往其他人的房间。现在我来讲一讲他的具体步骤吧：
有一个东西叫做st的里面存储的是第i条路的路径数。 所以呢，我们可以定一个结构体，具体代码如下：

struct node
{
    ll v,nex,val,u;
}e[N];

ll head[N],cnt;

inline void add(ll u,ll v,ll val)//从u到v，从父节点到子节点
{
    e[++cnt].nex=head[u];
    e[cnt].val=val;//可有可无
    e[cnt].v=v;
    e[cnt].u=u;//可有可无
    head[u]=cnt;
}

注意遍历时候的循环跟普通的方法不一样！

for(ll i=head[u];i;i=e[i].nex)
    {
        ll v=e[i].v;
        ---------------
    }

//这样我们就可以遍历全部的点了！！！：）

建议直接把上面的几行代码背下来，具体到底是什么意思懂不懂无所谓，会用就行。

五. 二分图

概述

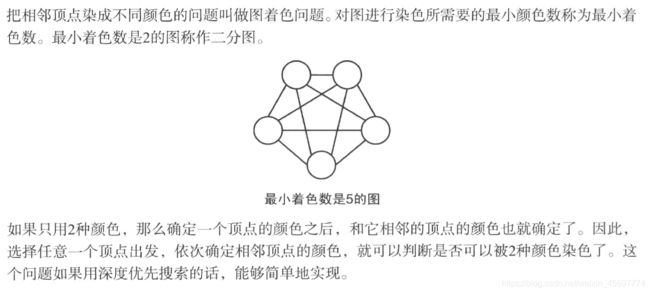
二分图又称作二部图，是图论中的一种特殊模型。设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

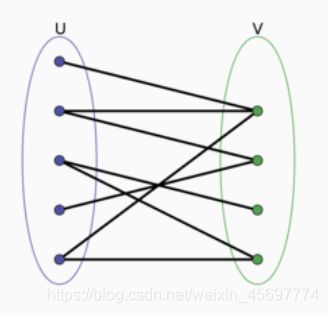
如上图就是一个标准的二分图

1.简单应用—二分图的判定

此题来源于《挑战程序设计竞赛》

DFS

vector<int> G[MAX_V];//图的表示
int V;//顶点数
int color[MAX_V];//顶点i的颜色1或-1
//把顶点染成1或-1
bool dfs(int v,int c)
{
	color[v]=c;//顶点v染成c
	for (int i = 0; i < G[v].size(); ++i)
	{
		//相邻点同色，返回false
		if(color[G[v][i]]==c)
			return false;
		//相邻点没有染色，就将其染色为-c，继续dfs，若最终仍为false，则返回false
		if(color[G[v][i]]==0 && !dfs(G[v][i],-c))
			return false;
	}

	//所有顶点染过色返回true
	return true;
}
void solve()
{
	//如果是连通图，则一次dfs即可访问所有位置
	//但题目没有说明，故要依次检查各个顶点的情况
	for (int i = 0; i < V; ++i)
	{
		if (color[i]==0)
		{
			//如果顶点还没有染色，染成1
			if (!dfs(i,1))
			{
				cout<<"No"<<endl;
				return;
			}
		}
	}
	cout<<"Yes"<<endl;
}

以及BFS

int n,m;
vector<int> g[MAXN];
int color[MAXN];
void init()
{
	for(int i=0;i<n;i++){
		g[i].clear();
		color[i]=-1;
	}
}
int bfs()
{
	queue<int>q;
	q.push(0);
	color[0]=1;
	while(!q.empty()){
		int t = q.front();
		q.pop();
		for(int i=0;i<g[t].size();i++){
			if(color[g[t][i]]==color[t])//相邻节点颜色相同，不是二分图
			return 1;
			else if(color[g[t][i]]==-1)//未染色
			{
				color[g[t][i]]=-color[t];
				q.push(g[t][i]);
			}
		}
	}
	return 0;
}

#include
#define MAX_V 210
using namespace std;
vector<int>G[MAX_V];//这里用不定长数组，来存图。 
int V,E,color[MAX_V];
bool dfs(int v,int c)
{
    color[v] = c;
    for(int i=0;i<G[v].size();i++){//连接这个节点的所有节点 
        if(color[G[v][i]] == c) return false;
        if(color[G[v][i]] == 0 && !dfs(G[v][i],-c)) return false;
        /*注意这一步，不能分解，因为当该层的下一层，返回false时，到递归回到这一层仍要返回false。*/ 
    }
    return true;
}
void solve()
{
    if(!dfs(0,1))
    {//本题是从0这个节点来搜索就可，但有些题目，图可能不是联通的，故要从头到尾遍历一遍。 
        printf("NOT BICOLORABLE.\n");
        return;
    }
 
    printf("BICOLORABLE.\n");
    return;
}
int main(void)
{
    while(~scanf("%d",&V))
    {
        scanf("%d",&E);
        memset(color,0,sizeof(color));
        memset(G,0,sizeof(G));
        int a,b;
        for(int i=0;i<E;i++)
        {
            scanf("%d %d",&a,&b);//注意是无向图
            G[a].push_back(b);
            G[b].push_back(a);
        }
        solve();
    }
    return 0;
}

2.P1155 双栈排序（二分图的染色判断+链式前向星）

P1155 双栈排序

P1155 双栈排序（二分图的染色判断+链式前向星）

注：如果您通过本文,有(qi)用(guai)的知识增加了，请您点个赞再离开,如果不嫌弃的话,点个关注再走吧 ! 当然，也欢迎在讨论区指出此文的不足处，作者会及时对文章加以修正 !