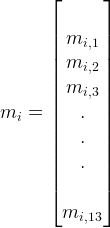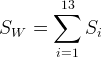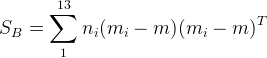LDA数据压缩原理及python应用（葡萄酒案例分析）
目录
线性判别分析（LDA）数据降维及案例实战
一、LDA是什么
二、计算散布矩阵
三、线性判别式及特征选择
四、样本数据降维投影
五、完整代码
结语
线性判别分析（LDA）数据降维及案例实战
一、LDA是什么
- LDA概念及与PCA区别
LDA线性判别分析（Linear Discriminant Analysis）也是一种特征提取、数据压缩技术。在模型训练时候进行LDA数据处理可以提高计算效率以及避免过拟合。它是一种有监督学习算法。
与PCA主成分分析（Principal Component Analysis）相比，LDA是有监督数据压缩方法，而PCA是有监督数据压缩及特征提取方法。PCA目标是寻找数据集最大方差方向作为主成分，LDA目标是寻找和优化具有可分性特征子空间。其实两者各有优势，更深入详细的区分和应用等待之后的学习，这里我仍然以葡萄酒数据集分类为案例记录原理知识的学习和具体实现步骤。
对比我之前记录的PCA请看：PCA数据降维原理及python应用（葡萄酒案例分析）
- LDA内部逻辑实现步骤
- 标准化d维数据集。
- 计算每个类别的d维均值向量。
- 计算跨类散布矩阵
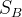和类内散布矩阵 
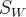. - 线性判别式及特征计算。
- 按特征值降序排列，与对应的特征向量成对排序。
- 选择最具线性判别性的前k个特征，构建变换矩阵
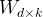. - 通过变换矩阵将原数据投影至k维子空间。
二、计算散布矩阵
1、数据集下载
下载葡萄酒数据集wine.data到本地，或者到时在加载数据代码是从远程服务器获取，为了避免加载超时推荐下载本地数据集。
下载之后用记事本打开wine.data可见得，第一列为葡萄酒数据类别标签，共有3类，往后的13列为特征值。
数据加载以及标准化数据处理与PCA技术一样，具体可以翻看PCA数据降维原理及python应用（葡萄酒案例分析），或者本文第五部分完整代码有具体实现代码。
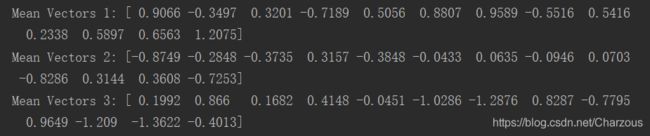
2、计算散布矩阵第一步，先计算每个类别每个样本的均值向量。
公式： 
, i =1,2,3 表示类别，每个特征取平均值。
得到三个均值向量为： 
代码实现：
# 计算均值向量
np.set_printoptions(precision=4)
mean_vecs = []
for label in range(1, 4):
mean_vecs.append(np.mean(x_train_std[y_train == label], axis=0))打印查看结果：
3、计算类内散布矩阵。
每个样本 i 的散布矩阵：
类内散布矩阵即每个样本的累加：
代码实现：
# 计算类内散布矩阵
k = 13
Sw = np.zeros((k, k))
for label, mv in zip(range(1, 4), mean_vecs):
Si = np.zeros((k, k))
Si = np.cov(x_train_std[y_train == label].T)
Sw += Si
print("类内散布矩阵：",Sw.shape[0],"*",Sw.shape[1])矩阵规模：
4、计算跨类散布矩阵。
公式：
公式中，m是所有样本总均值向量，也就是不分类的情况下计算特征平均值。
代码实现：
# 计算跨类散布矩阵
mean_all = np.mean(x_train_std, axis=0)
Sb = np.zeros((k, k))
for i, col_mv in enumerate(mean_vecs):
n = x_train[y_train == i + 1, :].shape[0]
col_mv = col_mv.reshape(k, 1) # 列均值向量
mean_all = mean_all.reshape(k, 1)
Sb += n * (col_mv - mean_all).dot((col_mv - mean_all).T)三、线性判别式及特征选择
LDA其他步骤与PCA相似，但是，PCA是分解协方差矩阵提取特征值，LDA则是求解矩阵 
得到广义特征值，实现：
# 计算广义特征值
eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(Sw).dot(Sb))
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)对特征值降序排列之后，打印看看：
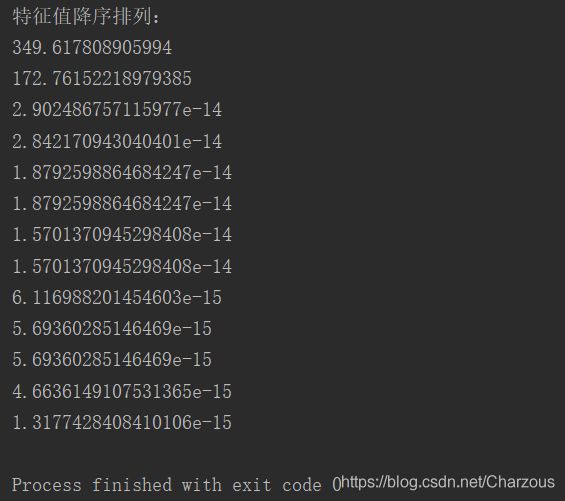
print("特征值降序排列：")
for eigen_val in eigen_pairs:
print(eigen_val[0])
从捕捉到的特征值发现，前两个可以占据大部分数据集特征了，接下来可视化表示更加直观地观察：
# 线性判别捕捉，计算辨识力
tot = sum(eigen_vals.real)
discr = []
# discr=[(i/tot) for i in sorted(eigen_vals.real,reverse=True)]
for i in sorted(eigen_vals.real, reverse=True):
discr.append(i / tot)
# print(discr)
cum_discr = np.cumsum(discr) # 计算累加方差
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
plt.bar(range(1,14),discr,alpha=0.5,align='center',label='独立辨识力')
plt.step(range(1,14),cum_discr,where='mid',label='累加辨识力')
plt.ylabel('"辨识力"比')
plt.xlabel('线性判别')
plt.ylim([-0.1,1.1])
plt.legend(loc='best')
plt.show()
很明显，最具线性判别的前两个特征捕捉了100%的信息，下面以此构建变换矩阵 W.
四、样本数据降维投影
构建变换矩阵：
# 变换矩阵
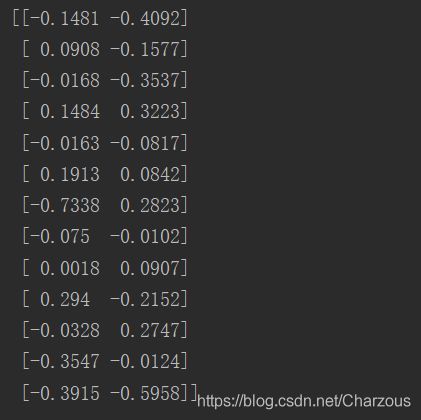
w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real, eigen_pairs[1][1][:, np.newaxis].real))
print(w)来瞅瞅，这就是前两个特征向量的矩阵表示。
现在有了变换矩阵，就可以将样本训练数据投影到降维特征空间了：
. 并展示分类结果：
# 样本数据投影到低维空间
x_train_lda = x_train_std.dot(w)
colors = ['r', 'g', 'b']
marks = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, marks):
plt.scatter(x_train_lda[y_train == l, 0],
x_train_lda[y_train == l, 1] * -1,
c=c, label=l, marker=m)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
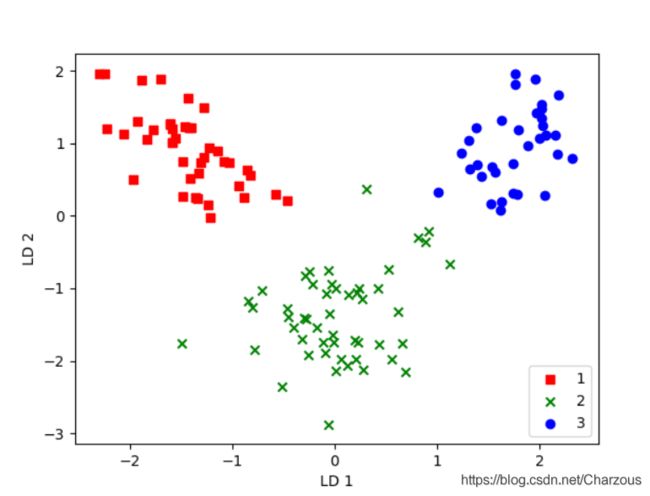
plt.legend(loc='lower right')
plt.show()
很明显，三个类别线性可分，效果也不错，相比较PCA方法，我感觉LDA分类结果更好，我们知道，LDA是有监督的方法，有利用到数据集的标签。
五、完整代码
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# load data
df_wine = pd.read_csv('D:\\PyCharm_Project\\maching_learning\\wine_data\\wine.data', header=None) # 本地加载
# df_wine=pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=None)#服务器加载
# split the data，train：test=7:3
x, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, stratify=y, random_state=0)
# standardize the feature 标准化单位方差
sc = StandardScaler()
x_train_std = sc.fit_transform(x_train)
x_test_std = sc.fit_transform(x_test)
# 计算均值向量
np.set_printoptions(precision=4)
mean_vecs = []
for label in range(1, 4):
mean_vecs.append(np.mean(x_train_std[y_train == label], axis=0))
# print("Mean Vectors %s:" % label,mean_vecs[label-1])
# 计算类内散布矩阵
k = 13
Sw = np.zeros((k, k))
for label, mv in zip(range(1, 4), mean_vecs):
Si = np.zeros((k, k))
# for row in x_train_std[y_train==label]:
# row,mv=row.reshape(n,1),mv.reshape(n,1)
# Si+=(row-mv).dot((row-mv).T)
Si = np.cov(x_train_std[y_train == label].T)
Sw += Si
# print("类内散布矩阵：",Sw.shape[0],"*",Sw.shape[1])
# print("类内标签分布：",np.bincount(y_train)[1:])
# 计算跨类散布矩阵
mean_all = np.mean(x_train_std, axis=0)
Sb = np.zeros((k, k))
for i, col_mv in enumerate(mean_vecs):
n = x_train[y_train == i + 1, :].shape[0]
col_mv = col_mv.reshape(k, 1) # 列均值向量
mean_all = mean_all.reshape(k, 1)
Sb += n * (col_mv - mean_all).dot((col_mv - mean_all).T)
# print("跨类散布矩阵：", Sb.shape[0], "*", Sb.shape[1])
# 计算广义特征值
eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(Sw).dot(Sb))
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
# print(eigen_pairs[0][1][:,np.newaxis].real) # 第一特征向量
# print("特征值降序排列：")
# for eigen_val in eigen_pairs:
# print(eigen_val[0])
# 线性判别捕捉，计算辨识力
tot = sum(eigen_vals.real)
discr = []
# discr=[(i/tot) for i in sorted(eigen_vals.real,reverse=True)]
for i in sorted(eigen_vals.real, reverse=True):
discr.append(i / tot)
# print(discr)
cum_discr = np.cumsum(discr) # 计算累加方差
# plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
# plt.bar(range(1,14),discr,alpha=0.5,align='center',label='独立辨识力')
# plt.step(range(1,14),cum_discr,where='mid',label='累加辨识力')
# plt.ylabel('"辨识力"比')
# plt.xlabel('线性判别')
# plt.ylim([-0.1,1.1])
# plt.legend(loc='best')
# plt.show()
# 转换矩阵
w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real, eigen_pairs[1][1][:, np.newaxis].real))
# print(w)
# 样本数据投影到低维空间
x_train_lda = x_train_std.dot(w)
colors = ['r', 'g', 'b']
marks = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, marks):
plt.scatter(x_train_lda[y_train == l, 0],
x_train_lda[y_train == l, 1] * -1,
c=c, label=l, marker=m)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower right')
plt.show()
结语
这篇记录了这几天学习的LDA实现数据降维的方法，仍然以葡萄酒数据集为案例，在上面一步步的拆分中，我们更加清楚线性判别分析LDA方法的内部实现，在这个过程，对于初步学习的我感觉能够认识和理解更深刻，当然以后数据处理使用LDA方法时候会用到一些第三方库的类，实现起来更加方便，加油学习，期待下一篇LDA实现更简洁的方法！
我的博客园：LDA线性判别分析原理及python应用（葡萄酒案例分析）
我的CSDN博客：https://blog.csdn.net/Charzous/article/details/108007441