LDA与PCA数据降维算法理论与实现(基于python)
数据降维
一、 线性判别分析(LDA)
linear Discriminant Analysis
用途:
数据预处理中的降维,分类任务
目标:
LDA关心的是能够最大化类间区分度的坐标轴成分
将特征空间(数据集中的多位样本)投影到一个维度更加小的Kw维子空间中,同时保持区分类别的信息
原理
投影到维度更低的空间,使得投影后的点,会形成按照类别区分,一簇一簇的情况,相同类别的点,将会在投影后的空间中更接近方法
监督性:LDA是‘有监督’的,它的计算是另一类特定的方向
投影:找到更合适分类的空间
与PCA不同,更关心分类而不是方差
数学原理
原始数据
变换数据
目标
找到投影该投影: y = w T ∗ x y = w^{T} * x y=wT∗x
LDA分类的一个目标是使得不同类别之间的距离越远越好,
同一个类别之间的距离越近越好
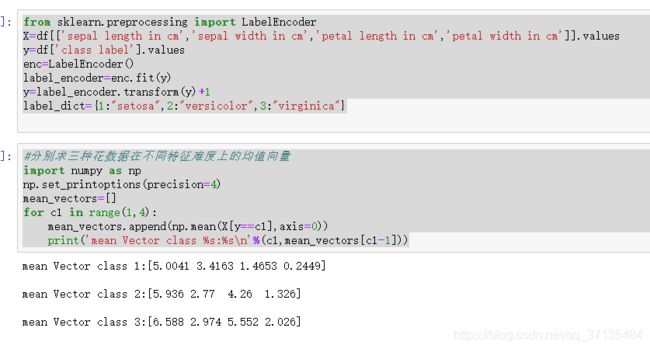
每类样例的均值: μ i = 1 N i ∑ x ∈ ω i x \mu_{i} = \frac{1}{N_{i}}\sum_{x \in \omega_{i}} x μi=Ni1∑x∈ωix
投影后的均值: μ i ~ = 1 N i ∑ x ∈ ω i y = 1 N i ∑ x ∈ ω i w T ∗ x = w T μ i \widetilde{\mu_{i}}=\frac{1}{N_{i}}\sum_{x \in \omega_{i}} y = \frac{1}{N_{i}}\sum_{x \in \omega_{i}} w^{T} * x = w^{T}\mu_{i} μi =Ni1∑x∈ωiy=Ni1∑x∈ωiwT∗x=wTμi
投影后的两类样本中心点尽量分离:
J ( w ) = ∣ μ 1 ~ − μ 2 ~ ∣ = ∣ w T ( μ 1 − μ 2 ) ∣ J(w) = |\widetilde{\mu_{1}}-\widetilde{\mu_{2}}| = |w^T(\mu_{1}-\mu_{2})| J(w)=∣μ1 −μ2 ∣=∣wT(μ1−μ2)∣
不仅是要考虑最大化 J ( w ) J(w) J(w)
还有 散列值 μ i \mu_{i} μi(样本的密集程度,值越大,越分散,反之,越集中)
同类之间应该越密集些: μ i = 1 N i ∑ x ∈ ω i ( y − μ i ~ ) 2 \mu_{i} = \frac{1}{N_{i}}\sum_{x \in \omega_{i}}(y-\widetilde{\mu_{i}})^2 μi=Ni1∑x∈ωi(y−μi )2
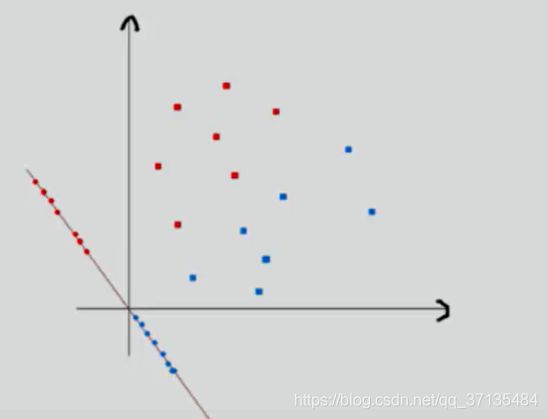
如下图,如果映射到X1轴上,数据较为分散,而且红色的数据簇和蓝色的数据簇会重合,无法分开,而投影到X2轴上虽然 J ( w J(w J(w小了,可是数据却比较集中,分类效果相对于X1轴会比较好
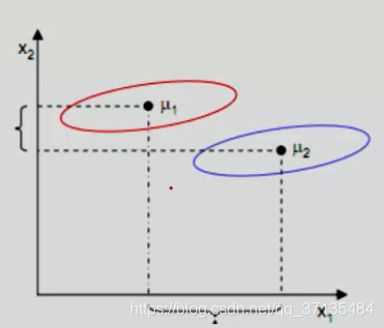
目标函数: j ( w ) = ∣ μ 1 ~ − μ 2 ~ ∣ 2 S 1 ~ 2 + S 2 ~ 2 {j(w)}=\frac{|\widetilde{\mu_{1}}-\widetilde{\mu_{2}}|^2}{\widetilde{S_{1}}^2+\widetilde{S_{2}}^2} j(w)=S1 2+S2 2∣μ1 −μ2 ∣2
散列值公式展开: S i ~ 2 = ∑ y ∈ ω i ( y − μ i ~ ) 2 = ∑ x ∈ ω i ( w T x − w T μ i ) 2 = ∑ x ∈ ω i ( x − μ i ) ( x − μ i ) T w \widetilde{S_{i}}^2=\sum_{y \in \omega_{i}}(y-\widetilde{\mu_{i}})^2=\sum_{x\in\omega_{i}}(w^Tx-w^T\mu_{i})^2=\sum_{x\in\omega_{i}}(x-\mu_{i})(x-\mu_{i})^Tw Si 2=∑y∈ωi(y−μi )2=∑x∈ωi(wTx−wTμi)2=∑x∈ωi(x−μi)(x−μi)Tw
散列矩阵(scatter matrices):
S i = ∑ x ∈ ω i ( x − μ i ) ( x − μ i ) T S_{i}=\sum_{x\in\omega_{i}}(x-\mu_{i})(x-\mu_{i})^T Si=∑x∈ωi(x−μi)(x−μi)T
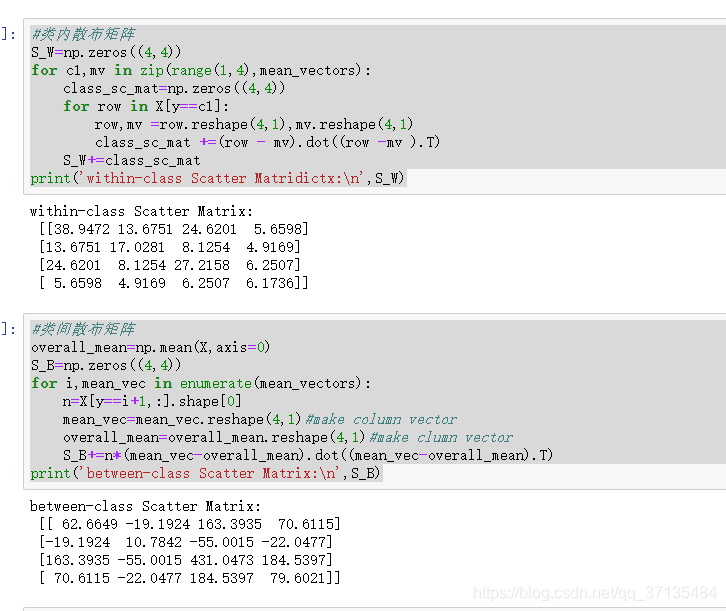
**类内散布矩阵 S w = S 1 + S 2 S_{w}=S_{1}+S_{2} Sw=S1+S2:
S i ~ 2 = w T S i w \widetilde{S_{i}}^2=w^TS_{i}w Si 2=wTSiw ======> s 1 ~ 2 + s 2 ~ 2 = w T S w w \widetilde{s_{1}}^2+\widetilde{s_{2}}^2=w^TS_{w}w s1 2+s2 2=wTSww
目标函数: J ( w ) = ∣ μ 1 ~ − μ 2 ~ ∣ 2 = w T ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T w = w T S B w J(w)=|\widetilde{\mu_{1}}-\widetilde{\mu_{2}}|^2=w^T(\mu_{1}-\mu_{2})(\mu_{1}-\mu_{2})^Tw=w^TS_{B}w J(w)=∣μ1 −μ2 ∣2=wT(μ1−μ2)(μ1−μ2)Tw=wTSBw
S B S_{B} SB称为类间散布矩阵
最终目标函数: J ( w ) = w T S B w w T S w w J(w)=\frac{w^TS_{B}w}{w^TS_{w}w} J(w)=wTSwwwTSBw
不过,如果分子分母都是可以取任意值的,那就会使得有无穷解,我们将分母限制为长度为1
根据拉格朗日乘子法:
c ( w ) = w T S B w − λ ( w T S w w − 1 ) = > d c d w = 2 S B w − 2 λ S w w = = > S b w = λ S w w c(w)=w^TS_{B}w-\lambda(w^TS_{w}w-1) =>\frac{dc}{dw}=2S_{B}w-2\lambda S_{w}w==>S_{b}w=\lambda S_{w}w c(w)=wTSBw−λ(wTSww−1)=>dwdc=2SBw−2λSww==>Sbw=λSww
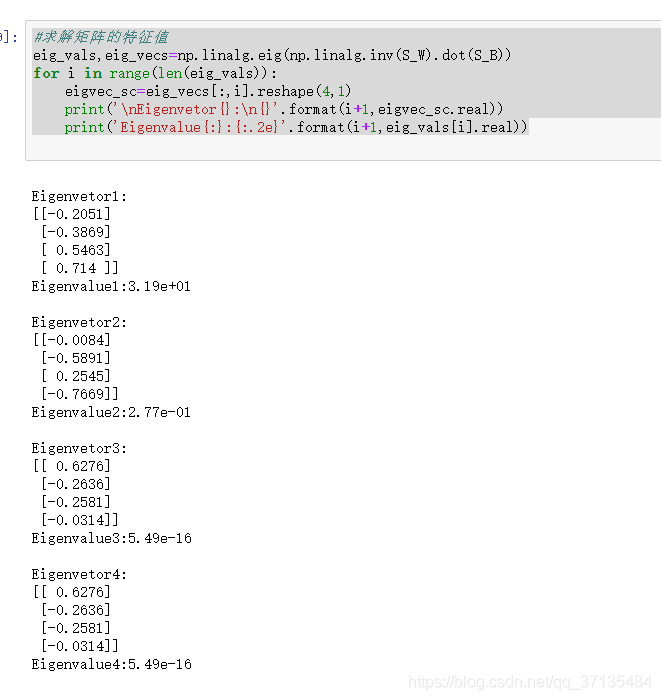
两边都乘以 S w 的 逆 : S_{w}的逆: Sw的逆: S w − 1 S B w = λ w S_{w}^{-1}S_{B}w=\lambda w Sw−1SBw=λw(w就是矩阵 S w − 1 S B S_{w}^{-1}S_{B} Sw−1SB的特征向量)
二、主成分分析(PCA)
PCA(Principal Component Analysis)降维中最常用的一种手段为了提取最有价值的信息(基于方差)降维后,数据的物理意义就被模糊化了,此时可以通过数据降维来隐藏数据的真实信息。
基本数学概念
向量的表示及基变换
内积: ( a 1 , a 2 , . . . , a n ) ⋅ ( b 1 , b 2 , . . . , b n ) = a 1 b 1 + a 2 b 2 + . . . + a n b n (a_{1},a_{2},...,a_{n})\cdot(b_{1},b_{2},...,b_{n})=a_{1}b_{1}+a_{2}b_{2}+...+a_{n}b_{n} (a1,a2,...,an)⋅(b1,b2,...,bn)=a1b1+a2b2+...+anbn
也就是: A ⋅ B = ∣ A ∣ ∣ B ∣ c o s ( a ) A\cdot B=|A||B|cos(a) A⋅B=∣A∣∣B∣cos(a) ,设向量B的模为1,则A与B的模为1,则A与B的内积等于A所在直线投影的矢量长度

向量可以表示为(3,2)实际上表示线性组合: x ( 1 , 0 ) T + y ( 0 , 1 ) T x(1,0)^T+y(0,1)^T x(1,0)T+y(0,1)T
基:(0,1)和(1,0)叫做二维空间中的一组基
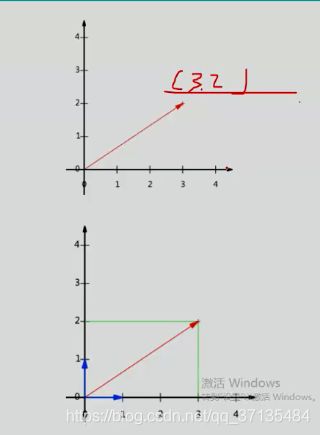
基变换: 基是正交的(即内积为0,或者直观的说互相垂直)且线性无关
变换: 数据与一个基做内积运算,结果作为第一个新的坐标分量,然后与第二个基做内积运算,结果作为第二个新坐标的分量如数据(3,2)映射到基中坐标:
( 1 2 1 2 − 1 2 1 2 ) ( 3 2 ) = ( 5 2 − 1 2 ) ( \begin{matrix} \frac{1}{ \sqrt{2}} & \frac{1}{ \sqrt{2}} \\ -\frac{1}{ \sqrt{2}} & \frac{1}{ \sqrt{2}} \end{matrix}) (\begin{matrix}3\\2\end{matrix})=(\begin{matrix} \frac{5}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}\end{matrix}) (21−212121)(32)=(25−21)

两个矩阵相乘的意义是将右边矩阵中你的每一列列向量变换到左边矩阵中每一行行向量为基表示的空间去
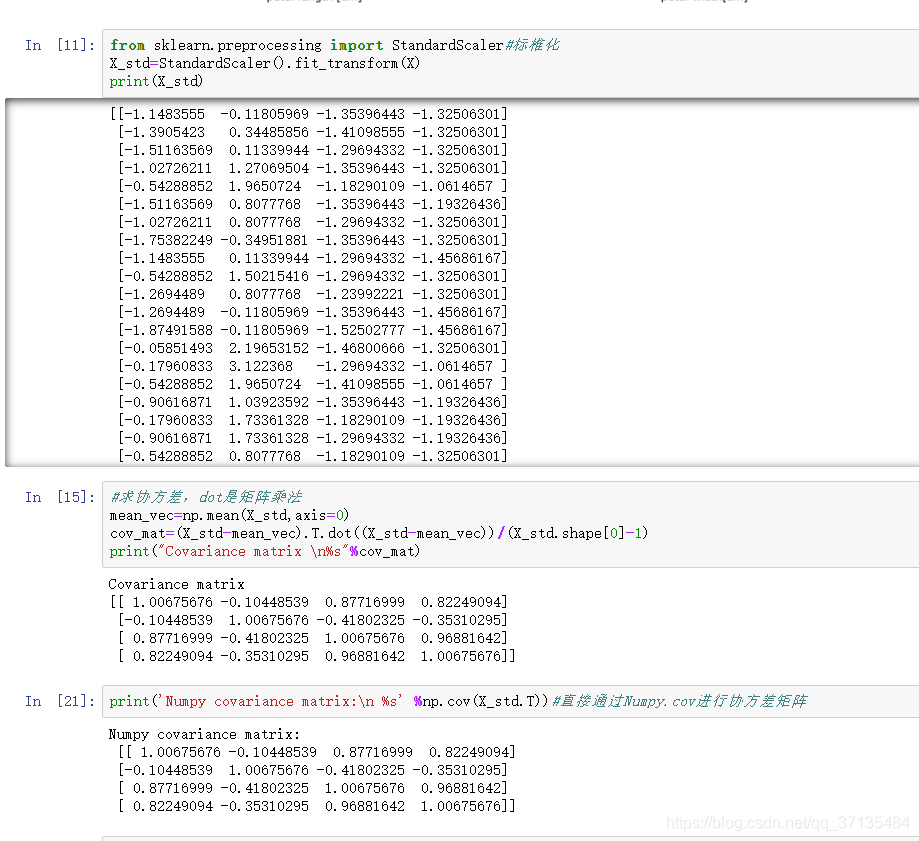
协方差矩阵
方向: 如何选择这个方向(基)才能尽量保留最多的原始信息呢?一种直观的看法是:洗完投影值尽可能分散
方差: V a r ( a ) = 1 m ∑ i = 1 m ( a i − μ ) 2 Var(a)=\frac{1}{m}\sum_{i=1}^{m}(a_{i}-\mu)^2 Var(a)=m1∑i=1m(ai−μ)2
寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大
协方差
协方差(假设均值为0时): C o v ( a , b ) = 1 m ∑ i = 1 m a i b i Cov(a,b)=\frac{1}{m}\sum_{i=1}^{m}a_{i}b_{i} Cov(a,b)=m1∑i=1maibi
如果单纯只选择方差最大的方向,后续方向应该会和方差最大的方向接近重合。
解决方法: 为了让两个字段尽可能的表示更加多的原始信息,不希望他们之间存在(线性)相关性的,可以使用两个字段的协方差表示其相关性 C o v ( a , b ) = ∑ i = 1 m a i b i Cov(a,b)=\sum_{i=1}^{m}a_{i}b_{i} Cov(a,b)=∑i=1maibi
当协方差为0时,表示两个字段完全独立。为了让协方差为0,选择第二个基时只能在与第一个基正交的方向上选择。因此最终选择两个方向一定是正交的(第一个2基在方差最大的方向上。第二个基与第一个基正交)。
优化目标
将一组N维向量降为K维(K大于0,小于N),目标是选择K个单位正交基,使原始数据变换到这组基后,各字段两两间协方差为0,字段的方差尽可能大
协方差矩阵: X = ( a 1 a 2 . . . a m b 1 b 2 . . . b m ) X=\left(\begin{matrix} a_{1}&a_{2}&...&a_{m}\\b_{1}&b_{2}&...&b_{m}\end{matrix}\right) X=(a1b1a2b2......ambm)
1 m X X T = ( 1 m ∑ i = 1 m a i 2 1 m ∑ i = 1 m a i b i 1 m ∑ i = 1 m a i b i 1 m ∑ i = 1 m b i 2 ) \frac{1}{m}XX^T=\left(\begin{matrix} \frac{1}{m}\sum_{i=1}^{m}a_{i}^{2}& \frac{1}{m}\sum_{i=1}^{m}a_{i}b_{i}\\ \frac{1}{m}\sum_{i=1}^{m}a_{i}b_{i}& \frac{1}{m}\sum_{i=1}^{m}b_{i}^{2}\end{matrix}\right) m1XXT=(m1∑i=1mai2m1∑i=1maibim1∑i=1maibim1∑i=1mbi2)
矩阵对角线的两个元素分别是两个字段的方差,而其它元素是a和b的协方差。
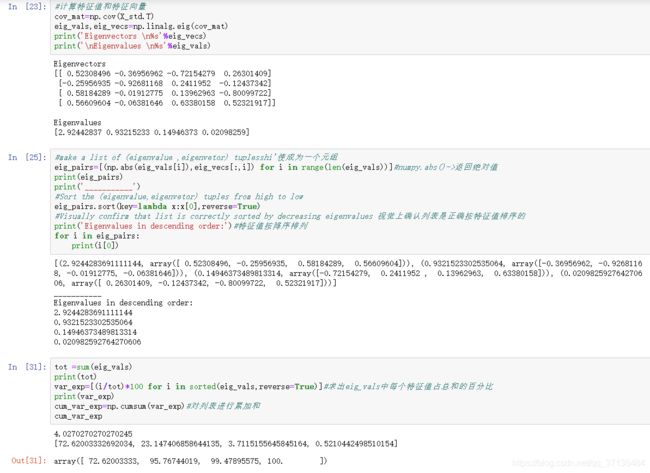
协方差矩阵对角化: 即除对角线外其它的元素化为0,并且在对角线上将元素按大小从上到下排列
协方差矩阵对角化: P C P T = Λ = ( λ 1 λ 2 ⋱ λ n ) PCP^T=\Lambda=\left(\begin{matrix}\lambda_{1}& &\\&&\lambda_{2}\\&& &\ddots\\&&&&\lambda_{n}\end{matrix}\right) PCPT=Λ=⎝⎜⎜⎛λ1λ2⋱λn⎠⎟⎟⎞
实对称矩阵:一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量
E = ( e 1 e 2 ⋯ e n ) E=\left(\begin{matrix}e_{1}&e_{2}&\cdots&e_{n}\end{matrix}\right) E=(e1e2⋯en)
实对称矩阵可进行对角化:
E C E T = Λ = ( λ 1 λ 2 ⋱ λ n ) ECE^T=\Lambda=\left(\begin{matrix}\lambda_{1}& &\\&&\lambda_{2}\\&& &\ddots\\&&&&\lambda_{n}\end{matrix}\right) ECET=Λ=⎝⎜⎜⎛λ1λ2⋱λn⎠⎟⎟⎞
根据特征值得我从大到小,将特征向量从上到下排列,则用前K行组成的矩阵乘以原始数据矩阵X,就得到了我们需要降维后的数据矩阵Y

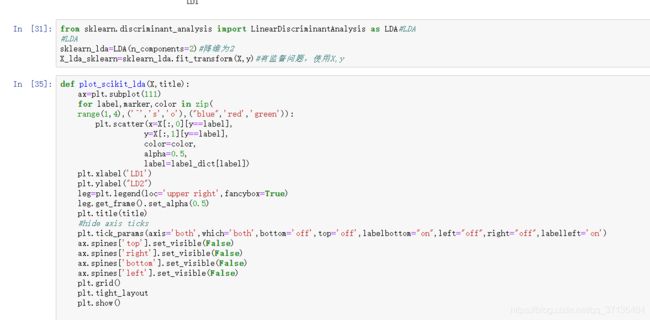
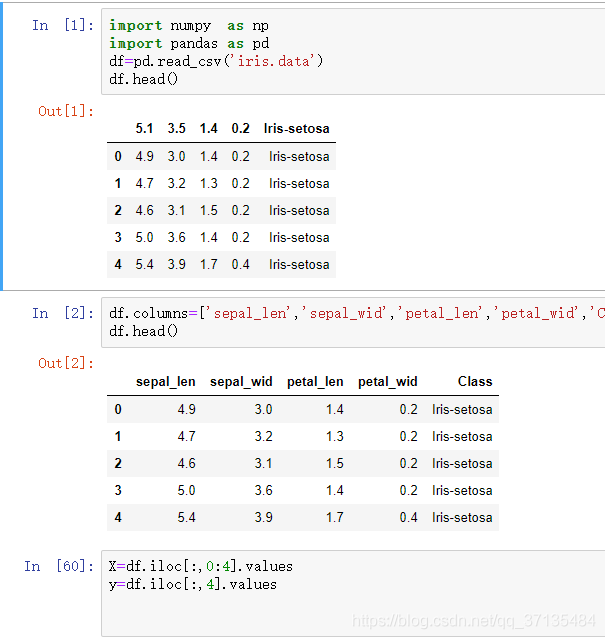
三、python实现
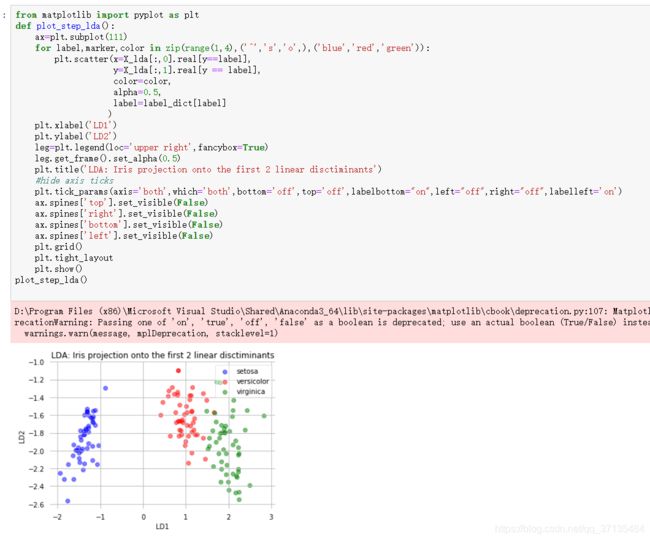
基于python的LDA和PCA实例(自己实现和调用现成的库)jupyter源码:
https://download.csdn.net/download/qq_37135484/11579884