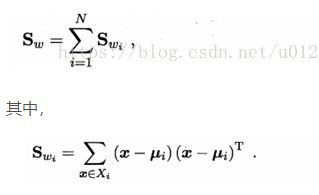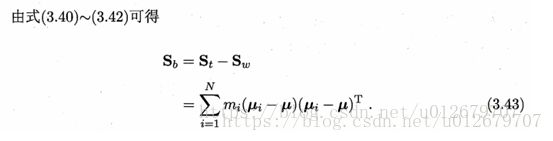【机器学习】python实现LDA多类问题
【机器学习】python实现LDA多类问题
1.读取数据集
2.进行LDA特征提取
2.1 将样本分类
2.2 求类内散度矩阵
2.3求类间散度矩阵
2.4 计算Sw-1*Sb的特征值和特征矩阵
2.5 特征值排序，提取前k个特征向量
关于LDA的原理已经在之前讲过了，详情可戳：【机器学习】LDA线性判别分析
本节主要用python实现LDA推广到多类的问题。
【注意】本文的运行环境是windows+Pycharm+python3.6。
【参考】线性判别分析(LDA)和python实现（多分类问题）https://blog.csdn.net/z962013489/article/details/79918758
LDA算法流程:
1.读取数据集
#1.读取数据集
iris = load_iris()
X = iris.data
y = iris.target
注意：读取到的X,y均为矩阵类型
>>> type(X)
2.进行LDA特征提取
#2.LDA特征提取
W=LDA_reduce_dimension(X, y, 2) #得到投影矩阵
newX=np.dot(X,W)# (m*n) *(n*k)=m*k下面,详细介绍ＬＤＡ算法实现过程:
2.1 将样本分类
def LDA_reduce_dimension(X,y,nComponents):
'''
输入：X为数据集(m*n)，y为label(m*1)，nComponents为目标维数
输出：W 矩阵（n * nComponents）
'''
#y1= set(y) #set():剔除矩阵y里的重复元素,化为集合的形式
labels=list(set(y)) #list():将其转化为列表
#将样本分类
xClasses={} #字典
for label in labels:
xClasses[label]=np.array([ X[i] for i in range(len(X)) if y[i]==label ]) #list解析 其中， set()是转化为集合形式，这样可剔除类别中的重复元素。list()是将其转化为列表，便于后续操作。
labels=list(set(y))
#set():剔除矩阵y里的重复元素,化为集合的形式
#list():将其转化为列表set()和list()的实例如下：
labels=list(set(y)) #list():将其转化为列表
"""
eg:
>>> a=[3,2,1,2]
>>> set(a)
{1, 2, 3}
>>> list(set(a))
[1, 2, 3]
>>> e=set(a)
>>> type(e)
#集合
>>> f=list(e)
>>> type(f)
#列表
""" 注意，list解析部分，此处非常灵活。可通过下边的例子进行理解。
"""
x=[1,2,3,4]
y=[5,6,7,8]
我想让着两个list中的偶数分别相加，应该结果是2+6,4+6,2+8,4+8
下面用一句话来写:
>>>[a + b for a in x for b in y if a%2 == 0 and b%2 ==0] #list解析
"""2.2 求类内散度矩阵
表达式如下：
#求类内散度矩阵
# Sw=sum(np.dot((Xi-ui).T, Xi-ui)) i=1...m
Sw=np.zeros((len(meanAll), len(meanAll) )) # n*n
for i in labels:
Sw+=np.dot( (xClasses[i]-meanClasses[i]).T, (xClasses[i]-meanClasses[i]) )
2.3求类间散度矩阵
类间散度矩阵Sb 可以通过 全局散度矩阵St 和 类内散度矩阵Sw 来求。
#全局散度矩阵
St=np.zeros((len(meanAll), len(meanAll) ))
St=np.dot((X - meanAll).T, X - meanAll)
#求类内散度矩阵
# Sw=sum(np.dot((Xi-ui).T, Xi-ui)) i=1...m
Sw=np.zeros((len(meanAll), len(meanAll) )) # n*n
for i in labels:
Sw+=np.dot( (xClasses[i]-meanClasses[i]).T, (xClasses[i]-meanClasses[i]) )
#求类间散度矩阵
Sb = np.zeros((len(meanAll), len(meanAll))) # n*n
Sb=St-Swnp.dot()矩阵乘法的具体实例如下：
"""
np.dot()
Examples
--------
>>> np.dot(3, 4) #标量相乘
12
Neither argument is complex-conjugated:
>>> np.dot([2j, 3j], [2j, 3j]) #两个一维向量相乘
(-13+0j)
For 2-D arrays it is the matrix product: #两个二维矩阵相乘
>>> a = [[1, 0], [0, 1]]
>>> b = [[4, 1], [2, 2]]
>>> np.dot(a, b)
array([[4, 1],
[2, 2]])
>>> a = np.arange(3*4*5*6).reshape((3,4,5,6))
>>> b = np.arange(3*4*5*6)[::-1].reshape((5,4,6,3))
>>> np.dot(a, b)[2,3,2,1,2,2]
499128
>>> sum(a[2,3,2,:] * b[1,2,:,2])
499128
"""2.4 计算Sw-1*Sb的特征值和特征矩阵
# 计算Sw-1*Sb的特征值和特征矩阵
eigenValues,eigenVectors=np.linalg.eig(
np.dot( np.linalg.inv(Sw), Sb)
)
2.5 特征值排序，提取前k个特征向量
#提取前nComponents个特征向量
sortedIndices=np.argsort(eigenValues) #特征值排序
W=eigenVectors[:,sortedIndices[:-nComponents-1:-1] ] # 提取前nComponents个特征向量
return W排序函数np.argsort( )的具体功能如下:
"""
np.argsort()
eg:
>>> x = np.array([3, 1, 2])
>>> np.argsort(x)
array([1, 2, 0])
Two-dimensional array:
>>> x = np.array([[0, 3], [2, 2]])
>>> x
array([[0, 3],
[2, 2]])
>>> np.argsort(x, axis=0)
array([[0, 1],
[1, 0]])
>>> np.argsort(x, axis=1)
array([[0, 1],
[0, 1]])
"""
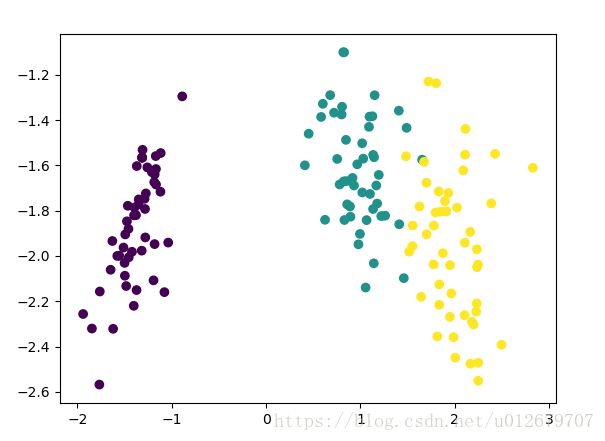
最终分类结果如下：
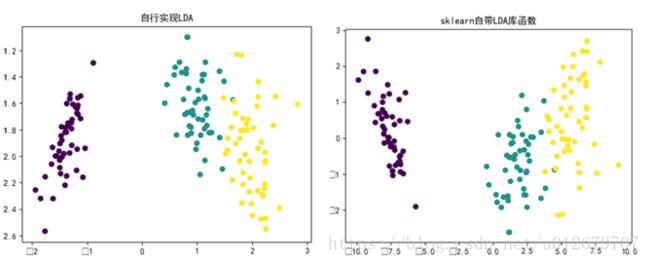
与sklearn自带的LDA函数的运行结果相对比如下：（左图为自己实现，右图为sklearn库函数）
附全部代码：
# -*- coding:utf-8 -*-
"""
@author:Lisa
@file:svm_Iris.py
@func:Use LDA to achieve Iris flower feature extraction
@time:2018/6/1 0030上午 9:58
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import load_iris
import matplotlib
#define converts(字典)
def Iris_label(s):
it={b'Iris-setosa':0, b'Iris-versicolor':1, b'Iris-virginica':2 }
return it[s]
def LDA_reduce_dimension(X,y,nComponents):
'''
输入：X为数据集(m*n)，y为label(m*1)，nComponents为目标维数
输出：W 矩阵（n * nComponents）
'''
#y1= set(y) #set():剔除矩阵y里的重复元素,化为集合的形式
labels=list(set(y)) #list():将其转化为列表
"""
eg:
>>> a=[3,2,1,2]
>>> set(a)
{1, 2, 3}
>>> list(set(a))
[1, 2, 3]
>>> e=set(a)
>>> type(e)
#集合
>>> f=list(e)
>>> type(f)
#列表
"""
xClasses={} #字典
for label in labels:
xClasses[label]=np.array([ X[i] for i in range(len(X)) if y[i]==label ]) #list解析
"""
x=[1,2,3,4]
y=[5,6,7,8]
我想让着两个list中的偶数分别相加，应该结果是2+6,4+6,2+8,4+8
下面用一句话来写:
>>>[a + b for a in x for b in y if a%2 == 0 and b%2 ==0]
"""
#整体均值
meanAll=np.mean(X,axis=0) # 按列求均值，结果为1*n(行向量)
meanClasses={}
#求各类均值
for label in labels:
meanClasses[label]=np.mean(xClasses[label],axis=0) #1*n
#全局散度矩阵
St=np.zeros((len(meanAll), len(meanAll) ))
St=np.dot((X - meanAll).T, X - meanAll)
#求类内散度矩阵
# Sw=sum(np.dot((Xi-ui).T, Xi-ui)) i=1...m
Sw=np.zeros((len(meanAll), len(meanAll) )) # n*n
for i in labels:
Sw+=np.dot( (xClasses[i]-meanClasses[i]).T, (xClasses[i]-meanClasses[i]) )
# 求类间散度矩阵
Sb = np.zeros((len(meanAll), len(meanAll))) # n*n
Sb=St-Sw
#求类间散度矩阵
# Sb=sum(len(Xj) * np.dot((uj-u).T,uj-u)) j=1...k
# Sb=np.zeros((len(meanAll), len(meanAll) )) # n*n
# for i in labels:
# Sb+= len(xClasses[i]) * np.dot( (meanClasses[i]-meanAll).T.reshape(len(meanAll),1),
# (meanClasses[i]-meanAll).reshape(1,len(meanAll))
# )
# 计算Sw-1*Sb的特征值和特征矩阵
eigenValues,eigenVectors=np.linalg.eig(
np.dot( np.linalg.inv(Sw), Sb)
)
#提取前nComponents个特征向量
sortedIndices=np.argsort(eigenValues) #特征值排序
W=eigenVectors[:,sortedIndices[:-nComponents-1:-1] ] # 提取前nComponents个特征向量
return W
"""
np.argsort()
eg:
>>> x = np.array([3, 1, 2])
>>> np.argsort(x)
array([1, 2, 0])
Two-dimensional array:
>>> x = np.array([[0, 3], [2, 2]])
>>> x
array([[0, 3],
[2, 2]])
>>> np.argsort(x, axis=0)
array([[0, 1],
[1, 0]])
>>> np.argsort(x, axis=1)
array([[0, 1],
[0, 1]])
"""
if '__main__'== __name__:
#1.读取数据集
iris = load_iris()
X = iris.data
y = iris.target
#2.LDA特征提取
W=LDA_reduce_dimension(X, y, 2) #得到投影矩阵
newX=np.dot(X,W)# (m*n) *(n*k)=m*k
#3.绘图
# 指定默认字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
plt.figure(1)
plt.scatter(newX[:,0],newX[:,1],c=y,marker='o') #c=y,
plt.title('自行实现LDA')
#4.与sklearn自带库函数对比
lda_Sklearn=LinearDiscriminantAnalysis(n_components=2)
lda_Sklearn.fit(X,y)
newX1=lda_Sklearn.transform(X)
plt.figure(2)
plt.scatter(newX1[:, 0], newX1[:, 1], marker='o', c=y)
plt.title('sklearn自带LDA库函数')
plt.show()