机器学习笔记（三）-线性判别分析

原创不易，转载前请注明博主的链接地址：Blessy_Zhu https://blog.csdn.net/weixin_42555080
本次代码的环境：
运行平台： Windows
Python版本： Python3.x
IDE： PyCharm

一、 前言

在文章机器学习笔记（一）-线性回归中已经介绍了线性回归，文中提到，线性回归是最基本最简单的机器学习算法，但是，在打破线性回归的某一特性时会出现新的算法。正如文章机器学习笔记（二）-感知机中介绍的感知机，它是打破了线性中的全局非线性这一性质——它是将线性回归得出的值，作为激励函数的输入，进而进行二分类的一种算法。同样的，这次要介绍的线性判别分析也是打破了线性回归的这一性质。
线性判别分析（LDA： Linear Discriminant Analysis），还有一个很响亮的名字就叫做Fisher判别分析（FLD： Fisher’s Linear Discriminant）。说到Fisher，那必须先在此膜拜一下，然后，再沿着Fisher老先生的足迹，把他的思想走一遍。
　

二、 LDA核心思想及实现细节

LDA的核心思想是：类内小，类间大。

2.1 定性分析

该如何理解呢！请结合着下图理解：
　

所谓的“类内小，类间大“，就是，投影后类内方差最小，类间方差最大”，如上图所示：将二维数据，在一维进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。这样就可以很好地区分两类，进而分割。实际上，通过上面的过程也可以知道，通过LDA也可以进行数据的降维！！！降维！！！降维！！！。
　

• 对于二分类，这样继续扩展到p维：将p维的数据全部投影到一维的坐标上,如上图的Z轴，然后选定一个阈值threshold，当Z值>threshold时，则认为它属于“四角形”类，当Z值
• 对于k分类， LDA的核心思想依然不变：将带上标签的数据（点），通过投影的方法，投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近。要说明白LDA，首先得弄明白线性分类器(Linear Classifier)：因为LDA是一种线性分类器。对于K-分类的一个分类问题，会有K个线性函数：
  
  当满足条件：对于所有的j，都有Yk > Yj,的时候，我们就说x属于类别k。对于每一个分类，都有一个公式去算一个分值，在所有的公式得到的分值中，找一个最大的，就是所属的分类了。

2.2 定量分析

这样，就会遇到一个难题！——该如何去找一个这样的直线或者切平面呢？实际上，只要找到这个切平面的方向向量或者法向量就可以。
首先确定一下，目标，这个算法的最终目标是找到那个切平面或直线的方向向量或者法向量。也就是你求的最终的W值。这里还以二分类为例子，来一步步求得这个W值。
首先定义数据集和主要符号表示：

这里假设正类为C1类，负类为C2类；其中Xc1是属于C1的类，Xc2是属于C2的类。|Xc1|是C1类的个数，|Xc2|是C2类的个数。
这里面需要明确一点的是：对于任意样本Xi来说，假设投影方向是w向量，则Xi这个样本点在w向量的投影方向是wTXi（w的转置与Xi样本点的向量内积），且限定||w||=1.
具体的证明如下：
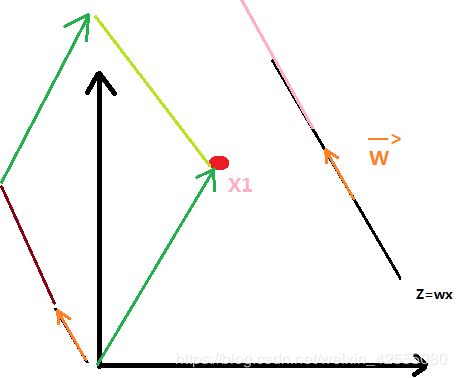
先看一下图，结合着图理解：
　

x1样本点（红色点），在Z=wx直线上的投影就是粉色线（其中Z直线的方向向量为W）。

既然，投影可以用wTXi表示，接下来工作就好做多了。
　

这样就可以通过求得使满足J(w)能够的最大的w，就可以找到使满足类内小，类间大的w向量，即：

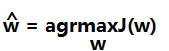
接下来，还是给出详细的步骤：
　

这一步主要是将样本点和代求量w带入到J(w)，为后来的进一步求w确定公式形式：
　

这里面定义了SB和Sw类间方差和类内方差：得到的次最终形式是

这如图的演示过程，我们最关心的是w的方向而不是，大小，所以凡是结果为具体值得成分全部去掉，这样可以得到最终的结果：

如果当类内方差的逆是单位矩阵时，最终w是

即：和C1类与C2类的平均差值有关。这样问题就可以得到解决。
你也许会问了——既然是要分为C1和C2类，为什么公式会直接就是用C1类和C2类的数据呢？如式子中的直接就用到了|Xc1| |Xc2|这样的数据！！！
实际上，机器学习算法的数据分为两部分，一部分是用来训练，目的就是找到参数，从而最终选出来代拟合的模型。第二部分是用来验证模型。对于训练的数据，实际上，它的所有信息都是已经知道的，也就是已经分好类了，我们可以直接拿来用就可以了。

2.3 多分类问题

假设类别变成多个了，那么要怎么改变，才能保证投影后类别能够分离呢？我们之前讨论的是如何将d维降到一维，现在类别多了，一维可能已经不能满足要求。假设我们有C个类别，可以将其投影到K个基向量。 具体做法就不再详细说明了，可参考文章：线性判别分析LDA详解

三、 LDA验证

3.1 数据生成

这里直接通过scikit-learn的接口来生成数据：

from sklearn.datasets import make_multilabel_classification
import numpy as np

x, y = make_multilabel_classification(n_samples=20, n_features=2,
                                      n_labels=1, n_classes=1,
                                      random_state=2)  # 设置随机数种子，保证每次产生相同的数据。

# 根据类别分个类
index1 = np.array([index for (index, value) in enumerate(y) if value == 0])  # 获取类别1的indexs
index2 = np.array([index for (index, value) in enumerate(y) if value == 1])  # 获取类别2的indexs

c_1 = x[index1]   # 类别1的所有数据(x1, x2) in X_1
c_2 = x[index2]  # 类别2的所有数据(x1, x2) in X_2
#print(c_1)
#print(c_2)

3.2 LDA算法实现

def cal_cov_and_avg(samples):
    """
    给定一个类别的数据，计算协方差矩阵和平均向量
    :param samples: 
    :return: 
    """
    u1 = np.mean(samples, axis=0)
    cov_m = np.zeros((samples.shape[1], samples.shape[1]))
    for s in samples:
        t = s - u1
        cov_m += t * t.reshape(2, 1)
    return cov_m, u1


def fisher(c_1, c_2):
    """
    fisher算法实现
    :param c_1: 
    :param c_2: 
    :return: 
    """
    cov_1, u1 = cal_cov_and_avg(c_1)
    cov_2, u2 = cal_cov_and_avg(c_2)
    s_w = cov_1 + cov_2
    u, s, v = np.linalg.svd(s_w)  # 奇异值分解
    s_w_inv = np.dot(np.dot(v.T, np.linalg.inv(np.diag(s))), u.T)
    return np.dot(s_w_inv, u1 - u2)

3.3 判定类别

def judge(sample, w, c_1, c_2):
    """
    true 属于1
    false 属于2
    :param sample:
    :param w:
    :param center_1:
    :param center_2:
    :return:
    """
    u1 = np.mean(c_1, axis=0)
    u2 = np.mean(c_2, axis=0)
    center_1 = np.dot(w.T, u1)
    center_2 = np.dot(w.T, u2)
    pos = np.dot(w.T, sample)
    return abs(pos - center_1) < abs(pos - center_2)


w = fisher(c_1, c_2)  # 调用函数，得到参数w
out = judge(c_1[1], w, c_1, c_2)   # 判断所属的类别
print(out)

3.4 绘图

import matplotlib.pyplot as plt

plt.scatter(c_1[:, 0], c_1[:, 1], c='#99CC99')
plt.scatter(c_2[:, 0], c_2[:, 1], c='#FFCC00')
line_x = np.arange(min(np.min(c_1[:, 0]), np.min(c_2[:, 0])),
                   max(np.max(c_1[:, 0]), np.max(c_2[:, 0])),
                   step=1)

line_y = - (w[0] * line_x) / w[1]
plt.plot(line_x, line_y)
plt.show()

最终如下图分别是样本为20,200,2000,20000时的结果：
　

四、总结

本篇内容主要介绍了LDA线性判别分析，并对LDA模型进行验证。这篇文章就到这里了，欢迎大佬们多批评指正，也欢迎大家积极评论多多交流。
　

　

参考文章

1 线性判别分析LDA详解
2 Fisher判别分析原理详解
3 机器学习(30)之线性判别分析(LDA)原理详解
4 机器学习中的数学(4)-线性判别分析（LDA）, 主成分分析(PCA)
5 python之实战----线性判别分析（LDA）战iris
6 fisher判别分析原理+python实现