文献阅读与复现（基于PCA图像重建和LDA的人脸识别）

基于PCA图像重建和LDA的人脸识别

Face recognition based on PCA image reconstruction and LDA

以下文字和代码大部分非原创，只为了一个记录留作备用复习的功能，侵删

一、散射矩阵

百度百科：散射矩阵是物理学中描述散射过程的一个主要观测量。假设散射源为很好的定域散射源，与被散射粒子的相互作用局限在有限的空间范围内，那么，无穷远时间以前粒子处于一个自由态，称为入态，无穷远时间之后粒子也是处于一个自由态，称为出态， 入态到初态，相互作用可以用一个矩阵描述，记为S，那么就有|Ψ>out=S |Ψ>in。这就是散射矩阵的定义。

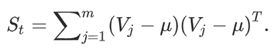
二、PCA

（1）概念

在许多领域的研究与应用中，通常需要对含有多个变量的数据进行观测，收集大量数据后进行分析寻找规律。多变量大数据集无疑会为研究和应用提供丰富的信息，但是也在一定程度上增加了数据采集的工作量。

因此需要找到一种合理的方法，在减少需要分析的指标同时，尽量减少原指标包含信息的损失，以达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系，因此可以考虑将关系紧密的变量变成尽可能少的新变量，使这些新变量是两两不相关的，那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。主成分分析与因子分析就属于这类降维算法。

降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。在实际的生产和应用中，降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。

PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

（2）PCA实验

下图是通过PCA最大方差算法得到的一副图像，其中蓝色点二维数组X = [(-1,1),(-2,-1),(-3,-2),(1,1),(2,1),(3,2)]，红色点是映射到一维空间的数组z。
从上面这个图可以清晰的看到数据的维度明显减少了，数据相关的信息也减少了，这可以很大地减少我们的计算量。
代码如下 （非原创，侵删）：

# !/usr/bin/env python
# !-*-coding:utf-8-*-
# !@Time   : 2019/11/10 12:55
# !@Author : LiQ
# !@File   : PCA.py

# Python实现PCA

import numpy as np
import matplotlib.pyplot as plt


def pca(X, k):  # k is the components you want
    # mean of each feature
    n_samples, n_features = X.shape
    mean = np.array([np.mean(X[:, i]) for i in range(n_features)])
    # normalization
    norm_X = X - mean
    # scatter matrix
    scatter_matrix = np.dot(np.transpose(norm_X), norm_X)
    # Calculate the eigenvectors and eigenvalues
    eig_val, eig_vec = np.linalg.eig(scatter_matrix)
    eig_pairs = [(np.abs(eig_val[i]), eig_vec[:, i]) for i in range(n_features)]
    # sort eig_vec based on eig_val from highest to lowest
    eig_pairs.sort(reverse=True)
    # select the top k eig_vec
    feature = np.array([ele[1] for ele in eig_pairs[:k]])
    # get new data
    data = np.dot(norm_X, np.transpose(feature))
    return data


X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])

x = [-1, -2, -3, 1, 2, 3]
y = [1, -1, -2, 1, 1, 2]

plt.scatter(x, y)
plt.show()

print('结果（一维数据）： \n', pca(X, 1))

三、LDA

（1）概念

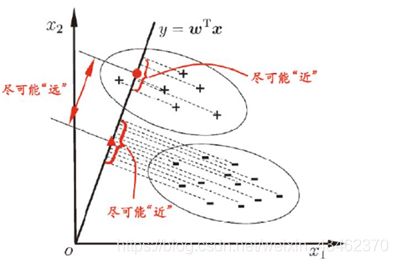
LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。什么意思呢？ 我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。

用下图比较好理解。假设我们有两类数据，分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

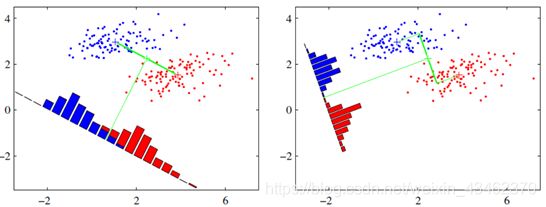
上图中提供了两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好，因为右图的黑色数据和蓝色数据各个较为集中，且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了，当然在实际应用中，我们的数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。

（2）主成分分析（PCA）与线性判别分析（LDA）

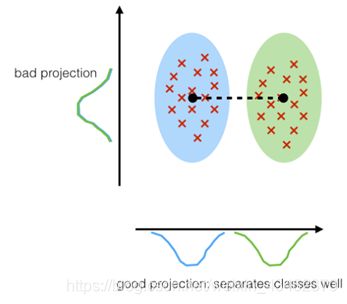
线性判别分析（LDA）和主成分分析（PCA）都是线性变换技术，通常用于降维。PCA可以描述为“无监督”算法，因为它“忽略”类标签，并且其目标是找到使数据集中的方差最大化的方向（所谓的主成分）。与PCA相比，LDA是“受监督的”，并计算方向（“线性判别式”），该方向将表示最大化多个类之间的距离的轴。

对于已知类别标签的多类别分类任务而言，LDA优于PCA，但并非总是如此。例如，使用PCA或LDA后图像识别的分类精度之间的比较表明，如果每个类别的样本数量相对较少，PCA往往会胜过LDA。

实际上，结合使用LDA和PCA也很常见：例如，先使用PCA降低尺寸，然后再使用LDA分类。

（3）如何选择LDA的子空间

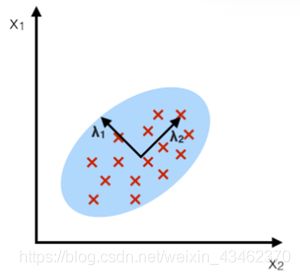
从数据集中计算特征向量（分量），并将它们集中在散点矩阵（即，类间散点矩阵和类内散点矩阵）中。这些特征向量中的每一个都与一个特征值关联，该特征值告诉我们特征向量的“长度”或“幅度”。如果我们观察到所有特征值都具有相似的大小，则这可能是表明我们的数据已经投影在“良好”特征空间上的良好指示。

在另一种情况下，如果某些特征值比其他特征值大得多，我们可以只保留那些特征值最高的特征向量，因为它们包含有关我们数据分布的更多信息。反之亦然，接近0的特征值的信息量较小，我们可以考虑删除那些用于构建新特征子空间的特征值。

（4）计算LDA的5个步骤

1 计算数据集中不同类别的dd维平均向量。

2 计算散点矩阵（类间和类内散点矩阵）。

3 计算这些散点矩阵的特征值和相应的特征向量。

4 通过减少特征值对特征向量进行排序，并选择特征值最大的k个特征向量以形成d×k维的矩阵W（其中每一列代表一个特征向量）。

5 使用此d×k特征向量矩阵将样本转换到新的子空间上。这可以通过矩阵乘法来计算：Y= X×W（其中X是代表n个样本的n×d维矩阵，而Y是变换到新的子空间的n×k维样本矩阵。

（5）LDA实验

X = [17.45004527 15.36597257;17.16106096 17.23406055;18.9139438  19.62288181;18.20160754 18.53543916;17.13266221 15.14689766;18.0411291  17.61342106;19.81482771 18.0051929 ;18.88691647 16.81822867;4.53332949  3.75310005;2.91893428  3.53539434;2.78410779  6.20185479;6.55672681  6.47070796;2.74839608  3.73922573;3.63788487  6.2671882 ;5.95220962  6.53634584;3.78386286  6.37823636;];
W = [0.83317674,0.55300679]';

这里X是用高斯分布随机生成二维两类数组，均值都为5，方差分别是15和2。经过LDA计算后的特征向量是W，用W乘上原数组后得到降维后的数组Y，如下图所示。其中蓝色点是X的分布，红色点是降维后的结果Y的分布。

代码如下：

# !/usr/bin/env python
# !-*-coding:utf-8-*-
# !@Time   : 2019/11/10 13:00
# !@Author : LiQ
# !@File   : LDA.py

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import xlwt


# 计算均值,要求输入数据为numpy的矩阵格式，行表示样本数，列表示特征
def meanX(data):
    return np.mean(data, axis=0)  # axis=0表示按照列来求均值，如果输入list,则axis=1


# 计算类内离散度矩阵子项si


def compute_si(xi):
    n = xi.shape[0]
    ui = meanX(xi)
    si = 0
    for i in range(0, n):
        si = si + (xi[i, :] - ui).T * (xi[i, :] - ui)
    return si


# 计算类间离散度矩阵Sb
def compute_Sb(x1, x2):
    dataX = np.vstack((x1, x2))  # 合并样本
    print("dataX:", dataX)
    # 计算均值
    u1 = meanX(x1)
    u2 = meanX(x2)
    u = meanX(dataX)  # 所有样本的均值
    Sb = (u - u1).T * (u - u1) + (u - u2).T * (u - u2)
    return Sb


def LDA(x1, x2):
    # 计算类内离散度矩阵Sw
    s1 = compute_si(x1)
    s2 = compute_si(x2)
    # Sw=(n1*s1+n2*s2)/(n1+n2)
    Sw = s1 + s2

    # 计算类间离散度矩阵Sb
    # Sb=(n1*(m-m1).T*(m-m1)+n2*(m-m2).T*(m-m2))/(n1+n2)
    Sb = compute_Sb(x1, x2)

    # 求最大特征值对应的特征向量
    eig_value, vec = np.linalg.eig(np.mat(Sw).I * Sb)  # 特征值和特征向量
    index_vec = np.argsort(-eig_value)  # 对eig_value从大到小排序，返回索引
    eig_index = index_vec[:1]  # 取出最大的特征值的索引
    w = vec[:, eig_index]  # 取出最大的特征值对应的特征向量
    return w


def createDataSet():
    X1 = np.mat(np.random.random((8, 2)) * 5 + 15)  #类别A
    X2 = np.mat(np.random.random((8, 2)) * 5 + 2)   #类别B
    return X1, X2


def save_excel(tag_name, file_name):
    workbook = xlwt.Workbook(encoding='utf-8')
    booksheet = workbook.add_sheet('Sheet 1', cell_overwrite_ok=True)
    for i, row in enumerate(tag_name):
        for j, col in enumerate(row):
            booksheet.write(i, j, col)
    workbook.save('%s.xls' % file_name)


x1, x2 = createDataSet()
x = [x1, x2]
print('产生的数据 X 是： \n', x)
# save_excel(x, x)

w = LDA(x1, x2)
print("特征向量w: \n", w)
# save_excel(w, w)

# 编写一个绘图函数
def plotFig(group):
    fig = plt.figure()
    plt.ylim(0, 30)
    plt.xlim(0, 30)
    ax = fig.add_subplot(111)
    ax.scatter(group[0, :].tolist(), group[1, :].tolist())
    plt.show()


# 绘制图形
plotFig(np.hstack((x1.T, x2.T)))

test2 = np.mat([2, 8])
g = np.dot(w.T, test2.T - 0.5 * (meanX(x1)-meanX(x2)).T)
print("Output: ", g)

和前面图2 PCA例子得到的图像比较可以看出，经LDA计算后得到的图像中，两类数据在降维后明显分离的很远，这也突出了LDA的特点是：让类间距离变大，让类内距离变小。

四、SVM（支持向量机）

以下引用自某位博主的文章，侵删

SVM本身就是一个二值分类器，最初是为二分类问题设计，就是回答Yes/No。

**示例：**桌面上有两种颜色混乱的小球，我们将这两种小球区分开，我们猛拍桌面小球会腾起，在腾空的一刹那，会出现一个水平切面，将这两种颜色区分开。

**原因：**二维平面无法找出一条直线来区分小球颜色，但是在三维空间，我们可以找到一个平面来区分小球，该平面叫做超平面。

SVM计算过程就是帮我们找到一个超平面的过程，该超平面就是SVM分类器。

一个简单的二分类问题如下图：

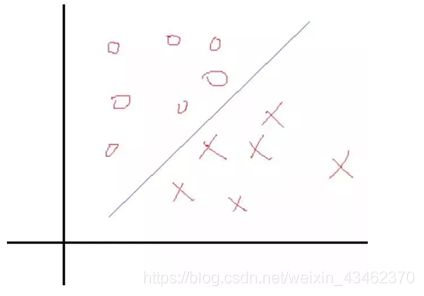
我们希望找到一个决策面使得两类分开，这个决策面一般表示就是WTX+b=0,现在的问题是找到对应的W和b使得分割最好，这个问题实际上就是找一个权值。

假设我们知道了结果，就是上面这样的分类线对应的权值W和b。那么我们会看到，在这两个类里面，是不是总能找到离这个线最近的点，像下面这样：

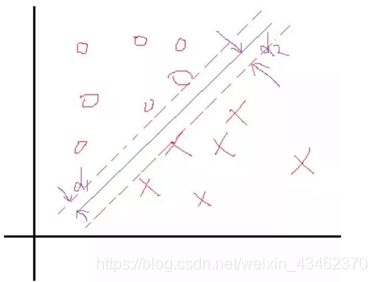
五、基于PCA图像重建和LDA的人脸识别

识别的主要步骤如下：
第1步：预处理数据库中的所有图像，主要包括直方图均衡化，几何标准化，图像平滑化，并可能去除照明，阴影，照明效果；

第2步：从人脸数据库中随机分为训练集，其余为测试集；

第3步：使用内部类协方差矩阵Si = E {（A-μi）（A-μi）T |A∈ωi}作为生成矩阵，然后获得所有单个特征子空间Wi，i = 1,2,3…m。首先，计算生成矩阵Si的特征值和对应的特征向量，其次，将这些特征值按从大到小的顺序排列，类似地，将对应的特征向量从大到小的顺序排列，其次，选择其中的一些特征值生成结构化特征子空间，然后获得所有40类面部图像Wi，i = 1,2,3,40的特征子空间;

第4步：从原始图像Xj中减去重建图像Yij，得到残差图像X，X = Xj-Yij；

第5步：在残差图像中执行LDA，通过等式计算LDA基本图像Wlda和系数矩阵；

第6步：将测试集映射到特征子空间，类似地重复步骤4–6以提取测试集特征；

第7步：利用训练仪的功能训练SVM，并利用测试仪的功能和SVM识别人脸图像。

这部分源代码转自这位博主，写的非常好：东城青年

（1）显示主成分人脸

function visualize(V)  
%显示主成分脸（变换空间中的投影向量，即单位特征向量），这里显示前20个主成分脸，即将原始数据降至20维
figure  
img=zeros(112,92);  
for i=1:20  
    img(:)=V(:,i);  
    subplot(4,5,i);  
    imshow(img,[])  
end

下图是基于ORL人脸库显示的主成分人脸。这是经过快速PCA算法后得到的，显示主成分脸（变换空间中的投影向量，即单位特征向量），这里显示前20个主成分脸，即将原始数据降至20维。

（2）基于主成分分量的人脸重建

%k为重建至多少维
function rebuid(y,k)
 
%导入平均矩阵meanVec和主成分向量V
load ORL/PCA.mat
 
temp = meanVec;
for i = 1:k    
    xi = (y - meanVec) * V(:,i);%某人脸y在第i维的投影值
    yi =  xi * V(:,i)';%某人脸y在第i维的向量值
    temp = temp + yi ;%对该人脸投影到所有维的向量进行一个矢量相加，得到该人脸向量的一个近似值
end
%显示重建人脸
I = zeros(112,92);
I(:) = temp';
imshow(I,[]);

下图对某人脸图像进行主成分分量的重建，分别基于前10，50，100，150维重建后的人脸如下，可见原来的10304维人脸用150维左右就可重建出来：

目前还有一个实时人脸识别没有做出来（主要是模型因为 MinGW64 编译器下载不了，没有跑出来）。