降维-线性判别分析（LDA）

线性判别分析(Linear Discriminant Analysis, LDA)，也叫 做Fisher线性判别(Fisher Linear Discriminant ,FLD)，是模式识别的经典算法，1936年由Ronald Fisher首次提出，并在1996年由Belhumeur引入模式识别和人工智能领域。

一、基本思想

线性判别分析的基本思想是将高维的模式样本投影到最佳低维鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果。 投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。因此，它是一种有效的特征抽取方法。使用这种方法能够使投 影后模式样本的类间散布矩阵最大，并且同时类内散布矩阵最小。

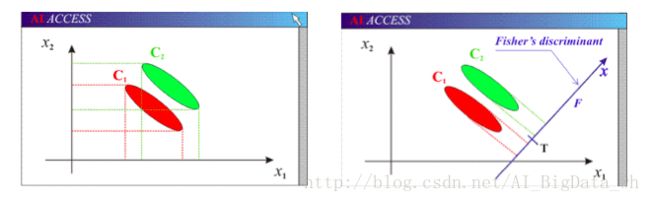
可以看到两个类别，一个绿色类别，一个红色类别。左图是两个类别的原始数据，现在要求将数据从二维降维到一维。直接投影到 x1 轴或者 x2 轴，不同类别之间会有重复，导致分类效果下降。右图映射到的直线就是用LDA方法计算得到的，可以看到，红色类别和绿色类别在映射之后之间的距离是最大的，而且每个类别内部点的离散程度是最小的（或者说聚集程度是最大的）。

二、LDA vs PCA

LDA与PCA(主成分分析)都是常用的降维技术。PCA主要是从特征的协方差角度，去找到比较好的投影方式。LDA更多的是考虑了标注，即希望投影后不同类别之间数据点的距离更大，同一类别的数据点更紧凑。

三、LDA算法具体推导

要说明白LDA，首先得弄明白线性分类器(Linear Classifier)：因为LDA是一种线性分类器。对于K-分类的一个分类问题，会有K个线性函数：

yk(x)=wTkx+wk0.

当满足条件：对于所有的 j ，都有 yk>yj 的时候，我们就说 x 属于类别 k 。对于每一个分类，都有一个公式去算一个分值，在所有的公式得到的分值中，找一个最大的，就是所属的分类。

仔细研究一下上式，就会发现上式实际上就是一种投影，是将一个高维的点投影到一条高维的直线上。LDA最求的目标是，给出一个标注了类别的数据集，投影到了一条直线之后，能够使得点尽量的按类别区分开，当 k=2 即二分类问题的时候，如下图所示：

黄色的五角形点为0类的原始点、蓝色的圆形点为1类的原始点，经过原点的那条红线就是投影的直线。从图上可以清楚的看到，经过LDA降维处理，黄色的点和蓝色的点被原点明显的分开了。

下面我来推导一下二分类LDA问题的公式。为简化起见，假设用来区分二分类的直线(投影函数)为：

y=wTx.

LDA分类的一个目标是使得不同类别之间的距离越远越好， 同一类别之中的距离越近越好，所以我们需要定义几个关键的值：

• 类别 i 的原始中心点(均值)为( Di 表示属于类别 i 的点集合， |Di|=ni ): mi=1ni∑x∈Dix ;
• 类别 i 投影后的中心点为： m¯i=wTmi ;
• 衡量类别 i 投影后，类别点之间的分散程度(方差)为： s¯i=∑y∈Yi(y−m¯i) ;
• 最终我们可以得到一个下面的公式，表示LDA投影到 w 后的目标优化函数：
  
  J(w)=|m¯1−m¯2|2s¯1+s¯2.
  
  分母表示每一个类别内的方差之和，方差越大表示一个类别内的点越分散，分子为两个类别各自的中心点的距离的平方，我们最大化 J(w) 就可以求出最优的 w 。

四、LDA优化问题求解

定义一个投影前的各类别分散程度的矩阵 Si ，这个矩阵看起来有一点麻烦，其实意思是：如果某一个分类的输入点集 Di 里面的点距离这个分类的中心点 mi 越近，则 Si 里面元素的值就越小，如果分类的点都紧紧地围绕着 mi ，则 Si 里面的元素值越更接近0：

Si=∑x∈Di(x−mi)(x−mi)T,

带入 Si ，将 J(w) 分母化为：

s¯i=∑x∈Di(wTx−wTmi)2=∑x∈DiwT(x−mi)(x−mi)Tw=wTSiw,

s¯1+s¯2=wT(S1+S2)w=wTSww

同样的将 J(w) 分子化为：

|m¯1−m¯2|2=wT(m1−m2)(m1−m2)Tw=wTSBw.

这样目标优化函数可以化成下面的形式：

J(w)=wTSBwwTSww.

注意分子分母都是关于 w 的二次项，因此 maxJ(w) 的解与 w 的长度无关，只与其方向有关（如将 w 扩大 k 倍，分子分母同时扩大 k2 倍，可直接约掉）。不是一般性，令 wTSww=1 ，则无约束优化问题 maxJ(w) 变成如下有约束优化问题：

minw−wTSBw,st.wTSww=1

由拉格朗日乘子法，上式等价于

SBw=λSww.

注意到 SBw 的方向恒为 m1−m2 ，不妨令

SBw=λ(m1−m2).

则可得

λ(m1−m2)=λSww.

因此求得 w 为

w=S−1w(m1−m2).

对于 c(c>2) 分类的问题，假定样本数目为 N ，每个类别的样本数 ni ，就可以直接写出以下的结论：

Sw=∑i=1cSi,SB=∑i=1cni(mi−m)(mi−m)T,m=1N∑∀xx,SBwi=λSwwi

若将问题向量化，求解问题变成： SBW=λSwW 。这同样是一个求特征值的问题，求出的第 i 大的特征向量，即为对应的 wi 。

五、LDA算法实战（R语言）

data(iris) 
attach(iris) 
summary(iris) 
library(MASS) 
irislad<-lda(iris[,c(1:4)],Species) 
predict(irislad) 
predict(irislad)$x #lists the linear discriminent scores for each sample 
predict(irislad)$posterior #lists the probabilities that a sample belongs to a specific classification grouo 
predict(irislad)$class #shows the classification group 
table(iris$Species,predict(irislad)$class) 
chisq.test(iris$Species,predict(irislad)$class) 
##plot the Untrained Data(n=150) by LDA coordinates 
plot(predict(irislad)$x,type="n",xlab="LD I",ylab="LD II",main=" Untrained Iris LDA(n=150)") 
text(predict(irislad)$x,levels(predict(irislad)$class)[predict(irislad)$class],col=unclass(iris$Species),cex=1.5) 
abline(h=0);abline(v=0)