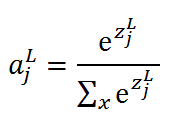机器学习(11.5)--神经网络(nn)算法的深入与优化(5) -- softmax的代码实现
在前面的 TensorFlow实例(4)--MNIST简介及手写数字分类算法 中用到 TensorFlow自带了一个softmax的激活函数
同时 机器学习(11.2)--神经网络(nn)算法的深入与优化(2) -- QuadraticCost、CorssEntropyCost、SoftMax的javascript数据演示测试代码
可以下载一个HTML 里面有一个SoftMax的javascript数据演示测试小程序
那Softmax 到底是什么,有什么用呢?
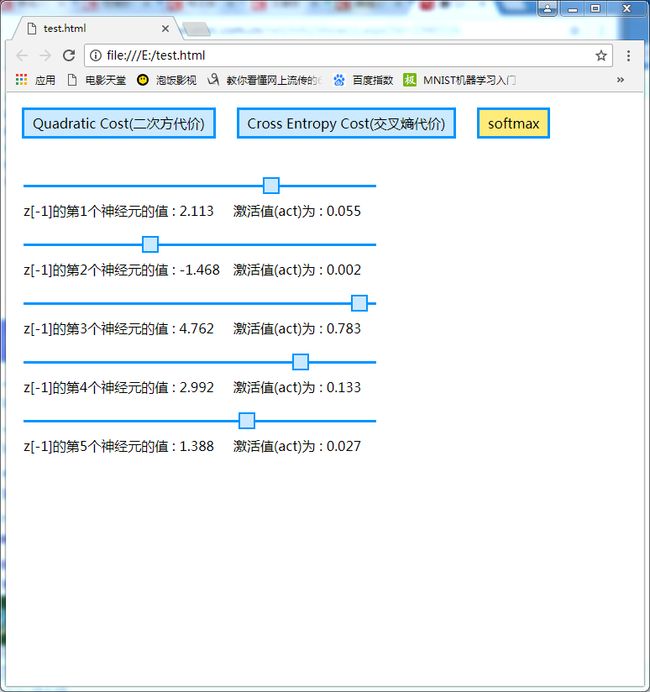
如果你下载了前在的小程序,在某个拉动滑块时你会发现
对应的神经元的值发生改变,同时,所有的激活值会一同发生变化,
如再仔细观察,你会发现 所有激活值的和等1
这样做有什么用?这 对结果的正确性一点用处都没有,它的 用处在于让结果可描述
如我们前面的minst的结果y是一个10个神经元,我们使用sigmoid做为激活函数,计算的值有大有小,我们只能取出最大值做为我们的结果,但每个值代表什么却没办法描述出来
但如果把最后一层的激活函数改成Softmax的算法,这时,这10个神经元的值,总和必然为1
那么我们就可以用语言来描述这个结果,设结果是[0.01,0.02,0.9,0.005...]
描述的方式就是 这张图片是2的概率是90%,0的概率是1%,1的概率是2%,3的概率是0.5%。
在公式中L表示第L层神经元,j表示在L层上第J个神经元,如果要证明所有值的和必为1也很容易
后面的一句就是大写的尴尬了,我只知道最后求偏导得到的 b[-1]=delta= a[-1] - y ,和CorssEntropyCost做为代价函数的偏导结果是一样的
但这个求偏导的求解过程不太清楚,不好意思,如果有会的朋友也告诉我一下呢
因为我们只对最后一层求softmax 所以只要 CorssEntropyCost 在正向计算的后面重新计算a[-1]即可
同时 机器学习(11.2)--神经网络(nn)算法的深入与优化(2) -- QuadraticCost、CorssEntropyCost、SoftMax的javascript数据演示测试代码
可以下载一个HTML 里面有一个SoftMax的javascript数据演示测试小程序

那Softmax 到底是什么,有什么用呢?
如果你下载了前在的小程序,在某个拉动滑块时你会发现
对应的神经元的值发生改变,同时,所有的激活值会一同发生变化,
如再仔细观察,你会发现 所有激活值的和等1
这样做有什么用?这 对结果的正确性一点用处都没有,它的 用处在于让结果可描述
如我们前面的minst的结果y是一个10个神经元,我们使用sigmoid做为激活函数,计算的值有大有小,我们只能取出最大值做为我们的结果,但每个值代表什么却没办法描述出来
但如果把最后一层的激活函数改成Softmax的算法,这时,这10个神经元的值,总和必然为1
那么我们就可以用语言来描述这个结果,设结果是[0.01,0.02,0.9,0.005...]
描述的方式就是 这张图片是2的概率是90%,0的概率是1%,1的概率是2%,3的概率是0.5%。
Softmax的算法 :
我们最终目的是要得到一个概率,所以中间层用softmax没有任何意义,只对最后一层使用即可,同时训练的过程意义也不太大在公式中L表示第L层神经元,j表示在L层上第J个神经元,如果要证明所有值的和必为1也很容易
后面的一句就是大写的尴尬了,我只知道最后求偏导得到的 b[-1]=delta= a[-1] - y ,和CorssEntropyCost做为代价函数的偏导结果是一样的
但这个求偏导的求解过程不太清楚,不好意思,如果有会的朋友也告诉我一下呢
因为我们只对最后一层求softmax 所以只要 CorssEntropyCost 在正向计算的后面重新计算a[-1]即可
以下这小段是在训练过程增加的内容,其实从softmax的作用来看,在训练过程加这个也意义不大,不加也没有什么影响
for w,b in zip(weights,biases):
z = np.dot(w,acts[-1]) + b
zs.append(z)
acts.append(sigmoid(z))
#在正向计算的后面重新计算a[-1]即可
sumExp=np.exp(zs[-1]).sum()
for index in range(len(acts[-1])):
acts[-1][index]=np.exp(zs[-1][index])/sumExp以下这小段是在测试过程增加与调整的内容,
def predict(test_data,weights,biases):
#6、正向计算测试集:计算出结果
#7、和正确结果比较,统计出正确率
correctNum=0
for testImg,testLabel in test_data:
for index,value in enumerate(zip( weights,biases)):
w=value[0]
b=value[1]
if index最后附上所有代码
# -*- coding:utf-8 -*-
import pickle
import gzip
import numpy as np
import random
#激活函数
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
def sigmoid_deriv(z):
return sigmoid(z) * (1 - sigmoid(z))
#读取数据
def loadData(trainingNum = None,testNum=None):
with gzip.open(r'mnist.pkl.gz', 'rb') as f:
training_data, validation_data, test_data = pickle.load(f,encoding='bytes')
training_label = np.zeros([training_data[1].shape[0],10,1])
for index,val in enumerate(training_data[1]): training_label[index][val] = 1
training_data = list(zip(training_data[0].reshape(-1,784,1),training_label))
test_data = list(zip(test_data[0].reshape(-1,784,1),test_data[1]))
if trainingNum !=None:
training_data = training_data[0:trainingNum]
if trainingNum !=None:
test_data = test_data[0:testNum]
return training_data,test_data
def batchData(batch,layers,weights,biases):
batch_w = [np.zeros(b.shape) for b in weights]
batch_b = [np.zeros(b.shape) for b in biases]
for item in batch:
item_w,item_b=itemData(item,layers,weights,biases)
#当batch下每条记录计算完后加总
for index in range(0,len(batch_w)):
batch_w[index] = batch_w[index] + item_w[index]
batch_b[index] = batch_b[index] + item_b[index]
return batch_w,batch_b
def itemData(item,layers,weights,biases):
'''单条记录的正反向计算'''
#正向计算
zs = []
acts = [item[0]]
for w,b in zip(weights,biases):
z = np.dot(w,acts[-1]) + b
zs.append(z)
acts.append(sigmoid(z))
#在正向计算的后面重新计算a[-1]即可
sumExp=np.exp(zs[-1]).sum()
for index in range(len(acts[-1])):
acts[-1][index]=np.exp(zs[-1][index])/sumExp
#反向计算
item_w = [np.zeros(b.shape) for b in weights]
item_b = [np.zeros(b.shape) for b in biases]
for index in range(-1,-1 * len(layers),-1):
if index == -1:
item_b[index] = acts[index] - item[1]
else:
item_b[index] = np.dot(weights[index + 1].T,item_b[index + 1])
#二次方代价函数 两个差别只是后面有没有乘 * sigmoid_deriv(zs[index])
#在代码中的差异只是进位不同,
#item_b[index] = item_b[index] * sigmoid_deriv(zs[index])
item_b[index] = item_b[index] * sigmoid_deriv(zs[index]) #交叉熵代价函数
item_w[index] = np.dot(item_b[index],acts[index - 1].T)
return item_w,item_b
def predict(test_data,weights,biases):
#6、正向计算测试集:计算出结果
#7、和正确结果比较,统计出正确率
correctNum=0
for testImg,testLabel in test_data:
for index,value in enumerate(zip( weights,biases)):
w=value[0]
b=value[1]
if index