LeetCode 第22场双周赛

1、给你两个整数数组 arr1 ， arr2 和一个整数 d ，请你返回两个数组之间的 距离值 。距离值：定义为符合此描述的元素数目：对于元素 arr1[i] ，不存在任何元素 arr2[j] 满足 |arr1[i]-arr2[j]| <= d 。
链接: https://leetcode-cn.com/problems/find-the-distance-value-between-two-arrays/
示例 1：

输入：arr1 = [4,5,8], arr2 = [10,9,1,8], d = 2
输出：2
解释：
对于 arr1[0]=4 我们有：
|4-10|=6 > d=2
|4-9|=5 > d=2
|4-1|=3 > d=2
|4-8|=4 > d=2
对于 arr1[1]=5 我们有：
|5-10|=5 > d=2
|5-9|=4 > d=2
|5-1|=4 > d=2
|5-8|=3 > d=2
对于 arr1[2]=8 我们有：
|8-10|=2 <= d=2
|8-9|=1 <= d=2
|8-1|=7 > d=2
|8-8|=0 <= d=2

class Solution:
    def findTheDistanceValue(self, arr1: List[int], arr2: List[int], d: int) -> int:
        res = 0
        for a in arr1:
            if all(abs(a - b) > d for b in arr2):
                res += 1
        return res

2、

如上图所示，电影院的观影厅中有 n 行座位，行编号从 1 到 n ，且每一行内总共有 10 个座位，列编号从 1 到 10 。给你数组 reservedSeats ，包含所有已经被预约了的座位。比如说，researvedSeats[i]=[3,8] ，它表示第 3 行第 8 个座位被预约了。
请你返回 最多能安排多少个 4 人家庭 。4 人家庭要占据 同一行内连续 的 4 个座位。隔着过道的座位（比方说 [3,3] 和 [3,4]）不是连续的座位，但是如果你可以将 4 人家庭拆成过道两边各坐 2 人，这样子是允许的。
示例 1：
输入：n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
输出：4
解释：上图所示是最优的安排方案，总共可以安排 4 个家庭。蓝色的叉表示被预约的座位，橙色的连续座位表示一个 4 人家庭。

class Solution:
    def maxNumberOfFamilies(self, n: int, re: List[List[int]]) -> int:
        rows = collections.defaultdict(set)
        
        for i, j in re:
            rows[i].add(j)
        
        res = (n - len(rows)) * 2
        for r in rows:
            flag = True
            if all(j not in rows[r] for j in [2, 3, 4, 5]):
                flag = False
                res += 1
            if all(j not in rows[r] for j in [6, 7, 8, 9]):
                flag = False
                res += 1
            if flag:
                if all(j not in rows[r] for j in [4, 5, 6, 7]):
                    res += 1
        return res

3、我们将整数 x 的 权重 定义为按照下述规则将 x 变成 1 所需要的步数：
1）如果 x 是偶数，那么 x = x / 2
2）如果 x 是奇数，那么 x = 3 * x + 1。比方说，x=3 的权重为 7 。因为 3 需要 7 步变成 1 （3 --> 10 --> 5 --> 16 --> 8 --> 4 --> 2 --> 1）。
给你三个整数 lo， hi 和 k 。你的任务是将区间 [lo, hi] 之间的整数按照它们的权重升序排序 ，如果大于等于 2 个整数有 相同 的权重，那么按照数字自身的数值 升序排序 。请你返回区间 [lo, hi] 之间的整数按权重排序后的第 k 个数。
示例 1：
输入：lo = 12, hi = 15, k = 2
输出：13
解释：12 的权重为 9（12 --> 6 --> 3 --> 10 --> 5 --> 16 --> 8 --> 4 --> 2 --> 1）
13 的权重为 9
14 的权重为 17
15 的权重为 17
区间内的数按权重排序以后的结果为 [12,13,14,15] 。对于 k = 2 ，答案是第二个整数也就是 13 。注意，12 和 13 有相同的权重，所以我们按照它们本身升序排序。14 和 15 同理。

class Solution:
    def getKth(self, lo: int, hi: int, k: int) -> int:
        arr = list(range(lo, hi + 1))
        
        import functools
        @functools.lru_cache(None)
        def f(i):
            if i == 1:
                return 0, i
            if i % 2 == 0:
                return f(i // 2)[0] + 1, i
            return f(3 * i + 1)[0] + 1, i
        
        arr.sort(key=lambda i:f(i))        
        return arr[k - 1]

4、给你一个披萨，它由 3n 块不同大小的部分组成，现在你和你的朋友们需要按照如下规则来分披萨：
1）你挑选 任意 一块披萨。
2）Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
3）Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
重复上述过程直到没有披萨剩下。每一块披萨的大小按顺时针方向由循环数组 slices 表示。请你返回你可以获得的披萨大小总和的最大值。
示例 1：

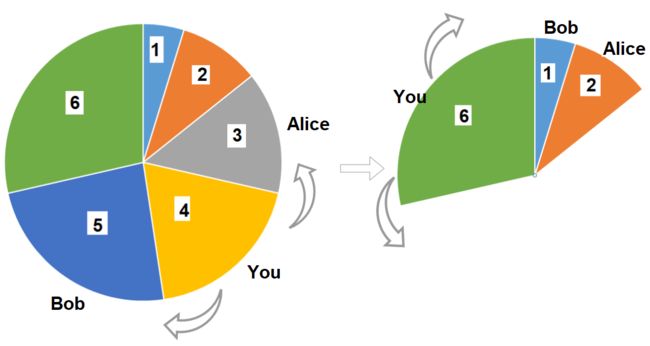
输入：slices = [1,2,3,4,5,6]
输出：10
解释：选择大小为 4 的披萨，Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨，Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。

class Solution:
    def maxSizeSlices(self, slices: List[int]) -> int:
        import functools
        @functools.lru_cache(None)
        def dp(i, j, k, loop = 0):
            if k == 1:
                return max(slices[i:j+1])
            if j - i + 1 < k * 2 - 1:
                return -float('inf')
            return max(dp(i + loop, j - 2, k - 1) + slices[j], dp(i, j - 1, k))
        
        return dp(0, len(slices) - 1, len(slices) // 3, 1)