CS231n -- assigment2 FullyConnectedNet \ BN \ Dropout
都大三下了,课业还是很重,被光纤光学虐了两天,今天终于可以继续开始撸CS231n啦\^o^/.
这次是Fully-connected Nerual Network + Batch Normalization + Dropout.
Part 1 Fully-connected Nerual Network
在assignment1中,我们已经完成了一个两层的全连接层,实现比较简单但模块化不够好。现在我们要做的是使用更模块化的设计来构建网络,这样我们就可以分别构建不同层数,然后将它们组合成不同结构的模型。
在这个作业中,我们要使用更模块化的方法来实现全连接网络。对于每一层,我们要实现一个forward和backward。
前向传播函数接受input、weight和其他参数,返回output和cache,用于存储反向传播时需要的数据。
反向传播接收upstream传下来的偏导和cache缓存,返回关于input和weights的梯度。
好,最先看fc_net.py,一开始要完成class TwoLayerNet,emmm,跟上次作业完全一样,迅速完成。然后是FullyConnectedNet类,基本思路与两层的相同,通过循环来进行参数的初始化,这里贴上一小段实现过程,其余部分套用这种方式即可。 PS:如果使用batch normalization,直接中间插入gamma与beta就行。
for i in range(len(hidden_dims)):
layer = hidden_dims[i]
self.params['W'+str(i+1)] = np.random.normal(0, weight_scale, size=(input_dim, layer))
self.params['b'+str(i+1)] = np.zeros(layer)
if self.use_batchnorm:
self.params['gamma'+str(i+1)] = np.ones(layer)
self.params['beta'+str(i+1)] = np.zeros(layer)
input_dim = layer
self.params['W'+str(self.num_layers)] = np.random.normal(0, weight_scale, size=(layer, num_classes))
self.params['b'+str(self.num_layers)] = np.zeros(num_classes)对于较少的数据,细心点调一调参,20个epoch可以过拟合。
这个思考题大家都可以看看:
还需要完成的是几种优化方法,根据cs231n -- better optimization的公式,直接写就行
sgd_momentum
mu是超参数,多用0.9,交叉验证可用[0.5, 0.9, 0.95, 0.95]
mu=config['momentum']
learning_rate=config['learning_rate']
v = mu* v - learning_rate * dw # integrate velocity
next_w = w+vrmsprop
decay_rate是超参,多用[0.9, 0.99, 0.999];eps范围1e-4~1e-8
decay_rate=config['decay_rate']
cache=config['cache']
learning_rate = config['learning_rate']
eps=config['epsilon']
cache = decay_rate * cache + (1 - decay_rate) * dx ** 2
next_x =x- learning_rate * dx / (np.sqrt(cache) + eps)adam
推荐超参数eps = 1e-8,beta1 = 0.9, beta2 = 0.999
learning_rate = config['learning_rate']
m=config['m']
beta1=config['beta1']
beta2 = config['beta2']
v=config['v']
eps = config['epsilon']
t=config['t']
t+=1
m = beta1 * m + (1 - beta1) * dx
mt = m / (1 - beta1 ** t)
v = beta2 * v + (1 - beta2) * (dx ** 2)
vt = v / (1 - beta2 ** t)
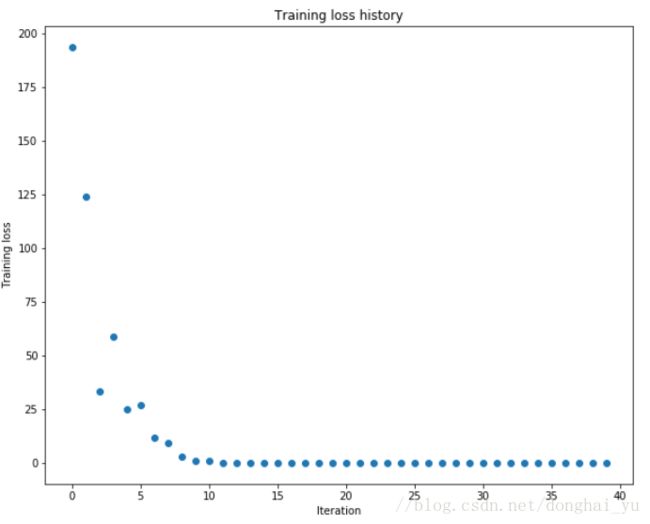
next_x =x - learning_rate * mt / (np.sqrt(vt) + eps)附上实际使用几种优化方法的效果
sgd效果最差,收敛速度最慢;momentum与rmsprop看起来效果差不多;相对而言adam表现最好。
当然,看这可怜的结果,接下来一番调参又是跑不了。我大概调了调,满足了作业50%正确率要求,就没继续花时间在上面了(CNN有更好的效果,有空仔细做CNN去),以下参数给大家参考下:
solver = Solver(model, data, print_every=500, batch_size=100,
update_rule = 'adam',optim_config={'learning_rate':3e-3},
lr_decay=0.85, verbose=True)
solver.train()Part2 Batch Normalization
对于BN的理解和推导是好些天前了,先复习下囧rz。cs231n -- Batch Normalization
看到作业的引言,笑着哭,对BN的总结写的真好,忍不住必须搬过来啊(得意)
前向传播(layers.py)
按照公式一个个计算就好,注意尺寸,一定能实现~
train:
batch_mean = np.mean(x, axis = 0)
batch_var = np.var(x, axis = 0)
xhat = (x - batch_mean) / np.sqrt(batch_var + eps)
out = gamma * xhat + beta
cache = (gamma, x, batch_mean, batch_var, eps, xhat)
running_mean = momentum * running_mean + (1 - momentum) * batch_mean
running_var = momentum * running_var + (1 - momentum) * batch_var注意这里的running_mean与running_var不是通过mini-batch的无偏估计量来计算,而是用基于momentum的指数衰减。
test:
a = gamma / np.sqrt(running_var + eps)
out = a * x + beta - a * running_mean反向传播(layers.py)
反向传播就是按公式来写就行了
gamma, x, mean, var, eps, xhat = cache
N = x.shape[0]
a = np.sqrt(var + eps)
dxhat = dout * gamma
dvar = np.sum((x - mean) * dxhat * (-0.5) / a**3, axis=0)
dmean = np.sum(- dxhat / a, axis=0) + dvar * np.sum(-2 * (x - mean), axis=0) / N
dx = dxhat / a + dvar * 2 * (x - mean) / N + dmean / N
dgamma = np.sum(dout * xhat, axis=0)
dbeta = np.sum(dout, axis=0)至于batchnorm_backward_alt,根据hint,发现其实dmean后后面一项为0,其余一样。emmm,似乎用处不大。
然后,在layer_utils.py中,对affine-bn-relu进行一个简单的二次封装,仿照作业的格式自己写了个注释233.
def affine_bn_relu_forward(x, w, b, gamma, beta, bn_param):
"""
Convenience layer that performs as an affine with Batch Normalization followed by RELU
Inputs:
- x: Input to the affine layer
- w, b :Weights for the affine layer
- gamma: Scale paremeter of shape (D,)
- beta: Shift paremeter of shape (D, )
- bn_param: Dictionary with the following keys:
-mode: 'train' or 'test',required
-eps: Constant fot numeric stability
-momentum: Constant for running mean / variance.
-running_mean: Array of shape (D,) giving running mean of features
-running_var: Array of shape(D,) giving running var of features
Return a tuple of:
- out: of shape (N, D)
- cache: object to give to the backward pass
"""
a, fc_cache = affine_forward(x, w, b)
a_bn, bn_cache = batchnorm_forward(a, gamma, beta, bn_param)
out, relu_cache = relu_forward(a_bn)
cache = (fc_cache, bn_cache, relu_cache)
return our, cache
def affine_bn_relu_backward(dout, cache):
"""
Backward pass for the affine-bn-relu convenience layer
"""
fc_cache, bn_cache, relu_cache = cache
da = relu_backward(dout, relu_cache)
dx, dgamma, dbeta = batchnorm_backward(da, bn_cache)
dx, dw, db = affine_backward(dx, fc_cache)
return dx, dw, db, dgamma, dbeta
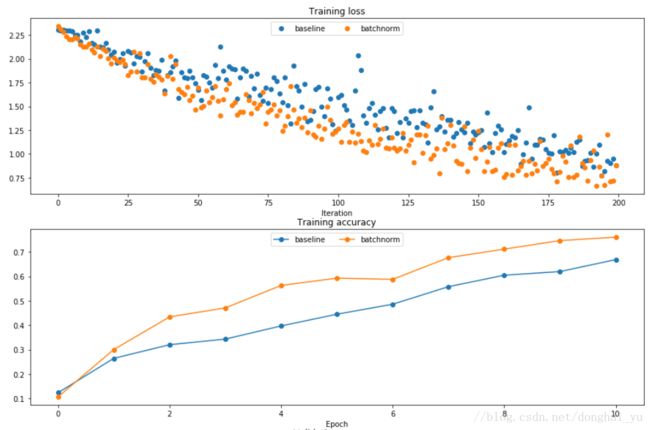
作业中一张效果图,用的同样的学习率,优化方法为Adam,这个主要体现了使用BN后更快的收敛速度。
然后是在不同的Weight_scale下,是否使用BN的情况对比:
以上可以看出两点:
1.使用BN后对于不好的初始化更为鲁棒
2.BN有一定的防止过拟合的作用,在许多初始化情况下,val acc与 train acc之间的gap比不使用BN更小。
符合理论中BN防止梯度爆炸的作用。
Part3 Dropout
dropout是以一定概率选择使用一部分神经元的方式,对于减轻过拟合很有效。
具体来说是:
1.在开始训练的时候随机的(临时)删除一部分神经元,但输入层和输出层不做变动;
2.将输入通过修改后的网络进行前向传播,然后将误差通过修改后的网络进行反向传播;
3.对于另外一批训练样本,重复1,2操作。
对于Dropout的工作机理,我找到了两种解释:
1.用相同的数据训练多个不同的网络可能会得到多个不同的结果,但它们都是对同一个loss function作用,相当于同时对其进行优化,也是在不同方式上过拟合,我们对这些网络的结果取平均可以去掉一些过拟合。
2.减少神经元之间复杂的共适应性。当隐藏层神经元被随机删除后,使得全连接网络具有了一定的稀疏化,从而有效减轻了不同特征的协同效应。也就是说,有些特征可能会依赖与固定关系的隐含节点的共同作用,而通过Dropout的话,就有效组织了某些特征在其他特征存在下才有效果的情况,增加网络的鲁棒性。打个比方:对于一只猫的图像,网络学习到了耳朵、鼻子、尾巴等的特征,使用Dropout后变成了网络1:耳朵+鼻子;网络2:耳朵+尾巴; 网络3:鼻子+尾巴。(CS231n课程中的解释)
实现:
dropout与RELU很类似,我们可以随机生成一个mask来选择神经元,mask中元素为0 1,mask与输入相乘,0使神经元暂时失活,反向也是不参与更新的部分用mask和dout相乘。
#forward#这里借鉴了keras的dropout实现源码
#通过binomial函数,生成与x一样的维数向量。binomial像抛硬币,每个神经元当作一个硬币,
#正面概率为p,n、表示每个神经元实验的次数
#因为每个神经元只需要抛一次,所以n=1,size参数是我们有多少硬币
retain_prop = 1.0 - p
sample = np.random.binomial(n=1, p=retain_prop,size=x.shape)
#将生成一个与x同维度,0、1分布的向量,0表示这个神经元被屏蔽,即dropout了
out = x * sample
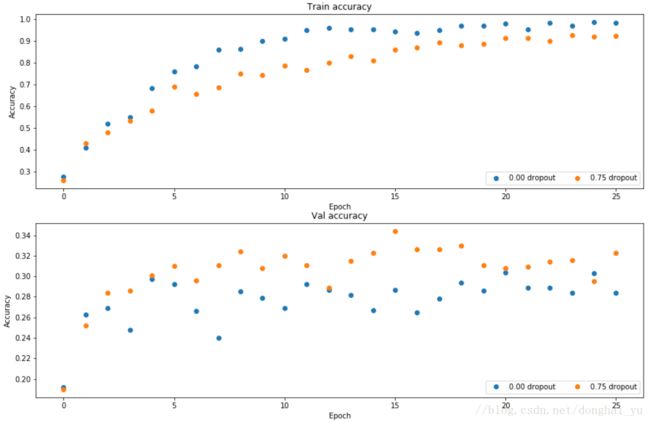
mask = sampledx = dout * mask根据作业给的初始数据,分别用和不用dropout,得到如下结果,使用dropout后train acc 与 val acc的gap明显减小,去过拟合有效果。
接下来要手写CNN了,,真心不是个小任务,还是滚去写固体物理作业吧(逃)。