无监督数据降维技术——线性判别分析

线性判别分析基本原理

线性判别分析（Linear Discriminant Analysis, LDA）是一种可作为特征提取的技术，它可以提高数据分析过程中的计算效率，同时，对于不适用于正则化的模型，它可以降低因维数灾难带来的过拟合。

LDA的基本概念与PCA非常相似，PCA试图在数据集中找到方差最大的正交的主成分分量的轴，而LDA的目标是发现可以最优化分类的特征子空间。LDA与PCA都是可用于降低数据集维度的线性转换技巧。其中，PCA是无监督算法，而LDA是监督算法。与PCA相比，LDA是一种更优越的用于分类的特征提取技术。

下图解释了二类别分类中的LDA概念。类别1、类别2中的样本分别用叉号和圆点来表示：

如上图所示，在 x 轴方向（LD1），通过线性判定，可以很好地将呈现正态分布的两个类分开。虽然沿 y 轴（LD2）方向的线性判定保持了数据集的较大方差，但沿此方向无法提供关于类别区分的任何信息，因此他不是一个好的线性判定。

一个关于LDA的假设就是数据呈正态分布，此外，还假定各类别中数据具有相同的协方差矩阵，且样本的特征从统计上来讲是相互独立的。不过，即使一个或多个假设没有满足，LDA仍旧可以很好地完成降维工作。

计算散布矩阵

分别构建类内散布矩阵和类间散布矩阵。均值向量 mi m i 存储了类别 i 中样本的特征均值 um u m :

葡萄酒数据集的三个类别对应三个均值向量：

import pandas as pd
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.fit_transform(X_test)

import numpy as np
np.set_printoptions(precision=4)
mean_vecs = []
for label in range(1, 4):
    mean_vecs.append(np.mean(X_train_std[y_train == label], axis=0))
    print('MV %s: %s\n' % (label, mean_vecs[label - 1]))

计算结果如下：

MV 1: [ 0.9259 -0.3091  0.2592 -0.7989  0.3039  0.9608  1.0515 -0.6306  0.5354
  0.2209  0.4855  0.798   1.2017]

MV 2: [-0.8727 -0.3854 -0.4437  0.2481 -0.2409 -0.1059  0.0187 -0.0164  0.1095
 -0.8796  0.4392  0.2776 -0.7016]

MV 3: [ 0.1637  0.8929  0.3249  0.5658 -0.01   -0.9499 -1.228   0.7436 -0.7652
  0.979  -1.1698 -1.3007 -0.3912]

通过均值向量，计算类内散布矩阵 SW S W :

累加各类别 i 的散布矩阵 Si S i ：

d = 13 # number of features
S_W = np.zeros((d, d))
for label, mv in zip(range(1, 4), mean_vecs):
    class_scatter = np.zeros((d, d))
    for row in X[y == label]:
        row, mv = row.reshape(d, 1), mv.reshape(d, 1)
        class_scatter += (row - mv).dot((row - mv).T)
    S_W += class_scatter
print('Within-class scatter matrix: %sx%s' % (S_W.shape[0], S_W.shape[1]))

执行结果如下：

Within-class scatter matrix: 13x13

此前对散布矩阵进行计算时，曾假设训练集各类别是均匀分布。但是，通过打印类别的数量，可以看到在此并未遵循此假设：

print('Class label distribution: %s' % (np.bincount(y_train))[1:])

结果如下：

Class label distribution: [40 49 35]

因此，通过累加方式计算散步矩阵 SW S W 前，需要对各类别的散布矩阵 Si S i 做缩放处理。协方差矩阵可以看做是归一化的散布矩阵：

d = 13 # number of features
S_W = np.zeros((d, d))
for label, mv in zip(range(1, 4), mean_vecs):
    class_scatter = np.cov(X_train_std[y_train == label].T)
    S_W += class_scatter
print('Within-class scatter matrix: %sx%s' % (S_W.shape[0], S_W.shape[1]))

执行结果如下：

Within-class scatter matrix: 13x13

在完成类内散布矩阵（或协方差矩阵）的计算后，计算类间散布矩阵 SB S B :

其中，m 为全局均值，它在计算时用到了所有类别中的全部样本。

mean_overall = np.mean(X_train_std, axis=0)
d = 13 # number of features
S_B = np.zeros((d, d))
for i, mean_vec in enumerate(mean_vecs):
    n = X[y == (i + 1), :].shape[0]
    mean_vec = mean_vec.reshape(d, 1)
    mean_overall = mean_overall.reshape(d, 1)
    S_B += n * (mean_vec - mean_overall).dot((mean_vec - mean_overall).T)
print('Between-class scatter matrix: %sx%s' % (S_B.shape[0], S_B.shape[1]))

执行结果如下：

Between-class scatter matrix: 13x13

在新特征子空间上选取线性判别算法

LDA余下的步骤与PCA的步骤相似，只是不对协方差矩阵做特征分解，而且求解矩阵 S−1WSB S W − 1 S B 的广义特征值：

eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
print('Eigenvalues in decreasing order:\n')
for eigen_val in eigen_pairs:
    print(eigen_val[0])

执行结果如下：

Eigenvalues in decreasing order:

643.0153843460513
225.08698185416247
9.858090424938485e-14
8.360518905063732e-14
4.618527782440651e-14
2.878588341817008e-14
2.878588341817008e-14
2.2954665358098825e-14
2.2954665358098825e-14
1.2379202982740725e-14
1.2379202982740725e-14
2.4182588985185695e-15
2.4182588985185695e-15

为了度量线性判别（特征向量）可以获取多少可区分类别的信息，按照特征值降序绘制出对线性判别信息保持程度的图像，在此使用判定类别区分能力的相关信息discriminability。

tot = sum(eigen_vals.real)
discr = [(i / tot) for i in sorted(eigen_vals.real, reverse=True)]
cum_discr = np.cumsum(discr)

import matplotlib.pyplot as plt
plt.bar(range(1, 14), discr, alpha=0.5, align='center', label='individual discriminability')
plt.step(range(1, 14), cum_discr, where='mid', label='cumulative discriminability')
plt.ylabel('discriminability ration')
plt.xlabel('Linear Discriminants')
plt.ylim([-0.1, 1.1])
plt.legend(loc='best')
plt.show()

从结果图像中可以看到，前两个线性判别几乎获取到了葡萄酒训练数据中全部有用信息。

下面叠加前两个判别能力最强的特征向量列来构建转换矩阵W:

W = np.hstack((eigen_pairs[0][1][:, np.newaxis].real, eigen_pairs[1][1][:, np.newaxis].real))
print('Matrix W:\n', W)

执行结果如下：

Matrix W:
 [[-0.0707  0.3778]
 [ 0.0359  0.2223]
 [-0.0263  0.3813]
 [ 0.1875 -0.2955]
 [-0.0033 -0.0143]
 [ 0.2328 -0.0151]
 [-0.7719 -0.2149]
 [-0.0803 -0.0726]
 [ 0.0896 -0.1767]
 [ 0.1815  0.2909]
 [-0.0631 -0.2376]
 [-0.3794 -0.0867]
 [-0.3355  0.586 ]]

将样本映射到新的特征空间

通过乘积方式对训练数据进行转换：

X_train_lda = X_train_std.dot(W)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
    plt.scatter(X_train_lda[y_train == l, 0], X_train_lda[y_train == l, 1] * (-1), c=c, label=l, marker=m)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower right')
plt.show()

使用scikit-learn进行LDA分析

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)
X_train_lda = lda.fit_transform(X_train_std, y_train)

from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
    # setup marker generator and color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[: len(np.unique(y))])

    #plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    #plot class samples
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl)

from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(X_train_lda, y_train)
plot_decision_regions(X_train_lda, y_train, classifier=lr)
plt.ylabel('LD1 ')
plt.xlabel('LD 2')
plt.legend(loc='lower left')
plt.show()

从结果图像中可以看到，逻辑回归模型只误判了类别2中的一个样本。

下面，再来看一下模型在测试数据集上的表现：

X_test_lda = lda.transform(X_test_std)
plot_decision_regions(X_test_lda, y_test, classifier=lr)
plt.ylabel('LD1 ')
plt.xlabel('LD 2')
plt.legend(loc='lower left')
plt.show()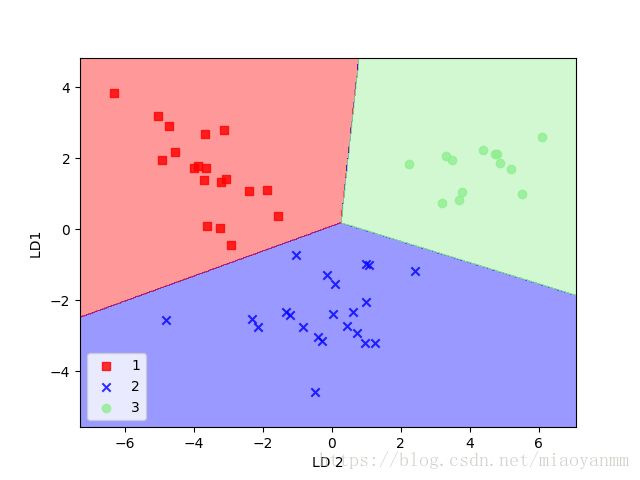

从结果图像中可以看到，当使用只有两维的特征子空间来替代原始数据集中的13个葡萄酒特征时，逻辑回归在测试数据集上对样本的分类结果可谓完美。

参考文献：
Python Machine Learning/Chapter 5: Compressing Data via Dimensionality Reduction