深度学习之手写数字分类
问题描述:
将手写数字的灰度图像(28 像素×28 像素)划分到 10 个类别 中(0~9)。我们将使用 MNIST 数据集,它是机器学习领域的一个经典数据集,其历史几乎和这 个领域一样长,而且已被人们深入研究。这个数据集包含 60 000 张训练图像和 10 000 张测试图 像,由美国国家标准与技术研究院(National Institute of Standards and Technology,即 MNIST 中 的 NIST)在 20 世纪 80 年代收集得到。你可以将“解决”MNIST 问题看作深度学习的“Hello World”,正是用它来验证你的算法是否按预期运行。当你成为机器学习从业者后,会发现 MNIST 一次又一次地出现在科学论文、博客文章等中。
1.准备数据:
import numpy as np
import paddle as paddle
import paddle.fluid as fluid
from PIL import Image
import matplotlib.pyplot as plt
import os
train_reader = paddle.batch(paddle.reader.shuffle(paddle.dataset.mnist.train(),
buf_size=512),batch_size=128)
test_reader = paddle.batch(paddle.dataset.mnist.test(),batch_size=128)
temp_reader = paddle.batch(paddle.dataset.mnist.train(),batch_size=1)
temp_data=next(temp_reader())
print(temp_data)打印以下,观察mnist数据集
G:\RJAZ\python3.6.6\py_data\python.exe I:/PaddlePaddle/code/wrirren_number/main.py
[================================================= ][==================================================]
[==================================================]
[==================================================]
[==================================================]
[(array([-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -0.9764706 , -0.85882354, -0.85882354,
-0.85882354, -0.01176471, 0.06666672, 0.37254906, -0.79607844,
0.30196083, 1. , 0.9372549 , -0.00392157, -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -0.7647059 , -0.7176471 , -0.26274508, 0.20784318,
0.33333337, 0.9843137 , 0.9843137 , 0.9843137 , 0.9843137 ,
0.9843137 , 0.7647059 , 0.34901965, 0.9843137 , 0.8980392 ,
0.5294118 , -0.4980392 , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -0.6156863 , 0.8666667 ,
0.9843137 , 0.9843137 , 0.9843137 , 0.9843137 , 0.9843137 ,
0.9843137 , 0.9843137 , 0.9843137 , 0.96862745, -0.27058822,
-0.35686272, -0.35686272, -0.56078434, -0.69411767, -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -0.85882354, 0.7176471 , 0.9843137 , 0.9843137 ,
0.9843137 , 0.9843137 , 0.9843137 , 0.5529412 , 0.427451 ,
0.9372549 , 0.8901961 , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-0.372549 , 0.22352946, -0.1607843 , 0.9843137 , 0.9843137 ,
0.60784316, -0.9137255 , -1. , -0.6627451 , 0.20784318,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -0.8901961 ,
-0.99215686, 0.20784318, 0.9843137 , -0.29411763, -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , 0.09019613,
0.9843137 , 0.4901961 , -0.9843137 , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -0.9137255 , 0.4901961 , 0.9843137 ,
-0.45098037, -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -0.7254902 , 0.8901961 , 0.7647059 , 0.254902 ,
-0.15294117, -0.99215686, -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-0.36470586, 0.88235295, 0.9843137 , 0.9843137 , -0.06666666,
-0.8039216 , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -0.64705884,
0.45882356, 0.9843137 , 0.9843137 , 0.17647064, -0.7882353 ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -0.8745098 , -0.27058822,
0.9764706 , 0.9843137 , 0.4666667 , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , 0.9529412 , 0.9843137 ,
0.9529412 , -0.4980392 , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -0.6392157 , 0.0196079 ,
0.43529415, 0.9843137 , 0.9843137 , 0.62352943, -0.9843137 ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -0.69411767,
0.16078436, 0.79607844, 0.9843137 , 0.9843137 , 0.9843137 ,
0.9607843 , 0.427451 , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-0.8117647 , -0.10588235, 0.73333335, 0.9843137 , 0.9843137 ,
0.9843137 , 0.9843137 , 0.5764706 , -0.38823527, -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -0.81960785, -0.4823529 , 0.67058825, 0.9843137 ,
0.9843137 , 0.9843137 , 0.9843137 , 0.5529412 , -0.36470586,
-0.9843137 , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -0.85882354, 0.3411765 , 0.7176471 ,
0.9843137 , 0.9843137 , 0.9843137 , 0.9843137 , 0.5294118 ,
-0.372549 , -0.92941177, -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -0.5686275 , 0.34901965,
0.77254903, 0.9843137 , 0.9843137 , 0.9843137 , 0.9843137 ,
0.9137255 , 0.04313731, -0.9137255 , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , 0.06666672, 0.9843137 , 0.9843137 , 0.9843137 ,
0.6627451 , 0.05882359, 0.03529418, -0.8745098 , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. , -1. ,
-1. , -1. , -1. , -1. ], dtype=float32), 5)]2.配置网络
以下的代码判断就是定义一个简单的多层感知器,一共有三层,两个大小为100的隐层和一个大小为10的输出层,因为MNIST数据集是手写0到9的灰度图像,类别有10个,所以最后的输出大小是10。最后输出层的激活函数是Softmax,所以最后的输出层相当于一个分类器。加上一个输入层的话,多层感知器的结构是:输入层-->>隐层-->>隐层-->>输出层。
def multilayer_perceptron(input):
# 第一个全连接层,激活函数为ReLU
hidden1 = fluid.layers.fc(input=input, size=100, act='relu')
# 第二个全连接层,激活函数为ReLU
hidden2 = fluid.layers.fc(input=hidden1, size=100, act = 'relu')
# 以softmax为激活函数的全连接输出层,大小为10
prediction = fluid.layers.fc(input=hidden2, size=10, act = 'softmax')
return prediction定义输入输出层,因为输入的是28*28的灰度图像,所以它的形状是[1,28,28]的,1表示的是颜色通道,如果是彩色图,则应为[3,28,28],因为彩色图有RGB三个通道
image = fluid.layers.data(name = 'image', shape=[1,28,28], dtype='float32')
label = fluid.layers.data(name='label', shape=[1], dtype='int64')获取分类器,,这里用定义好的函数来获取
model = multilayer_perceptron(image)接下来定义损失函数
这里使用的是交叉熵损失函数,此函数在分类上比较常用
cost = fluid.layers.cross_entropy(input=model, label=label)#使用交叉熵损失函数,描述真实样本标签和预测概率之间的差值定义了一个损失函数之后,还有对它求平均值,因为定义的是一个Batch的损失值。
avg_cost = fluid.layers.mean(cost)定义一个准确率函数,这个可以在训练的时候输出分类的准确率
acc = fluid.layers.accuracy(input=model, label=label)接着是定义优化方法,这次我们使用的是Adam优化方法,同时指定学习率为0.001。
optimizer = fluid.optimizer.AdamOptimizer(learning_rate=0.001)#使用Adam算法进行优化
opts = optimizer.minimize(avg_cost)定义一个使用CPU的解析器
place = fluid.CPUPlace()
exe = fluid.Executor(place)参数初始化
exe.run(fluid.default_startup_program())定义输入数据维度
输入数据的维度是图像数据和图像对应的标签,每个类别的图像都要对应一个标签,这个标签是从0开始递增的整形值
feeder = fluid.DataFeeder(place=place, feed_list=[image, label])下面开始训练并测试
我们这次训练5个Pass,并且在每一轮Pass之后在进行一次测试,使用测试集进行测试,并求出当前的cost和准确率的average
for pass_id in range(5):
# 进行训练
for batch_id, data in enumerate(train_reader()): #遍历train_reader
train_cost, train_acc = exe.run(program=fluid.default_main_program(),#运行主程序
feed=feeder.feed(data), #给模型喂入数据
fetch_list=[avg_cost, acc])#fetch 误差、准确率
# 每100个batch打印一次信息 误差、准确率
if batch_id % 100 == 0:
print('Pass:%d, Batch:%d, Cost:%0.5f, Accuracy:%0.5f' %
(pass_id, batch_id, train_cost[0], train_acc[0]))
# 进行测试
test_accs = []
test_costs = []
#每训练一轮 进行一次测试
for batch_id, data in enumerate(test_reader()): #遍历test_reader
test_cost, test_acc = exe.run(program=fluid.default_main_program(), #执行训练程序
feed=feeder.feed(data), #喂入数据
fetch_list=[avg_cost, acc]) #fetch 误差、准确率
test_accs.append(test_acc[0]) #每个batch的准确率
test_costs.append(test_cost[0]) #每个batch的误差
# 求测试结果的平均值
test_cost = (sum(test_costs) / len(test_costs)) #每轮的平均误差
test_acc = (sum(test_accs) / len(test_accs)) #每轮的平均准确率
print('Test:%d, Cost:%0.5f, Accuracy:%0.5f' % (pass_id, test_cost, test_acc))
# 保存模型
model_save_dir = "./hand.inference.model"
# 如果保存路径不存在就创建
if not os.path.exists(model_save_dir):
os.makedirs(model_save_dir)
print('save models to %s' % (model_save_dir))
fluid.io.save_inference_model(model_save_dir, # 保存推理model的路径
['image'], # 推理(inference)需要 feed 的数据
[model], # 保存推理(inference)结果的 Variables
exe) # executor 保存 inference model先运行以下看下输出
Pass:0, Batch:0, Cost:2.50275, Accuracy:0.07812
Pass:0, Batch:100, Cost:0.32129, Accuracy:0.89062
Pass:0, Batch:200, Cost:0.28232, Accuracy:0.89062
Pass:0, Batch:300, Cost:0.30894, Accuracy:0.90625
Pass:0, Batch:400, Cost:0.23480, Accuracy:0.92188
Test:0, Cost:0.22551, Accuracy:0.93068
save models to ./hand.inference.model
Pass:1, Batch:0, Cost:0.21532, Accuracy:0.91406
Pass:1, Batch:100, Cost:0.25423, Accuracy:0.92188
Pass:1, Batch:200, Cost:0.16427, Accuracy:0.96094
Pass:1, Batch:300, Cost:0.12058, Accuracy:0.96875
Pass:1, Batch:400, Cost:0.13565, Accuracy:0.94531
Test:1, Cost:0.14589, Accuracy:0.95481
save models to ./hand.inference.model
Pass:2, Batch:0, Cost:0.14125, Accuracy:0.95312
Pass:2, Batch:100, Cost:0.14312, Accuracy:0.96094
Pass:2, Batch:200, Cost:0.07529, Accuracy:0.96875
Pass:2, Batch:300, Cost:0.10757, Accuracy:0.96094
Pass:2, Batch:400, Cost:0.19855, Accuracy:0.94531
Test:2, Cost:0.11291, Accuracy:0.96242
save models to ./hand.inference.model
Pass:3, Batch:0, Cost:0.10000, Accuracy:0.96875
Pass:3, Batch:100, Cost:0.12072, Accuracy:0.96094
Pass:3, Batch:200, Cost:0.05219, Accuracy:0.97656
Pass:3, Batch:300, Cost:0.09506, Accuracy:0.97656
Pass:3, Batch:400, Cost:0.13533, Accuracy:0.95312
Test:3, Cost:0.09648, Accuracy:0.96915
save models to ./hand.inference.model
Pass:4, Batch:0, Cost:0.18229, Accuracy:0.95312
Pass:4, Batch:100, Cost:0.12360, Accuracy:0.96875
Pass:4, Batch:200, Cost:0.10631, Accuracy:0.96875
Pass:4, Batch:300, Cost:0.10291, Accuracy:0.97656
Pass:4, Batch:400, Cost:0.06706, Accuracy:0.97656
Test:4, Cost:0.07825, Accuracy:0.97498
save models to ./hand.inference.model可以看到最终损失率在不断减小,准确率在不断接近1
4.模型预测
在预测之前,要对图像进行预处理,处理方式要跟训练时的一样
首先进行灰度化,然后压缩图像大小为28*28,接着将图像转换成一维向量,最后对一维向量进行归一化处理
def load_image(file):
#将RGB转化为灰度图像,L代表灰度图像,灰度图像的像素值在0~255之间
im = Image.open(file).convert('L')
im = im.resize((28,28), Image.ANTIALIAS) #resize image with high-quality 图像大小为28*28
#返回新形状的数组,把它变成一个 numpy 数组以匹配数据馈送格式。
im = np.array(im).reshape(1,1,28,28).astype(np.float32)
im = im / 255.0 * 2.0 -1.0 #归一化到【-1~1】之间
print(im)
return im
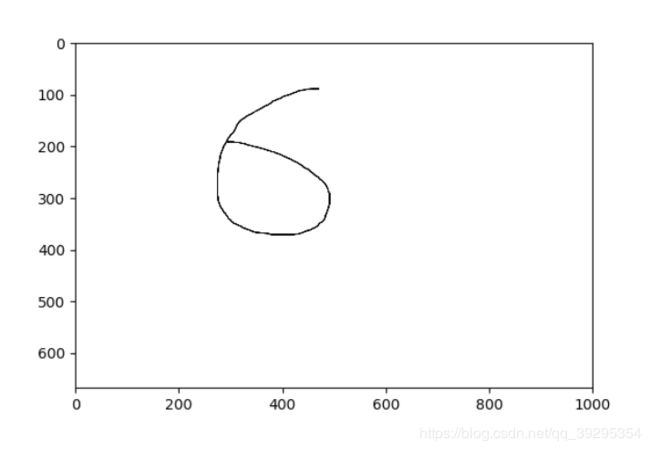
img = Image.open('./6.png')
plt.imshow(img) #根据数组绘制图像
plt.show() #显示图像运行一下看下结果:原图像随便用画图板画的
已经转换成功,将刚三行代码注释掉
重新定义一个CPU解析器并预测作用域
infer_exe = fluid.Executor(place)
inference_scope = fluid.core.Scope() #预测作用域加载数据并开始预测
with fluid.scope_guard(inference_scope):
#获取训练好的模型
#从指定目录中加载 推理model(inference model)
[inference_program,#推理Program
feed_target_names,#是一个str列表,它包含需要在推理 Program 中提供数据的变量的名称。
fetch_targets #fetch_targets:是一个 Variable 列表,从中我们可以得到推断结果。
] = fluid.io.load_inference_model(
model_save_dir,#model_save_dir:模型保存的路径
infer_exe)#infer_exe: 运行 inference model的 executor
img = load_image('./6.png')
results = exe.run(program=inference_program,#运行推测程序
feed={feed_target_names[0]:img}, #喂入要预测的img
fetch_list=fetch_targets) #得到推测结果获取概率最大的label
lab = np.argsort(results)#argsort函数返回的是result数组值从小到大的索引值
print("该图片的预测结果的label是:%d" % lab[0][0][-1]) #-1代表读取数组中倒数第一列开始运行:打印结果为
该图片的预测结果的label是:0又运行了几次,有1,有3,就是没有6......
换张图片试一下,这次用粗笔画的6,最后...