利用keras在时间步与维度上同时实现注意力机制的LSTM模型

注意力机制实现方法

现在已经有很多篇文章对注意力机制进行了介绍，简单来说，注意力机制可以通过下面操作实现：
引入一层激活函数为softmax的全连接层，输出一组权重来代表注意力，之后将原始输入与权重进行组合。很多博客在keras实现上借鉴了github的这个项目。
我在用keras搭建的LSTM网络训练一个物理模型时，输入数据是多个时间步的多个物理量，感觉可以用注意力机制对不同时间步和物理量提前分配权重，让结果更好反映出物理本质。但是目前看见的注意力模型都是只对时间步应用注意力机制，或者只对维度应用注意力机制，所以我稍微改进下常见的注意力层，对时间步和维度都应用了注意力机制。

测试数据

博文【深度学习】 基于Keras的Attention机制代码实现及剖析——LSTM+Attention中，作者对注意力机制进行了详细的实验。参考文中的方法，先写一个生成数据的函数。

def get_data_recurrent(n, time_steps, input_dim, attention_column=10,attention_index=4):
    x = np.random.standard_normal(size=(n, time_steps, input_dim))  # 标准正态分布随机特征值
    y = np.random.randint(low=0, high=2, size=(n, 1))  # 二分类，随机标签值
    # print(x[:,1,1].shape)
    # print(y[:].shape)
    x[:, attention_column, attention_index] = np.reshape(y[:],len(y))  
    return x, y

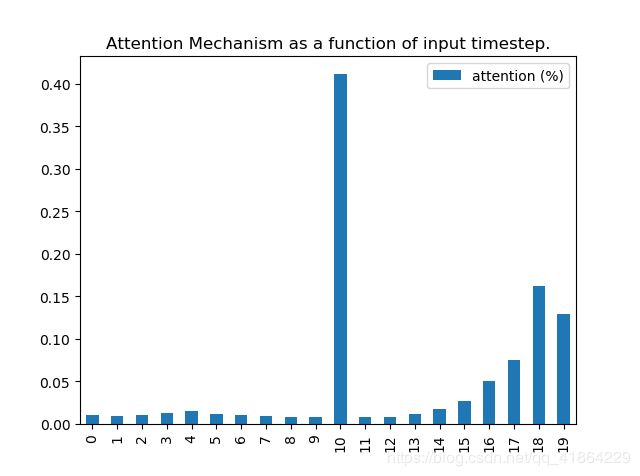
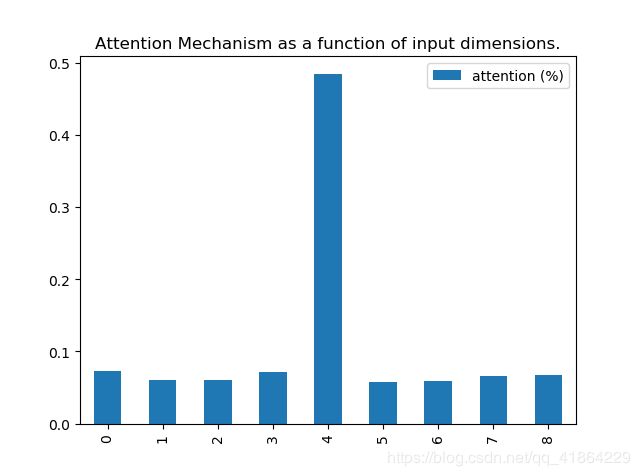
上述程序中n为生成的大小，input_dim为维度，timestep为时间步数，本次取输入为n= 30000, input_dim = 9 ,timesteps = 20。其中第timestep=11，input_dim=9时，x的值与y相同。

注意力层构造

博文【深度学习】 基于Keras的Attention机制代码实现及剖析——LSTM+Attention中只对时间步应用注意力机制的层如下

def attention_3d_block(inputs):
    # inputs.shape = (batch_size, time_steps, input_dim)
    input_dim = int(inputs.shape[2])
    a = Permute((2, 1))(inputs)
    a = Reshape((input_dim, TIME_STEPS))(a) # this line is not useful. It's just to know which dimension is what.
    a = Dense(TIME_STEPS, activation='softmax')(a)
    if SINGLE_ATTENTION_VECTOR:
        a = Lambda(lambda x: K.mean(x, axis=1), name='dim_reduction')(a)
        a = RepeatVector(input_dim)(a)
    a_probs = Permute((2, 1), name='attention_vec')(a)
    output_attention_mul = Multiply()([inputs, a_probs])
    return output_attention_mul

若要在维度和时间步同时分配注意力，本次选择采用以下步骤：

1、先对原始输入，通过两个全连接层，分别计算对时间步和维度的注意力分配矩阵A、B，对本次的原始输入，注意力分配矩阵为：

$$A={\begin{array}{c}\left[\begin{array}{cccc}{a}_1& a_1& ...& a_1\\ a_2& a_2& ...& a_2\\ .& & & .\\ .& & & .\\ .& & & .\\ a_{20}& a_{20}& ...& a_{20}\end{array}\right]\end{array}}_{20\times 9},\sum _{n=1}^{20}{a}_n=1$$

$$B={\begin{array}{c}\left[\begin{array}{cccc}{b}_1& b_2& ...& b_9\\ b_1& b_2& ...& b_9\\ .& & & \\ .& & & \\ b_1& b_2& ...& b_9\end{array}\right]\end{array}}_{20\times 9},\sum _{n=1}^9{b}_n=1,$$

最后的注意力权重为A、B的逐元素积
$${\begin{array}{c}\left[\begin{array}{cccc}{a}_1\times b_1& a1\times b_2& ...& a_1\times b_9\\ a_2\times b_1& a_2\times b_2& ...& a_2\times b_9\\ .& & & \\ .& & & \\ a_{20}\times b_1& a_{20}\times b_2& ...& a_{20}\times b_9\end{array}\right]\end{array}}_{20\times 9}$$
上述矩阵与原始输入逐元素积得到注意力层的输出。
注意力层的子程序为：

def attention_3d_block_method2(inputs):
    # inputs.shape = (batch_size, time_steps, input_dim)
    input_dim = int(inputs.shape[2])
    a1 = Permute((2, 1))(inputs)
    # a1 = Reshape((input_dim, TIME_STEPS))(a1)  # this line is not useful. It's just to know which dimension is what.
    a1 = Dense(TIME_STEPS, activation='softmax')(a1)
    a1 = Lambda(lambda x: K.mean(x, axis=1))(a1)
    a1 = RepeatVector(input_dim)(a1)
    a1 = Permute((2,1),name='attention_vec1')(a1)
    a2 = Dense(input_dim, activation='softmax',name='attention_vec2')(inputs)
    a2 = Lambda(lambda x: K.mean(x, axis=1))(a2)
    a2 = RepeatVector(TIME_STEPS)(a2)
    a_probs = Multiply()([a1,a2])
    output_attention_mul = Multiply()([inputs, a_probs])
    return output_attention_mul

完整的模型程序为：

def model_attention_applied_before_lstm():
    K.clear_session()  # 清除之前的模型，省得压满内存
    inputs = Input(shape=(TIME_STEPS, INPUT_DIM,))
    attention_mul = attention_3d_block_method2(inputs)
    # attention_mul = attention_3d_block(inputs)
    lstm_units = 32
    attention_mul = LSTM(lstm_units, return_sequences=False)(attention_mul)
    output = Dense(1, activation='sigmoid')(attention_mul)
    model = Model(input=[inputs], output=output)
    return model

结果

结果表明这种注意力层可以对维度和时间步分别分配注意力权重。