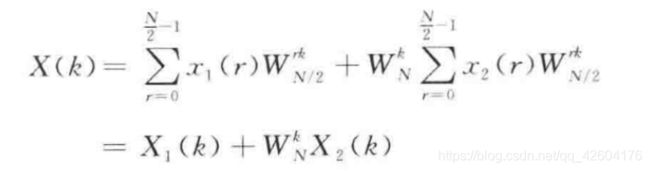- 迷你世界脚本出生点接口:Spawnport
星空露珠
笔记lua游戏数据结构
出生点接口:Spawnport彼得兔更新时间:2023-04-2610:19:56具体函数名及描述如下:序号函数名函数描述1getSpawnPoint(...)获取默认出生点2setSpawnPoint(...)设置出生点位置3getChunkValidSpawnPos(...)获取区块有效刷新点,可作为出生点getSpawnPoint参数及类型:nil返回值及类型:ErrorCode.OKx:n
- CocoaPods错误:CDN: trunk URL couldn't be downloaded:......(Connection refused
auspark
cocoapod
执行podsearch时候出错:$podsearchYYWebImage报错信息:CDN:trunkURLcouldn'tbedownloaded:https://raw.githubusercontent.com/CocoaPods/Specs/master/Specs/4/c/8/YYWebImage/1.0.3/YYWebImage.podspec.json,error:Failedtoop
- 嵌入式开发:傅里叶变换(4):在 STM32上面实现FFT(基于STM32L071KZT6 HAL库+DSP库)
魂兮-龙游
嵌入式开发stm32嵌入式硬件单片机DSP库数字信号处理
目录步骤1:准备工作步骤2:创建Keil项目,并配置工程步骤3:在MDK工程上添加CMSIS-DSP库步骤5:编写代码步骤6:配置时钟和优化步骤7:调试与验证步骤8:优化和调整注意事项:在STM32L071KZT6上使用MDK(KeiluVision)移植DSP库源码,并且基于HAL库进行开发,可以按照以下步骤进行操作:步骤1:准备工作安装KeilMDK:。安装STM32CubeMX:参考博客:S
- 【AHK】资源管理器自动化办公实例/自动连点设置
LAM LAB
AHK自动化运维
此处为一个自动连续点击打开检查的自动化操作案例,没有quicker的鼠键录制,不常用了,做个备份#MaxThreadsPerHotkey2;这个是核心!!!!确保可以同时运行多个热键或标签globalisRunning:=truef4::;假设我们使用Ctrl+J作为热键来切换循环的状态if(isRunning){isRunning:=falseMsgBox,循环已停止}else{isRunnin
- 【微服务-SpringCloud】详细介绍,搭建一套微服务项目
Tank_Chen
Springjavaspringbootspringcloud
目录微服务介绍微服务的特点微服务的优势微服务的挑战SpringCloud介绍SpringCloud核心概念为什么使用SpringCloudSpringCloud使用项目案例技术栈环境准备创建项目用户服务(UserService)pom.xmlapplication.ymlUserController.javaUserService启动类订单服务(OrderService)pom.xmlapplic
- 微服务实战:Spring Boot与Spring Cloud指南
萧书泓
微服务实战:SpringBoot与SpringCloud指南Microservices-with-Spring-Boot-and-Spring-Cloud-Third-EditionMicroserviceswithSpringBootandSpringCloud,ThirdEdition项目地址:https://gitcode.com/gh_mirrors/mi/Microservices-wi
- WPF7-布局元素
Zy100Papa
wpf.netxamlc#
目录1.WPF布局原则--不应设置具体大小2.WPF中布局容器2.1.Grid控件(网格布局)2.2.StackPanel控件(栈式布局)2.3.WrapPanel控件(环绕布局)2.4.DockPanel控件(停靠布局)2.5.Canvas面板控件(绝对定位布局)2.6.UniformGrid控件2.7.GridSplitter网格分割器2.8.TabPanel:选项卡面板1.WPF布局原则–不
- 利用DSPy优化LangChain RAG系统的实战指南
scaFHIO
langchainpython
利用DSPy优化LangChainRAG系统的实战指南技术背景介绍DSPy是一个用于大语言模型(LLMs)的出色框架,它引入了一个自动编译器,能够教会模型如何执行你程序中的声明性步骤。具体来说,DSPy编译器会在内部追踪你的程序,然后为大型语言模型(LLMs)创建高质量的提示(或为小型LLMs训练自动微调),以教会它们任务的步骤。感谢OmarKhattab的努力,现在DSPy可以与LangChai
- sentinel 使用说明
o_瓜田李下_o
springcloudalibabasentinelsentinel
sentinel使用说明相关依赖com.alibaba.cloudspring-cloud-starter-alibaba-sentinelcom.alibaba.cspsentinel-apache-dubbo-adaptercom.alibaba.cloudspring-cloud-alibaba-sentinel-datasourcecom.alibaba.cloudspring-cloud
- 芯片中常见的缩写
yyc_audio
其他嵌入式硬件
IC(integratedcircuit):集成电路ASP(applicationspecificprocessor):在特定应用领域使用的DSPSDRAM(SynchronousDynamicRandomAccessMemory):同步动态随机存取存储器DDR(DoubleDataRateSDRAM):双倍速率同步动态随机存储器(内存的一种)DMA(DirectMemoryAccess):直接存
- STM32F407开发板模块端口介绍
黄卷青灯77
stm32嵌入式硬件单片机
普中STM32F407开发板,不带LCD的开发板如图2-8所示。开发板上有两个MCU,一个是STM32F407ZGT6芯片(FPU+DSP,LQFP144封装,1024KBFlash,196KBSRAM),另一个是STM32F103C8T6芯片(LQFP48封装,64KBFlash,20KBSRAM)。开发板上有两个MCU,适合于做一些双机主从通信的开发实验,如USART通信、SPI主从通信。在图
- 嵌入式开发:傅里叶变换(5):基于STM32-DSP库实现
魂兮-龙游
嵌入式开发FFT快速傅里叶变换滤波数字信号处理嵌入式开发物联网
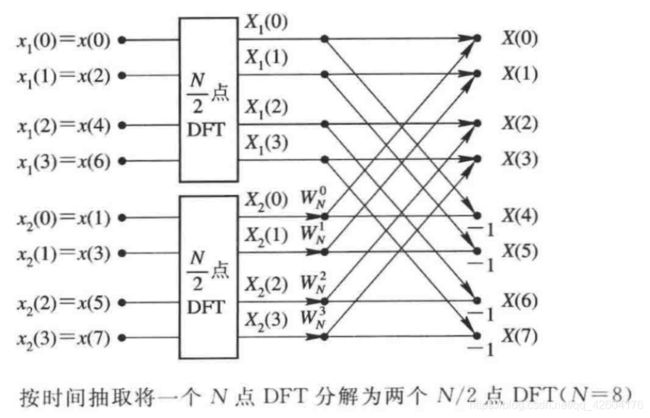
目录1.准备工作2.函数介绍1.arm_rfft_instance_f32结构体2.arm_rfft_fast_init_f32函数3.arm_rfft_fast_f32函数4.FFT的执行过程4.编写FFT实现代码4.1初始化FFT实例4.2配置FFT长度和初始化实例4.3填充输入数据4.4执行FFT4.5处理结果5.主函数6.编译和调试7.总结在STM32上使用CMSIS-DSP库实现快速傅里
- 部署 Llama 3.1 405B:分步指南,深入研究 Llama 最新模型 Llama 3.1 4050 亿参数模型的部署。这个强大的模型需要大量的 VRAM,特别是 4 位量化版本需要 231 G
知识大胖
NVIDIAGPU和大语言模型开发教程llamaai
简介今天,我们将深入研究Llama最新模型Llama3.14050亿参数模型的部署。这个强大的模型需要大量的VRAM,特别是4位量化版本需要231GB。但是,经过一些优化,我们可以使用8x4090GPU在192GB上运行它。最好的部分?我们只需要运行三个终端命令即可完成所有设置。推荐文章《使用DSPy、Qdrant和Llama3对复杂问题进行多跳检索和推理,利用DSPy的无提示框架进行复杂的LLM
- Destroy Component只能销毁自己所在actor
mmmmmdywe
#生命周期c++ue5
DestroyComponent只能销毁自己所在actor1我在使用Spline制作抛物线时,发现当我要销毁spline上的SplineMeshComponent时,销毁不了。后修改AddSplinemeshComponent的Target为Self时,就可以销毁了。我就奇怪,去看看这个节点的注释:不能销毁被一个Actor拥有的Component,除非这个Actor正在调用这个节点。这下明白了,这
- 前端安装依赖报错【certificate has expired】解决办法
ZuuuuYao
开发工具前端前端
报错信息:yarninstallv1.22.22warningpackage.json:LicenseshouldbeavalidSPDXlicenseexpressioninfoNolockfilefound.warningdatareport.front@3.7.0:LicenseshouldbeavalidSPDXlicenseexpression[1/4]Resolvingpackages
- SpringBoot 整合 Avro 与 Kafka
m0_74823595
面试学习路线阿里巴巴springbootkafkalinq
优质博文:IT-BLOG-CN【需求】:生产者发送数据至kafka序列化使用Avro,消费者通过Avro进行反序列化,并将数据通过MyBatisPlus存入数据库。一、环境介绍【1】ApacheAvro1.8;【2】SpringKafka1.2;【3】SpringBoot1.5;【4】Maven3.5;4.0.0com.codenotfoundspring-kafka-avro0.0.1-SNAP
- 对应chd5.14的spark_carbonData使用文档(基于CDH 的spark-yarn模式)
颜语一声
对应chd5.14的spark
一、部署(基于CDH的spark-yarn模式)下载源码编译(目前官网已经提供编译好的jar包了)【https://dist.apache.org/repos/dist/release/carbondata/】mvn-DskipTests-Pspark-2.1-Dspark.version=2.1.0cleanpackagemvn-DskipTests-Pspark-2.2-Dspark.vers
- SpringCloud03—服务治理:SpringCloud Eureka
m0_75011249
程序员springcloudeurekajava
《一线大厂Java面试题解析+核心总结学习笔记+最新讲解视频+实战项目源码》,点击传送门,即可获取!spring-boot-starter-parent2.5.1org.springframework.cloudspring-cloud-starter-eureka1.4.7.RELEASEorg.springframework.cloudspring-cloud-dependencies2020
- Spark源码分析
陈同学�
sparkbigdatascala
Spark源码分析SparkonYarnclientCluster本质区别,driver位置不同1)有哪些不同得进程?2)分别有什么作用?3)Spark作业执行流程是什么样的跑yarn有--masteryarnCoarseGrainedExecutorBackend默认executor有两个CoarseGrainedExecutorBackendSparkSubmitApplicationMast
- 嵌入式MCU平台汇总
TENET-
嵌入式单片机嵌入式硬件mcu
文章目录1.单片机(MCU)2.数字信号处理器(DSP)3.ARMCortex系列4.超低功耗MCU5.物联网MCU(IoTMCU)6.开源架构MCU(RISC-V)7.可编程逻辑器件(FPGA)1.单片机(MCU)概念:单片机(MicrocontrollerUnit,MCU)是集成了中央处理器(CPU)、存储器(RAM、ROM或Flash)、输入输出端口(I/O)以及各种外设(如定时器、串行通信
- 青稞RISC-V通用系列
ws137517175
risc-v
青稞RISC-V通用系列的特点:高性能与低功耗:青稞系列处理器针对不同应用场景进行了优化,能够在提供高性能的同时保持低功耗,适合电池供电的设备和物联网终端。模块化设计:青稞系列采用模块化设计,用户可以根据需求选择不同的功能模块,如浮点运算单元(FPU)、数字信号处理(DSP)扩展、向量处理单元等。可扩展性:基于RISC-V的开放架构,青稞系列处理器支持用户自定义指令集扩展,能够满足特定应用场景的需
- 微服务网关springcloud gateway整合nacos实现服务名负载均衡
程序猿20
开发框架微服务gateway负载均衡nacos
1.添加依赖com.alibaba.cloudspring-cloud-starter-alibaba-nacos-discovery2.2.5.RELEASE2.添加配置spring:cloud:nacos:discovery:#服务注册地址server-addr:192.168.17.94:88483.将路由配置中的uri采用lb://服务名的形式进行配置spring:cloud:gatewa
- 【异常】SpringAI提示 Failed to download spring-ai-core 无法解析 org.springframework.ai:spring-ai-core:1.0.0-M3
本本本添哥
002-进阶开发能力013-AIGC人工智能大模型spring人工智能java
一、报错内容[WARNING]Failedtodownloadspring-ai-core-1.0.0-M3.jar[https://repo.spring.io/milestone/][WARNING]Failedtodownloadspring-ai-core-1.0.0-M3.jar[https://repo.maven.apache.org/maven2/]无法解析org.springfr
- Spring Boot 整合 Kafka 详解
码农爱java
KafkaKafkaMQSpringBoot微服务中间件1024程序员节
前言:上一篇分享了Kafka的一些基本概念及应用场景,本篇我们来分享一下在SpringBoot项目中如何使用Kafka。Kafka系列文章传送门Kafka简介及核心概念讲解SpringBoot集成Kafka引入Kafka依赖在项目的pom.xml文件中引入Kafka依赖,如下:org.springframework.cloudspring-cloud-starter-stream-kafka3.1
- 【数值模型后处理系列】通风系数计算及垂直层插值
北潇
数值模型Python实用基础技能pythonWRF
一、通风系数1.1通风系数简介通风系数(VentilationCoefficient,VC)可以用来表征扩散条件,其计算公式如下(参考USIyerandPErnestRaj的文章):其中mixingdepth选用WRF输出的边界层高度(PBLH),meanwindspeed近似用边界层顶的风速与地面风速做平均(当然也可多选几层)。1.2Python代码实现VC的计算计算VC的示例代码:fromne
- 深入解析Spring Cloud:微服务架构的利器(上)
Wells974
爪哇架构springcloud微服务
随着互联网应用的不断发展,单体应用架构逐渐难以满足业务快速迭代和扩展的需求。微服务架构因其良好的可扩展性和灵活性,逐渐成为现代应用的主流架构。而SpringCloud作为一套微服务开发的全家桶,提供了完整的微服务解决方案。本文将详细介绍SpringCloud的基本概念、核心组件及其在微服务架构中的应用。1.SpringCloud的基本概念1.1什么是SpringCloudSpringCloud是基
- Xilinx FPGA开发指南-7系列FPGA配置引脚定义(草稿)
RunningCamel
fpga开发
目录配置引脚定义表配置引脚定义表配置引脚定义表引脚名称BANK类型方向描述CFGBVS0专用引脚Input配置组电压选择CFGBVS确定专用配置组0的I/O电压工作范围和电压容限,以及AMDSpartan™-7,AMDArtix™-7和AMDKintex™-7系列中银行14和15的多功能配置引脚。CFGBVS在所有7系列器件中始终为专用组0选择工作电压。CFGBVS只在配置时选择多功能配置组14和
- DSP和ARM的优劣比较(也有FPGA)
bingfeng_adonis
工作
概念1.FPGA:是可编程逻辑阵列,常用于处理高速数字信号,不过随着科技的发展,现在很多FPGACPLD可以集成mcu内核,甚至具备了ARMDSP的功能2.ARM,是一类内核的称谓,就像51一样,具体到芯片的话,会有很多不同的厂家不同等级,诸如三星、易法、飞利浦、摩托罗拉等等,其中STM32是易法半导体的一款面向工控低功耗内核为CortexM3内核的ARM芯片3.DSP顾名思义就是数字信号处理,厂
- Spring Cloud Stream与RabbitMQ 死信队列
y_bccl27
RabbitMQ
RabbitMQ的TTL全称为Time-To-Live,表示的是消息的有效期。消息如果在队列中一直没有被消费并且存在时间超过了TTL,消息就会变成"死信"(DeadMessage),后续无法再被消费。引入SpringCloudStream与RabbitMQ整合的pom依赖,其版本为3.0.7.RELEASEorg.springframework.cloudspring-cloud-starter-
- Python爬虫+数据分析:采集二手房源数据并做可视化
嘘!摸鱼中~
爬虫小案例数据分析小案例python数据分析开发语言学习
目录软件使用:模块使用:代码展示尾语今天我们来分享一个用Python采集二手房源数据信息并做可视化得源码软件使用:python3.8开源免费的(统一3.8)jupyter-->pipinstalljupyternotebookPycharmYYDSpython最好用的编辑器不接受反驳…(也可以使用)模块使用:第三方:requests>>>数据请求模块parsel>>>数据解析模块内置:csv内置模
- java线程Thread和Runnable区别和联系
zx_code
javajvmthread多线程Runnable
我们都晓得java实现线程2种方式,一个是继承Thread,另一个是实现Runnable。
模拟窗口买票,第一例子继承thread,代码如下
package thread;
public class ThreadTest {
public static void main(String[] args) {
Thread1 t1 = new Thread1(
- 【转】JSON与XML的区别比较
丁_新
jsonxml
1.定义介绍
(1).XML定义
扩展标记语言 (Extensible Markup Language, XML) ,用于标记电子文件使其具有结构性的标记语言,可以用来标记数据、定义数据类型,是一种允许用户对自己的标记语言进行定义的源语言。 XML使用DTD(document type definition)文档类型定义来组织数据;格式统一,跨平台和语言,早已成为业界公认的标准。
XML是标
- c++ 实现五种基础的排序算法
CrazyMizzz
C++c算法
#include<iostream>
using namespace std;
//辅助函数,交换两数之值
template<class T>
void mySwap(T &x, T &y){
T temp = x;
x = y;
y = temp;
}
const int size = 10;
//一、用直接插入排
- 我的软件
麦田的设计者
我的软件音乐类娱乐放松
这是我写的一款app软件,耗时三个月,是一个根据央视节目开门大吉改变的,提供音调,猜歌曲名。1、手机拥有者在android手机市场下载本APP,同意权限,安装到手机上。2、游客初次进入时会有引导页面提醒用户注册。(同时软件自动播放背景音乐)。3、用户登录到主页后,会有五个模块。a、点击不胫而走,用户得到开门大吉首页部分新闻,点击进入有新闻详情。b、
- linux awk命令详解
被触发
linux awk
awk是行处理器: 相比较屏幕处理的优点,在处理庞大文件时不会出现内存溢出或是处理缓慢的问题,通常用来格式化文本信息
awk处理过程: 依次对每一行进行处理,然后输出
awk命令形式:
awk [-F|-f|-v] ‘BEGIN{} //{command1; command2} END{}’ file
[-F|-f|-v]大参数,-F指定分隔符,-f调用脚本,-v定义变量 var=val
- 各种语言比较
_wy_
编程语言
Java Ruby PHP 擅长领域
- oracle 中数据类型为clob的编辑
知了ing
oracle clob
public void updateKpiStatus(String kpiStatus,String taskId){
Connection dbc=null;
Statement stmt=null;
PreparedStatement ps=null;
try {
dbc = new DBConn().getNewConnection();
//stmt = db
- 分布式服务框架 Zookeeper -- 管理分布式环境中的数据
矮蛋蛋
zookeeper
原文地址:
http://www.ibm.com/developerworks/cn/opensource/os-cn-zookeeper/
安装和配置详解
本文介绍的 Zookeeper 是以 3.2.2 这个稳定版本为基础,最新的版本可以通过官网 http://hadoop.apache.org/zookeeper/来获取,Zookeeper 的安装非常简单,下面将从单机模式和集群模式两
- tomcat数据源
alafqq
tomcat
数据库
JNDI(Java Naming and Directory Interface,Java命名和目录接口)是一组在Java应用中访问命名和目录服务的API。
没有使用JNDI时我用要这样连接数据库:
03. Class.forName("com.mysql.jdbc.Driver");
04. conn
- 遍历的方法
百合不是茶
遍历
遍历
在java的泛
- linux查看硬件信息的命令
bijian1013
linux
linux查看硬件信息的命令
一.查看CPU:
cat /proc/cpuinfo
二.查看内存:
free
三.查看硬盘:
df
linux下查看硬件信息
1、lspci 列出所有PCI 设备;
lspci - list all PCI devices:列出机器中的PCI设备(声卡、显卡、Modem、网卡、USB、主板集成设备也能
- java常见的ClassNotFoundException
bijian1013
java
1.java.lang.ClassNotFoundException: org.apache.commons.logging.LogFactory 添加包common-logging.jar2.java.lang.ClassNotFoundException: javax.transaction.Synchronization
- 【Gson五】日期对象的序列化和反序列化
bit1129
反序列化
对日期类型的数据进行序列化和反序列化时,需要考虑如下问题:
1. 序列化时,Date对象序列化的字符串日期格式如何
2. 反序列化时,把日期字符串序列化为Date对象,也需要考虑日期格式问题
3. Date A -> str -> Date B,A和B对象是否equals
默认序列化和反序列化
import com
- 【Spark八十六】Spark Streaming之DStream vs. InputDStream
bit1129
Stream
1. DStream的类说明文档:
/**
* A Discretized Stream (DStream), the basic abstraction in Spark Streaming, is a continuous
* sequence of RDDs (of the same type) representing a continuous st
- 通过nginx获取header信息
ronin47
nginx header
1. 提取整个的Cookies内容到一个变量,然后可以在需要时引用,比如记录到日志里面,
if ( $http_cookie ~* "(.*)$") {
set $all_cookie $1;
}
变量$all_cookie就获得了cookie的值,可以用于运算了
- java-65.输入数字n,按顺序输出从1最大的n位10进制数。比如输入3,则输出1、2、3一直到最大的3位数即999
bylijinnan
java
参考了网上的http://blog.csdn.net/peasking_dd/article/details/6342984
写了个java版的:
public class Print_1_To_NDigit {
/**
* Q65.输入数字n,按顺序输出从1最大的n位10进制数。比如输入3,则输出1、2、3一直到最大的3位数即999
* 1.使用字符串
- Netty源码学习-ReplayingDecoder
bylijinnan
javanetty
ReplayingDecoder是FrameDecoder的子类,不熟悉FrameDecoder的,可以先看看
http://bylijinnan.iteye.com/blog/1982618
API说,ReplayingDecoder简化了操作,比如:
FrameDecoder在decode时,需要判断数据是否接收完全:
public class IntegerH
- js特殊字符过滤
cngolon
js特殊字符js特殊字符过滤
1.js中用正则表达式 过滤特殊字符, 校验所有输入域是否含有特殊符号function stripscript(s) { var pattern = new RegExp("[`~!@#$^&*()=|{}':;',\\[\\].<>/?~!@#¥……&*()——|{}【】‘;:”“'。,、?]"
- hibernate使用sql查询
ctrain
Hibernate
import java.util.Iterator;
import java.util.List;
import java.util.Map;
import org.hibernate.Hibernate;
import org.hibernate.SQLQuery;
import org.hibernate.Session;
import org.hibernate.Transa
- linux shell脚本中切换用户执行命令方法
daizj
linuxshell命令切换用户
经常在写shell脚本时,会碰到要以另外一个用户来执行相关命令,其方法简单记下:
1、执行单个命令:su - user -c "command"
如:下面命令是以test用户在/data目录下创建test123目录
[root@slave19 /data]# su - test -c "mkdir /data/test123"
- 好的代码里只要一个 return 语句
dcj3sjt126com
return
别再这样写了:public boolean foo() { if (true) { return true; } else { return false;
- Android动画效果学习
dcj3sjt126com
android
1、透明动画效果
方法一:代码实现
public View onCreateView(LayoutInflater inflater, ViewGroup container, Bundle savedInstanceState)
{
View rootView = inflater.inflate(R.layout.fragment_main, container, fals
- linux复习笔记之bash shell (4)管道命令
eksliang
linux管道命令汇总linux管道命令linux常用管道命令
转载请出自出处:
http://eksliang.iteye.com/blog/2105461
bash命令执行的完毕以后,通常这个命令都会有返回结果,怎么对这个返回的结果做一些操作呢?那就得用管道命令‘|’。
上面那段话,简单说了下管道命令的作用,那什么事管道命令呢?
答:非常的经典的一句话,记住了,何为管
- Android系统中自定义按键的短按、双击、长按事件
gqdy365
android
在项目中碰到这样的问题:
由于系统中的按键在底层做了重新定义或者新增了按键,此时需要在APP层对按键事件(keyevent)做分解处理,模拟Android系统做法,把keyevent分解成:
1、单击事件:就是普通key的单击;
2、双击事件:500ms内同一按键单击两次;
3、长按事件:同一按键长按超过1000ms(系统中长按事件为500ms);
4、组合按键:两个以上按键同时按住;
- asp.net获取站点根目录下子目录的名称
hvt
.netC#asp.nethovertreeWeb Forms
使用Visual Studio建立一个.aspx文件(Web Forms),例如hovertree.aspx,在页面上加入一个ListBox代码如下:
<asp:ListBox runat="server" ID="lbKeleyiFolder" />
那么在页面上显示根目录子文件夹的代码如下:
string[] m_sub
- Eclipse程序员要掌握的常用快捷键
justjavac
javaeclipse快捷键ide
判断一个人的编程水平,就看他用键盘多,还是鼠标多。用键盘一是为了输入代码(当然了,也包括注释),再有就是熟练使用快捷键。 曾有人在豆瓣评
《卓有成效的程序员》:“人有多大懒,才有多大闲”。之前我整理了一个
程序员图书列表,目的也就是通过读书,让程序员变懒。 写道 程序员作为特殊的群体,有的人可以这么懒,懒到事情都交给机器去做,而有的人又可
- c++编程随记
lx.asymmetric
C++笔记
为了字体更好看,改变了格式……
&&运算符:
#include<iostream>
using namespace std;
int main(){
int a=-1,b=4,k;
k=(++a<0)&&!(b--
- linux标准IO缓冲机制研究
音频数据
linux
一、什么是缓存I/O(Buffered I/O)缓存I/O又被称作标准I/O,大多数文件系统默认I/O操作都是缓存I/O。在Linux的缓存I/O机制中,操作系统会将I/O的数据缓存在文件系统的页缓存(page cache)中,也就是说,数据会先被拷贝到操作系统内核的缓冲区中,然后才会从操作系统内核的缓冲区拷贝到应用程序的地址空间。1.缓存I/O有以下优点:A.缓存I/O使用了操作系统内核缓冲区,
- 随想 生活
暗黑小菠萝
生活
其实账户之前就申请了,但是决定要自己更新一些东西看也是最近。从毕业到现在已经一年了。没有进步是假的,但是有多大的进步可能只有我自己知道。
毕业的时候班里12个女生,真正最后做到软件开发的只要两个包括我,PS:我不是说测试不好。当时因为考研完全放弃找工作,考研失败,我想这只是我的借口。那个时候才想到为什么大学的时候不能好好的学习技术,增强自己的实战能力,以至于后来找工作比较费劲。我
- 我认为POJO是一个错误的概念
windshome
javaPOJO编程J2EE设计
这篇内容其实没有经过太多的深思熟虑,只是个人一时的感觉。从个人风格上来讲,我倾向简单质朴的设计开发理念;从方法论上,我更加倾向自顶向下的设计;从做事情的目标上来看,我追求质量优先,更愿意使用较为保守和稳妥的理念和方法。
&