基于二维矩阵的FFT计算原理
FFT算法是信号处理领域最基本、最经典的算法,在工程实践中用处十分广泛,但是在一些对FFT点数要求较大或者计算FFT实时性要求较高的场合,按常规方式直接计算FFT难以满足工程实际的要求。本文针对长点数FFT计算开发了一种基于二维矩阵的FFT算法,此算法将需要计算的复数点序列抽象为一个二维矩阵进行处理,将大点数计算分割为多次小点数FFT计算,并且小点数之间的处理互不影响,进而可在多核处理器(如多核DSP)或FPGA上并行执行,实时性将得到提高。
1.1理论推导
1.2算法步骤
通过1.1小节的推导我们可以总结出二维矩阵FFT算法的步骤:
1.将待计算序列划分为N1xN2二维矩阵;
2.进行N2次N1点的FFT;
3.将N2次N1点FFT结果乘铰链因子;
4.进行N1次N2点FFT;
5.译序。
1.3Matlab仿真实现
(1)将算法封装成一个函数,方便在其他程序中直接调用,编写程序时按照1.2中说明的步骤来进行,具体代码如下:
function X=FFT_2DMatrix(x,N,L,M)
%Function descirption:N points FFT based on two-dimention matrix(N=M*L)
%Input parameter: x,input time domain data
% N,points
% L,row of 2D matrix
% M,collum of 2D matrix
%Output parameter:X,output frequency domain data
%Created by Baokuo Liu,2020-4-3.All rights reserved.
x2=zeros(M,L);
for n1=1:L
for n0=1:M
x2(n1,n0)=x(1,(n1-1)*M+n0); %划分为L*M二维矩阵
end
end
X1=zeros(M,L);
X2=zeros(M,L);
rot_factor=zeros(M,L);
for i=1:M
X1(:,i)=fft(x2(:,i),L); %M列L点FFT
rot_factor(:,i)=exp(1j*2*pi*(i-1).*(0:L-1)/N)'; %旋转(铰链)因子
X2(:,i)=X1(:,i).*rot_factor(:,i); %FFT结果乘以旋转(铰链)因子
end
X3=zeros(M,L);
for i=1:L
X3(i,:)=fft(X2(i,:),M); %L列M点FFT
end
X=zeros(1,N);
for k0=1:L
for k1=1:M
X(1,(k1-1)*L+k0)=X3(k0,k1); %译序
end
end
(2)为了验证算法函数编写的正确性,仿真采样率为1.6kHz条件下,对频率100Hz的单频信号做256点FFT,调用上面的算法函数来完成FFT的计算,程序代码如下:
%parameter
N=256; %points
M=16; %collum of 2DMatrix
L=16; %row of 2DMatrix
fs=1600; %sample frequency
f0=100; %signal frequency
Vmax=1.8; %Max input voltage
Vamp=1; %amplitude
AD_bit=14; %AD bits
%generate single sine wave
t=0:1/fs:(N-1)/fs;
x=Vamp*sin(2*pi*f0.*t);
%quantify
x=round((2^(AD_bit)-1).*x/Vmax);
% output as a txt file(hex)
% x1=x';
% q=quantizer([AD_bit+1 0]);
% x2=num2bin(q,x1);
% fid1=fopen('C:\Users\radar\Desktop\Science\DSP\FFT_2DMatrix.txt','wt');
% for i=1:length(x)
% fwrite(fid1,x2(i,:));
% fprintf(fid1,'\n');
% end
% fclose(fid1);
%FFT based on two dimention matrix
f=(-N/2:1:N/2-1)*fs/N;
X=FFT_2DMatrix(x,N,L,M);
figure;
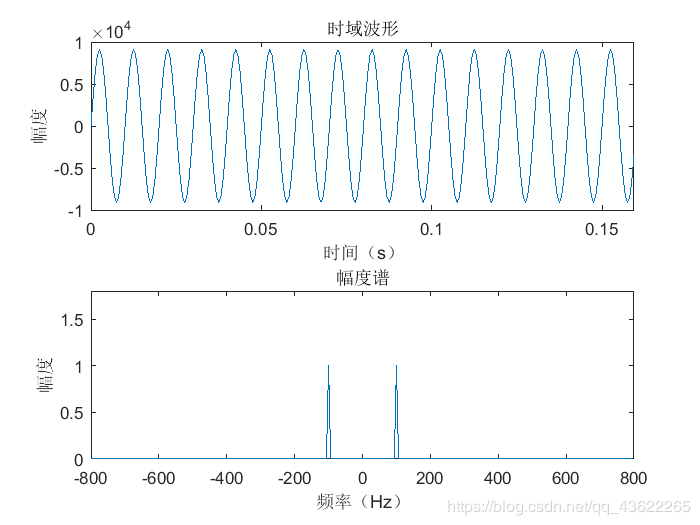
subplot(2,1,1);plot(t,x);xlabel('时间(s)');xlim([0 inf]);
ylabel('幅度');title('时域波形');
subplot(2,1,2);plot(f,abs(fftshift(X))*2/N*Vmax/(2^(AD_bit)-1));xlabel('频率(Hz)');
ylabel('幅度');ylim([0 1.8]);title('幅度谱');
1.4结果分析
仿真结果如上图所示,可见二维矩阵方法所得的FFT结果和常规一维点列FFT的结果完全一致,由此验证了算法程序编写的正确性。
1.5硬件实现
由于此2D-FFT算法在硬件实现上较复杂,不同处理器实现方法也不相同,这是暂时不做详细介绍,总的来说还是基于常规的一维FFT,读者可根据算法步骤自己尝试实现。对于在FPGA中的实现,可以参考我的另一篇博客:https://blog.csdn.net/qq_43622265/article/details/105905927,这篇博客是关于FFT IP核的使用方法,大家可以以此为基础来自行实现2D-FFT。
说明:理论推导部分参考了文献《基于TMS320C6678的多核DSP并行处理应用技术研究》,感兴趣的同学可到知网自行下载阅读。