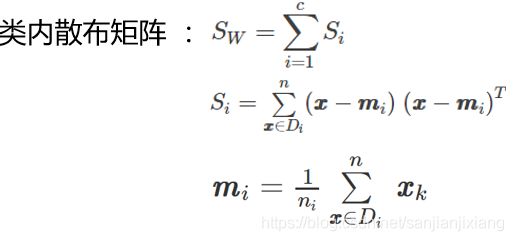sklearn降维1: 线性判别分析LDA原理python过程

import pandas as pd

#df = pd.read_csv('iris.data', header=None, sep=',')
df = pd.io.parsers.read_csv(filepath_or_buffer='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',header=None,sep=',')

feature_dict = {i:label for i,label in zip(range(4), ('sepal length', 'sepal width','petal lenth', 'petal width'))}
df.columns = [l for i,l in sorted(feature_dict.items())] + ['class label']
df.dropna(how = 'all', inplace = True)
df.head()

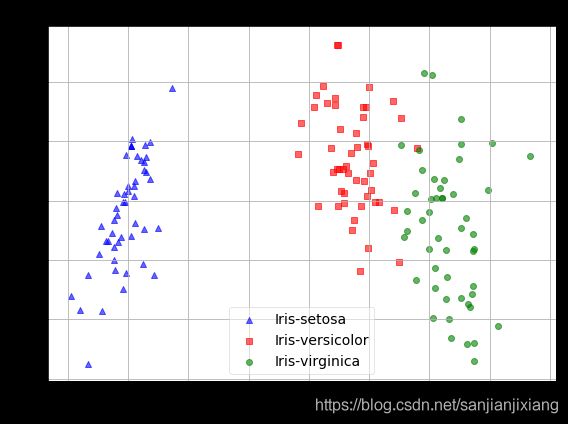
一. 求三种鸢尾花数据在不同特征维度上的均值向量

X = df[['sepal length','sepal width', 'petal lenth', 'petal width']].values
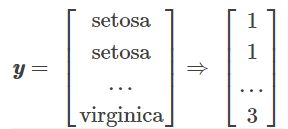
y = df['class label'].values

# 将标签编码
from sklearn.preprocessing import LabelEncoder
enc = LabelEncoder()
label_encoder = enc.fit(y)
y = label_encoder.transform(y) + 1
label_dict = {index+1:label for index,label in enumerate(enc.classes_)}
# label_dict = {1: 'Iris-setosa', 2: 'Iris-versicolor', 3: 'Iris-virginica'}

import numpy as np
np.set_printoptions(precision = 4)

# 分别求三种鸢尾花数据在不同特征维度上的均值向量
mean_vectors = []
for cl in range(1,4):
    mean_vectors.append(np.mean(X[y==cl], axis=0))
    print('Mean Vector class %s: %s' % (cl, mean_vectors[cl - 1]))

Mean Vector class 1: [5.006 3.418 1.464 0.244]
Mean Vector class 2: [5.936 2.77 4.26 1.326]
Mean Vector class 3: [6.588 2.974 5.552 2.026]

二. 计算两个4×4 维矩阵的类内散布矩阵

S_W = np.zeros((4, 4))
for cl,mv in zip(range(1,4), mean_vectors):
    class_sc_mat = np.zeros((4, 4))
    for row in X[y == cl]:
        row,mv = row.reshape(4, 1), mv.reshape(4, 1)
        class_sc_mat += (row - mv).dot((row - mv).T)
    S_W += class_sc_mat
print('Within-class Scatter Matrix:\n', S_W)

三. 计算两个4×4 维矩阵的类间散布矩阵

overall_mean = np.mean(X, axis = 0)

S_B = np.zeros((4,4))
for i,mean_vec in enumerate(mean_vectors):
    n = X[y == i+1, :].shape[0]
    mean_vec = mean_vec.reshape(4, 1)
    overall_mean = overall_mean.reshape(4, 1)
    S_B += n * (mean_vec - overall_mean).dot((mean_vec - overall_mean).T)
print('Between-class Scatter Matrix:\n', S_B)

Between-class Scatter Matrix:
[[ 63.2121 -19.534 165.1647 71.3631]
[-19.534 10.9776 -56.0552 -22.4924]
[165.1647 -56.0552 436.6437 186.9081]
[ 71.3631 -22.4924 186.9081 80.6041]]

四. 求解矩阵特征向量和特征向量

eig_vals,eig_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B)) #特征值,特征向量

for i in range(len(eig_vals)):
    eigvec_sc = eig_vecs[:,i].reshape(4,1)
    print('Eigenvector {}: \n{}'.format(i+1, eigvec_sc.real))
    print('Eigenvalue {}: {:.2e}'.format(i+1, eig_vals[i].real))

• 特征向量：表示映射方向
• 特征值：特征向量的重要程度

eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
eig_pairs = sorted(eig_pairs, key = lambda k:k[0], reverse=True)

for i in eig_pairs:
    print(i[0])

32.27195779972981
0.27756686384003953
1.1483362279322388e-14
3.422458920849769e-15

print('Veriance explained:')
eigv_sum = sum(eig_vals)
for i,j in enumerate(eig_pairs):
    print('eigenvalue {}: {:.2%}'.format(i+1, (j[0] / eigv_sum).real))

Veriance explained:
eigenvalue 1: 99.15%
eigenvalue 2: 0.85%
eigenvalue 3: 0.00%
eigenvalue 4: 0.00%

五. 选择前两维特征

W = np.hstack((eig_pairs[0][1].reshape(4,1), eig_pairs[1][1].reshape(4,1)))
print('Matrix W:\n', W.real)

Matrix W:
[[-0.2049 -0.009 ]
[-0.3871 -0.589 ]
[ 0.5465 0.2543]
[ 0.7138 -0.767 ]]

X_lda = X.dot(W)
assert X_lda.shape == (150,2), 'The matrix is not 150*2 dimensional.'
# assert(断言):判断一个表达式,在表达式条件为false的时候触发异常

import matplotlib.pyplot as plt

def plot_step_lda():
    fig,ax = plt.subplots(figsize = (8, 6))
    for label,marker,color in zip(range(1,4),('^','s','o'),('blue','red','green')):
        plt.scatter(x=X_lda[:,0].real[y==label],y=X_lda[:,1].real[y==label],
                   marker=marker,color=color,alpha=0.5, label=label_dict[label])
    plt.xlabel('LD1', fontsize = 15)
    plt.ylabel('LD2', fontsize = 15)
    
    leg = plt.legend(loc='best', fontsize=14, fancybox=True)
    leg.get_frame().set_alpha(0.5)
    plt.title('LDA: Iris projection onto the first 2 linear discriminants',fontsize=18)
    
    plt.grid()
    plt.tight_layout()
    plt.show()
plot_step_lda()

*sklearn中的LDA模块

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
sklearn_lda = LDA(n_components = 2)
X_lda_sklearn = sklearn_lda.fit_transform(X, y)

def plot_scikit_lda(X, title):
    fig,ax = plt.subplots(figsize=(8,6))
    for label,marker,color in zip(range(1,4),('^','s','o'),('blue','red','green')):
        plt.scatter(x=X[:,0][y==label],y=X[:,1][y==label]*-1,marker=marker,color=color,alpha=0.6,label=label_dict[label])
    plt.xlabel('LD1',fontsize=15)
    plt.ylabel('LD2',fontsize=15)
    
    leg = plt.legend(loc='best', fontsize=14, fancybox=True)
    leg.get_frame().set_alpha(0.5)
    plt.title(title, fontsize=18)
    
#     plt.tick_params(axis='both',which='both',bottom='off',top='off',labelbottom='on',
#                     left='off',right='off',labelleft='on')
#     ax.spines['top'].set_visible(False)
#     ax.spines['bottom'].set_visible(False)
#     ax.spines['left'].set_visible(False)
#     ax.spines['right'].set_visible(False)
    
    plt.grid()
    plt.tight_layout()
    plt.show()
    
plot_scikit_lda(X_lda_sklearn, title='Default LDA via scikit-learn')