Coursea-吴恩达-machine learning学习笔记（十四）【week 8之Dimensionality Reduction】

维数约减又称为降维。
使用维数约减的原因：
1. 数据压缩(减少空间占用，同时为算法提速)
例1：从 2D→1D 2 D → 1 D
存在如下图所示样本集， x(i)∈R2 x ( i ) ∈ R 2

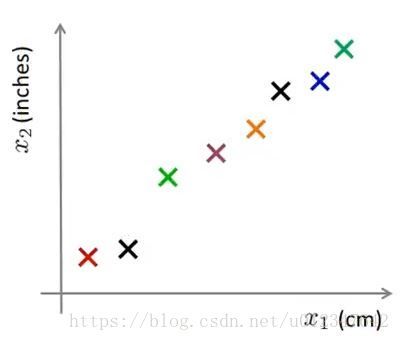
希望找到如下图中所示直线，把所有样本映射到这条线上

如此，就可以使用下图来表示样本位置，只需要一个特征变量即可：

x(1)∈R2→z(1)∈R x ( 1 ) ∈ R 2 → z ( 1 ) ∈ R
x(2)∈R2→z(2)∈R x ( 2 ) ∈ R 2 → z ( 2 ) ∈ R
⋯ ⋯
x(m)∈R2→z(m)∈R x ( m ) ∈ R 2 → z ( m ) ∈ R

例2：从 3D→2D 3 D → 2 D
存在如下图所示样本集， x(i)∈R3 x ( i ) ∈ R 3

把所有样本投影到一个二维平面上，如下图所示：

则可以使用两个特征值来表示样本点的位置，如下图：

z(i)=[z(i)1z(i)2] z ( i ) = [ z 1 ( i ) z 2 ( i ) ]
2. 数据可视化
当 x(i)∈R50 x ( i ) ∈ R 50 时，无法有效观察理解数据，将其降维至 z(i)∈R3 z ( i ) ∈ R 3 或 z(i)∈R2 z ( i ) ∈ R 2 ，就可以呈现为 3D 3 D 或 2D 2 D 的图像。

主成分分析法(PCA)：是当前最常用的降维算法。

PCA实质为寻找一个低维的面，把数据投射在上面，使得样本点到面的垂直距离的平方和达到最小值。这些垂直距离也称为投影误差。
更一般化的表达是：从 n n 维降到 k k 维，找到 k k 个向量 u(1),u(2),⋯,u(k) u ( 1 ) , u ( 2 ) , ⋯ , u ( k ) ，将样本数据投射在这 k k 个向量上，使得投影误差最小。

在应用PCA之前，通常会进行均值归一化和特征规范化。

训练集： {x(1),x(2),⋯,x(m)} { x ( 1 ) , x ( 2 ) , ⋯ , x ( m ) }
在执行PCA算法前的数据预处理：

1. 均值归一化
   μj=1m∑i=1mx(i)j μ j = 1 m ∑ i = 1 m x j ( i )
   用 x(i)j−μj x j ( i ) − μ j 替换 x(i)j x j ( i )
2. 特征缩放(可选)
   如果不同特征值取值范围差异较大，则进行特征缩放，使得各特征值具有类似的取值范围。
   用 x(i)j−μjsj x j ( i ) − μ j s j 替换 x(i)j x j ( i ) ， sj s j 表示特征值 xj x j 的最大值-最小值或标准差。

PCA算法：
将数据从 n n 维降维到 k k 维：
⇒ ⇒ 计算协方差矩阵： Σ=1m∑i=1m(x(i))(x(i))T Σ = 1 m ∑ i = 1 m ( x ( i ) ) ( x ( i ) ) T (注： Σ Σ 表示希腊字母Sigma)
Octave O c t a v e 代码：Sigma=(1/m)*X'*X 其中 X=⎡⎣⎢⎢⎢⎢⎢⎢x(1)Tx(2)T⋮x(m)T⎤⎦⎥⎥⎥⎥⎥⎥ X = [ x ( 1 ) T x ( 2 ) T ⋮ x ( m ) T ]
⇒ ⇒ 计算矩阵 Σ Σ 的特征向量：
Octave O c t a v e 代码：[U,S,V]=svd(Sigma);
svd表示奇异值分解，在 Octave O c t a v e 中，也可以用eig()命令求特征向量；
Sigma协方差矩阵是一个 n×n n × n 矩阵；
上述语句输出三个矩阵，我们需要的是 U U 矩阵，也是 n×n n × n 矩阵；
U U 矩阵的列就是我们需要的向量： U=[u(1),u(2),⋯,u(n)]∈Rn×n U = [ u ( 1 ) , u ( 2 ) , ⋯ , u ( n ) ] ∈ R n × n ；
⇒ ⇒ 提取 U U 矩阵的前 k k 列向量组成矩阵 Ureduce=[u(1),u(2),⋯,u(k)]∈Rn×k U r e d u c e = [ u ( 1 ) , u ( 2 ) , ⋯ , u ( k ) ] ∈ R n × k
Octave O c t a v e 代码：Ureduce=U(:,1:k);
⇒ ⇒ 我们的目的是 x∈Rn→z∈Rk x ∈ R n → z ∈ R k ， z=UreduceTx z = U r e d u c e T x
其中， UreduceT∈Rk×n,x∈Rn×1 U r e d u c e T ∈ R k × n , x ∈ R n × 1 ，所以 z∈Rk z ∈ R k
Octave O c t a v e 代码：z=Ureduce'*x;
注：使用PCA算法， x∈Rn x ∈ R n ，没有 x0=1 x 0 = 1 这一项。

PCA算法压缩数据的原始数据重构：
由上已知： z=UreduceTx z = U r e d u c e T x ，我们现在需要 z∈Rk→x∈Rn z ∈ R k → x ∈ R n
所以： xapprox=Ureducez≈x x a p p r o x = U r e d u c e z ≈ x ， Ureduce U r e d u c e 为 n×k n × k 矩阵， z z 为 k×1 k × 1 向量，故 xapprox x a p p r o x 为 n×1 n × 1 向量。

PCA算法中，把 n n 维特征变量降维到 k k 维特征变量， k k 也被称为主成分的数量。

如何选择 k k ？
两个定义：

平均平方映射误差： 1m∑i=1m∥x(i)−x(i)approx∥2 1 m ∑ i = 1 m ‖ x ( i ) − x a p p r o x ( i ) ‖ 2 ，表示样本 x x 和其在低维平面映射点之间的距离的平方的均值。
数据的总变差： 1m∑i=1m∥x(i)∥2 1 m ∑ i = 1 m ‖ x ( i ) ‖ 2 ，训练样本长度的平方的均值，表示训练样本与 0 0 向量的平均距离。

选择 k k 的法则：
使

1m∑i=1m∥x(i)−x(i)approx∥21m∑i=1m∥x(i)∥2⩽0.01 1 m ∑ i = 1 m ‖ x ( i ) − x a p p r o x ( i ) ‖ 2 1 m ∑ i = 1 m ‖ x ( i ) ‖ 2 ⩽ 0.01

的最小的 k k 值。
此时，保留了 99% 99 % 的差异性。

算法：
⇒ ⇒ 用 k=1 k = 1 尝试PCA算法：
计算 Ureduce,z(1),z(2),⋯,z(m),x(1)approx,⋯,x(m)approx U r e d u c e , z ( 1 ) , z ( 2 ) , ⋯ , z ( m ) , x a p p r o x ( 1 ) , ⋯ , x a p p r o x ( m ) ；
⇒ ⇒ 检查 1m∑i=1m∥x(i)−x(i)approx∥21m∑i=1m∥x(i)∥2 1 m ∑ i = 1 m ‖ x ( i ) − x a p p r o x ( i ) ‖ 2 1 m ∑ i = 1 m ‖ x ( i ) ‖ 2 是否 ⩽0.01 ⩽ 0.01 ；
⇒ ⇒ 若符合条件，取 k=1 k = 1 ，若不符合条件， k++ k + + ，直到找到满足条件的最小的 k k 值。

上述算法的计算过于繁杂，对该算法进行改进。

改进版算法：
⇒ ⇒ 执行语句[U,S,V]=svd(Sigma)会得到 S S 矩阵；
S S 矩阵是一个正方形矩阵，形式为 ⎡⎣⎢⎢⎢⎢⎢S11S22⋱Snn⎤⎦⎥⎥⎥⎥⎥ [ S 11 S 22 ⋱ S n n ]
⇒ ⇒ 对于给定的 k k 值，只需满足 1−∑i=1kSii∑i=1nSii⩽0.01 1 − ∑ i = 1 k S i i ∑ i = 1 n S i i ⩽ 0.01 即 ∑i=1kSii∑i=1nSii⩾0.99 ∑ i = 1 k S i i ∑ i = 1 n S i i ⩾ 0.99
⇒ ⇒ 不断增加 k k 的取值来寻求满足的条件的最小 k k 值。

当使用特定的 k k 值时，也可以用 ∑i=1kSii∑i=1nSii ∑ i = 1 k S i i ∑ i = 1 n S i i 来表示PCA算法性能。

PCA算法应用

⋆ ⋆ 监督学习算法加速
⇒ ⇒ 存在样本集 {(x(1),y(1)),(x(2),y(2)),⋯,(x(m),y(m))} { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( m ) , y ( m ) ) } ；
⇒ ⇒ 提取出输入特征值，无标签数据集 {x(1),x(2),⋯,x(m)}∈R10000 { x ( 1 ) , x ( 2 ) , ⋯ , x ( m ) } ∈ R 10000 ；
⇒ ⇒ 执行PCA算法，得到数据集 {z(1),z(2),⋯,z(m)}∈R1000 { z ( 1 ) , z ( 2 ) , ⋯ , z ( m ) } ∈ R 1000 ；
⇒ ⇒ 形成新的训练样本： {(z(1),y(1)),(z(2),y(2)),⋯,(z(m),y(m))} { ( z ( 1 ) , y ( 1 ) ) , ( z ( 2 ) , y ( 2 ) ) , ⋯ , ( z ( m ) , y ( m ) ) } ；
⇒ ⇒ 提出基于新训练样本的假设函数 hθ(z) h θ ( z ) 。
注： x(i)→z(i) x ( i ) → z ( i ) 的映射关系是通过在训练集上运行PCA算法定义的，这个映射关系同样适用于交叉验证集和测试集的输入特征值。

常见的PCA算法应用：

1. 数据压缩(节约存储空间，算法加速)
   选择 k k 值，保留 x% x % 的差异性。
2. 数据可视化
   k=2 k = 2 或 3 3 。

PCA算法误用

∗ ∗ 避免过拟合
用 z(i) z ( i ) 代替 x(i) x ( i ) 来减少特征数量： n→k n → k ，且 k<n k < n ；
因为特征值越少，似乎越不容易过拟合；
这方法可能会有作用，但并不是好方法，避免过拟合应该用正则化方法。

∗ ∗ 在设计机器学习系统时，直接使用PCA算法
建议：在执行PCA算法前，首先在原始数据 x(i) x ( i ) 上执行相关算法，只有当算法收敛缓慢，占用内存/磁盘空间很大时，再执行PCA算法，使用 z(i) z ( i ) 计算。