深度学习中噪声标签的影响和识别

问题导入

在机器学习领域中，常见的一类工作是使用带标签数据训练神经网络实现分类、回归或其他目的，这种训练模型学习规律的方法一般称之为监督学习。在监督学习中，训练数据所对应的标签质量对于学习效果至关重要。如果学习时使用的标签数据都是错误的，那么不可能训练出有效的预测模型。同时，深度学习使用的神经网络往往结构复杂，为了得到良好的学习效果，对于带标签的训练数据的数量也有较高要求，即常被提到的大数据或海量数据。

矛盾在于：给数据打标签这个工作在很多场景下需要人工实现，海量、高质量标签本身费时费力，在经济上相对昂贵。因此，实际应用中的机器学习问题必须面对噪音标签的影响，即我们拿到的每一个带标签数据集都要假定其中是包含噪声的。进一步，由于样本量很大，对于每一个带标签数据集，我们不可能人工逐个检查并校正标签。

基于上述矛盾现状，在实际工作中必须面对以下两点问题
1. 训练集带标签样本中噪音达到什么水平对于模型预测结果会有致命影响
2. 对于任意给定带标签训练集，如何快速找出可能是噪音的样本
本文接下来将围绕这两点通过实验给出分析

数据、神经网络设计和代码

本文以Tensorflow教程中提及的MNIST问题[1]为数据来源和问题定义。此问题为图像识别问题，图片为手写的0-9字符，每个图片格式为28*28灰度图。训练集数据包括55000张手写数字和标签，验证集包括约10000张图片和标签。通过训练神经网络从而实现当输入一张验证集中的图片后，神经网络能够正确预测这张图片的标签。

对于MNIST问题本身，Tensorflow教程[2]描述的包含2个卷积池化层的CNN网络已经足以实现99%左右的预测精度，因此在本实验中，笔者直接引用Tensorflow官方样例中的CNN网络[3]作为预测模型的神经网络。

本文所有代码可以在笔者的Github项目中获得：https://github.com/wangyaobupt/NoisyLabels

噪声标签对于分类器性能的影响

考虑到MNIST是机器学习领域使用多年的数据库，且在其数据上训练的模型已经得到了较好的结果，由此可以合理推断其标签本身的噪声含量较低（这个推理将在下一个章节通过实验证实）。因此，在这一节的实验中，我们假定原始的MNIST的训练集和验证集标签都是无噪声的。

使用如下步骤给标签添加噪声
1. 根据给定的噪声比例noiseLevel，从N个总样本中选择出K个样本，K = N*noiseLevel
2. 对于选出的K个样本中的每一个样本，将其原始标签替换为0-9之间扣除原始标签之外的随机数

上述算法的代码实现如下，testcase2.py提供了完整的可执行程序

# Add random noise to MNIST training set
# input:
#       mnist_data: data structure that follow tensorflow MNIST demo
#       noise_level: a percentage from 0 to 1, indicate how many percentage of labels are wrong
def addRandomNoiseToTrainingSet(mnist_data, noise_level):
    # the data structure of labels refer to DataSet in tensorflow/tensorflow/contrib/learn/python/learn/datasets/mnist.py 
    label_data_set = mnist_data.train.labels
    #print label_data_set.shape

    totalNum = label_data_set.shape[0]
    corruptedIdxList = randomSelectKFromN(int(noise_level*totalNum),totalNum)
    #print 'DEBUG: 1st elements in corruptedIdxList is: ', corruptedIdxList[0], ' length = ', len(corruptedIdxList)

    for cIdx in corruptedIdxList:
        #print "DEBUG: convert index = ", cIdx
        correctLabel = label_data_set[cIdx]
        #print 'DEBUG: Correct label = ', correctLabel
        wrongLabel = convertCorrectLabelToCorruptedLabel(correctLabel)
        #print 'DEBUG: Wrong label = ', wrongLabel
        label_data_set[cIdx] = wrongLabel


# uniform randomly select K integers from range [0,N-1]
def randomSelectKFromN(K, N):
    #print 'DEBUG: K = ',K, ' N = ', N
    resultList =[]
    seqList = range(N)
    while (len(resultList) < K):
        index = (int)(np.random.rand(1)[0] * len(seqList))
        #index = 0 # for DEBUG ONLY
        resultList.append(seqList[index])
        seqList.remove(seqList[index])
    #print resultList
    return resultList

# Convert correct ont-hot vector label to a wrong label, the error pattern is randomly selected, i.e. not considering the content of image
def convertCorrectLabelToCorruptedLabel(correctLabel):
    correct_value = np.argmax(correctLabel, 0)
    target_value = int(np.random.rand(1)[0]*10)%10
    if target_value == correct_value:
        target_value = ((target_value+1) % 10)
    result = np.zeros(correctLabel.shape)
    result[target_value] = 1.0 
    return result

这样，当给定噪声水平之后，上述算法完成添加噪声，进一步用带噪声的训练集训练出模型，最终在验证集上对模型评价精度。下图是噪声标签比例在0-100%范围内变化时，模型精度的变化。

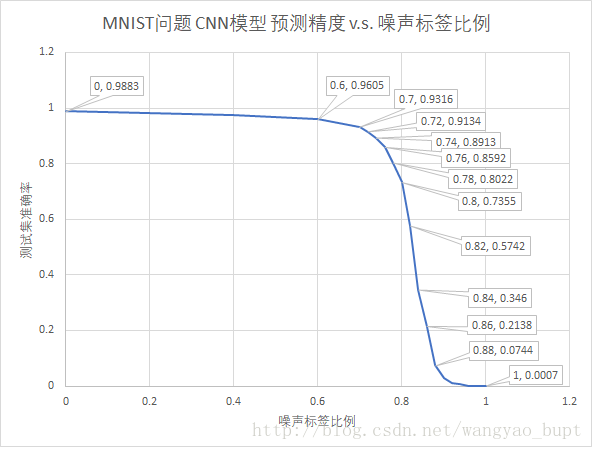
从上图可以看出，在噪声标签占比不超过60%的情况下，验证集精度保持在96%以上，即便噪声标签占比达到70%，验证集精度仍然能达到93%。在噪声标签占比超过70%之后，精度结果快速下降，当噪声占比达到88%时，预测精度已经下降到7%。这个水平已经低于纯随机预测，考虑到此问题为10分类问题，在完全随机的情况下，预期精度的数学期望也在10%左右。

这里就引出了两个问题：
1. 为什么在噪音标签占比70%的情况下，模型抗噪声性能这么好？
2. 70%之后的快速下降又是由什么导致的

为了回答上述问题，要重新审视此前加噪声标签的方法。在加噪声的第一步，我们均匀的随机抽取出一定比例的标签，考虑到原始数据10类标签的分布是基本均匀的，那么抽出来的K个样本中10类标签的数量基本一致。在第二步，对于每个标签，我们将正确标签抹去，从正确标签之外的9个字符中选择一个作为标签，由于选择算法本身也是随机的，那么，错误标签是均匀分布在其他9类的。
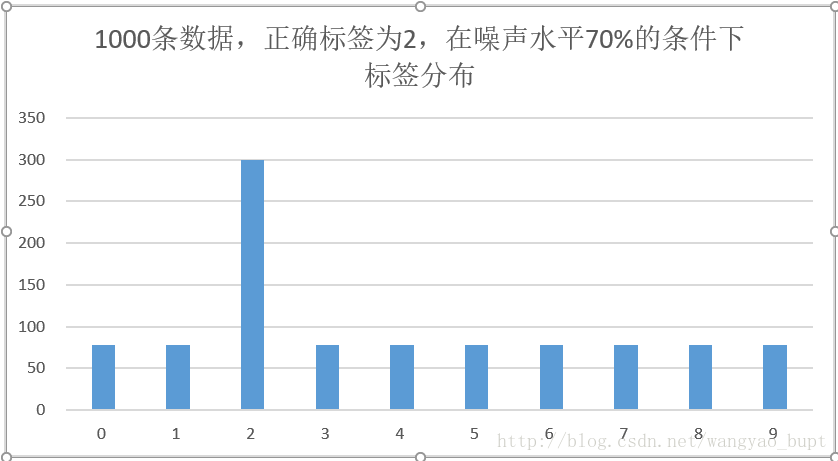
上述解释如果还不够直观，那么可以看下图。假设有1000条正确标签为2的数据，在70%的噪声条件下，只有300条数据标签为2，其余700条数据的标签均匀分布在其他9类。这样，正确标签（300条‘2’标签）相比其他任何一个类别，仍然占有明显数量优势，所以CNN才可以根据这个数量优势学习到正确标签2.

而当噪声比例进一步增加后，数量对比优势会逐渐弱化，例如下图。这种情况下正确标签虽然占比仍然多于其他分类，但是数量上已经只有2倍的差异。在模型训练中，正确标签带来的梯度下降增益不足以对抗错误标签的影响，神经网络倾向于学习到随机标签。

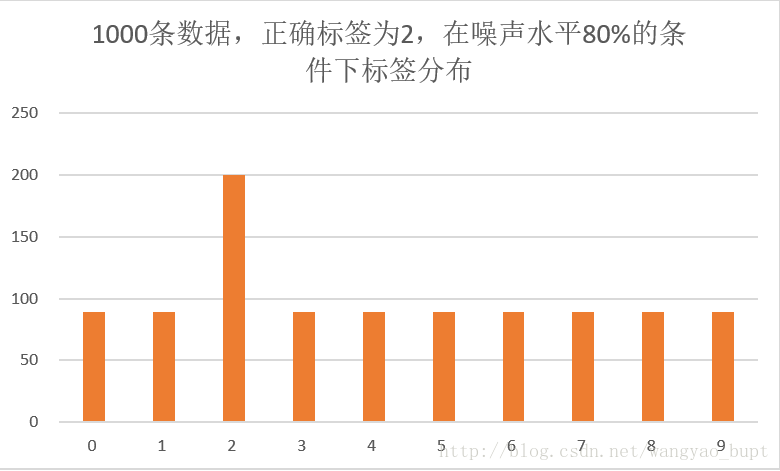
由上述两张图可以看出，如果在多分类问题中噪音标签是均匀分布的，同时正确标签相对于每个类别的错误标签有数倍的数量优势，那么训练过程有可能承受较高的噪声标签水平得到相对精确的模型。但如果噪音标签已经与正确标签数量接近，那么很难训练出有意义的模型。

如何快速识别出疑似噪声的标签

在真实应用中，我们显然不会人工在训练数据集上添加噪声。但如前文所述，训练数据集本身是含有噪声的，除了人工逐个审查，有没有办法快速找出疑似是噪声的标签呢？

为了解决这个问题，我们回到基于CNN网络的MNIST分类器最后一层来看。在分类器的最后一层，全连接网络包含10个神经元，输出10个运算结果，可以看作一个10维向量。这个10维向量经过softmax运算可以转为离散概率分布，其和为1，每个维度代表分类器预测当前图片属于某一类的概率。最终的预测结果就是取离散概率分布中概率值最高的一类作为预测结果。

在实验中观察不同样本的概率分布，可以看到有以下两种情况

• 当一张图片清晰且无歧义时，神经网络输出的离散概率分布是集中在一个标签的，例如正确标签概率为0.999，其余9种类别的概率接近于0.
  当一张图片存在歧义时，神经网络输出的离散概率分布就不会只集中在一个标签，有可能最强的标签概率只有0.6，第二强的标签概率0.39，其余8个类别概率为0
  这样的结果意味着神经网络认为这张标签有二义性。

基于这个认识，就可以设计出一种方法，让神经网络把自己认为存在二义性的样本和标签筛选出来，即实现了非人工快速找出疑似噪音标签。

下面是二义性判断的代码实现，二义性在这里定量的定义为：分类器认为最有可能类别的概率低于70%，同时第二可能类别概率高于15%。下列代码是挑选二义性概率分布的实现，是simpleCNN.py的一部分，testcase3.py提供了筛选二义性样本的可执行程序

    # Filter out images with low SNR.
    # The term 'low SNR' is defined as: in the probability distribution of this sample, the largest value is <= 0.7, while the 2nd largest value >= 0.15
    # the raw images data (in shape of 1*784 vector), labels, and top 2 possibilities by CNN will be returned
    # Parameter:
    # train_or_test, 0 means train data, 1 means test data
    def filterLowSNRSamples(self, mnist, train_or_test=0):
        if train_or_test == 1:
            data = mnist.test
        else:
            data = mnist.train

        resultList = []

        for sample_idx in range(data.images.shape[0]):
            prob_dist, label=self.sess.run([self.output_prob_distribution, self.label], feed_dict={
                    self.x: np.reshape(data.images[sample_idx], (1, 784)), self.y_: np.reshape(data.labels[sample_idx], (1,10)), self.keep_prob:1.0})

            raw_prob_array = prob_dist[0]

            #search for position of the largest value and the 2nd largest value
            top_1_pos , top_2_pos = findPosOfLargestTwoElement(raw_prob_array, 10)

            #Low SNR criteria
            if raw_prob_array[top_1_pos] <= 0.7 and raw_prob_array[top_2_pos] >= 0.15:
                resultList.append((sample_idx, data.images[sample_idx], label, top_1_pos, top_2_pos))

            if (sample_idx % 1000 == 0):
                print "DEBUG, current idx = %d, num_of_low_SNR = %d" % (sample_idx, len(resultList))
        return resultList

使用这套方法，在MNIST的55000个训练数据和标签中筛选出408个疑似有二义性的图片，下图是部分典型图片。由此来看，MNIST本身的标签质量是较高的。下图中不少标签人工识别也存在困难，这恰恰说明了找出的标签很大程度上就是“疑似噪声标签”

小结

本文对于MNIST数据集，使用CNN分类器，考察了噪声对模型预测精度的影响，实验结果表明，在均匀分布的随机噪声条件下，CNN模型可以在噪声标签占比70%的情况下预测精度无明显下降。进一步，为了识别原始训练集中的疑似噪声样本，文中使用训练好的CNN模型通过预测向量的概率分布，识别存在二义性的标签，实现了低代价找出训练集噪声标签的目的。

参考文献
[1] https://www.tensorflow.org/get_started/mnist/beginners
[2] https://www.tensorflow.org/get_started/mnist/pros
[3] https://github.com/tensorflow/tensorflow/tree/master/tensorflow/examples/tutorials/mnist