基于图正则化稀疏判别分析的人脸识别

基于图正则化稀疏判别分析的人脸识别

 

摘要

流形学习和稀疏表示的分类技术是人脸识别的两种流行的技术。因为流形学习能用低维表示高维数据，广泛应用于计算机视觉和模式识别。大多数流形学习算法可以嵌入框架，第一步是确定相邻图。传统的方法是采用k近邻或k-球模型。然而，它们是参数化的并且对噪声敏感。此外，很难确定适当邻域的大小。为了解决这些问题，在本文中提出了正则化稀疏图判别分析，grsda等方法。基于图嵌入和保稀疏投影的内禀权矩阵。通过稀疏表示得到惩罚图。grsda寻求子空间的类内样本尽可能紧凑，而类间的样本可能是可分离的。具体fi卡利，在低维空间中的样本可以保留稀疏的地方的关系在同一类中，同时提高不同类样本的可分性。因此，grsda可以获得更好的性能。大量的实验在ORL，耶鲁-B和AR人脸数据库上进行，结果表明本文提出的算法优于fiLPP，UDP，SPP和dsnpe。

 

1.介绍

人脸识别作为模式识别的一个流行的应用—在研究领域中计算机视觉技术引起了人们极大的兴趣。人脸识别的主要步骤包括预处理，特征提取和分类。为了使后面的任务轻松一些，已经对预处理提出了许多算法，并且还有一份关于人脸识别的报告。人脸识别的分类是从简单的最近邻（NN）[ 4 ]发展而来，最近提出的基于回归的分类算法的方法,一些如线性回归分类fiER（LRC）[ 5 ]，SRC[6]和CRC[7]。这三种基于回归的算法均取得了类似的结果，他们在实际应用中均表现出了巨大的潜力。此外，在[ 8-10 ]也提出了许多上述分类算法。除了这些，支持向量机（SVM）[ 11 ]和深度学习[12,13]在人脸识别中也很常用。例如，当深度学习应用于人脸识别时，一种叫做DeepFace [ 12 ]的算法在标记的数据集中能取得较好的结果。

在所有的人脸识别算法中，基于外观的子空间学习方法因其简单和理想的性能引起了极大的关注。因为人脸图像的维度通常很高，降维也称做特征提取，是人脸识别中的关键问题。在过去的20年中受到了极大的关注。计算机视觉和模式识别中的许多应用如人脸识别、基于内容的图像检索、生物信息学等经常面临采取的样品为高维和非线性。然而，本文给出了一个有效降维的方法[14]。在过去的几十年中已经提出很多算法，其中有两个广泛使用的是主成分分析（PCA）[ 15 ]和线性判别分析（LDA）[16,17]，这两者均有矩阵—分解为基础的方法[ 18 ]，并假设DIS—样品是全局线性分布。然而，在许多应用中例如考虑高维数据的人脸图像，样品的分布通常是非线性的。可以通过使用内核技巧来处理这个问题，将之前空间的原始数据映射到一个更高的维度空间。在内核空间数据被假定为线性可分的。内核空间的数据被假定为线性可分的。核主成分分析（KPCA）[ 19 ]和核线性鉴别分析（KLDA）[ 20 ]在模式识别中代表有效性。然而，如何选择合适的内核是最关键的问题，因为它经常影响算法。

另一类是流形学习算法（例如，Isomap [ 21 ]，局部线性嵌入（LLE）[ 22 ]，Laplacian嵌入（LE）[ 23 ]，局部切空间排列（LTSA）[ 24 ]，平行向量场嵌入（PFE）[ 25 ]，测地距离函数学习（GDL）[ 26 ]，并现场校准跨媒体检索（施肥）[ 27 ]），已提出发现内在的低维可以表示高维和非线性数据。然而，这类算法不能匹配一种新的样品到相应的低维量纲空间，也称为样本推广问题[ 28 ]。因此针对这个问题提出了很多方法，可以实现显式映射，如局部保持投影（LPP）[ 29,30 ]，邻居保持嵌入（NPE）[ 31 ]，无病鉴别投影（UDP）[ 32 ]，边际Fisher分析（MFA）[ 33 ]，线性判别嵌入（LDE）[ 34 ]，正交LPP[ 35 ]，局部保持判别投影（LPDP）[ 36 ]，判别式多流形分析[ 37 ]和基于特征线距离的迭代子空间分析[ 38 ]。这些算法用一种或另外一种方式考虑了流形结构或判别信息，并表现出比传统方法在一些特殊的场景中更加高效。例如，在[ 37 ]中已经定义了流形图和内管图，再根据标签信息选取了最优投影，取得了良好的结果。并且每个人都只有一个样品。

所有这些方法都可以在图形嵌入框架[39,40]。在这个框架的第一步是建立图，即内图和罚图。然而，这个算法的性能在很大程度上取决于如何构造图。传统方案采用k邻接点法或者ε球球法，但如何选择合适的方法以及邻域大小或球半径仍不清楚。再者对于这两种方法，图的构造和权重分配是独立的。目前还没有一个理想的模型，而且还不能一步完成图结构、权重分配等问题[41]。

最近几年稀疏表示[ 6,42 ]引起了广泛关注。主要方法是给定的测试样本可以表示为训练的线性组合。样本和分类通过评估来实现，该评估会导致最小重建偏差。稀疏表示得到的系数能够建立样本和重建测试样本。据报道[ 43 ]称这些具有大系数的样品可能属于同一类。因此，重建系数可以作为测量类的一种方式。

出于以上考虑，一些研究人员试图用非参数方法构造相邻图，其中图的构建和权重分配可以一步就完成，并且这一技术已被广泛应用。因为应用程序无参数和健壮。颜等人[44,45]提出L1图进行图像分析，并用稀疏矩阵表示构造图。在[ 46 ]图中提出了正则化稀疏编码方法。局部流形结构在稀疏表示中的应用，然而该法性能欠佳。与L1图相似，乔等人[ 47 ]提出稀疏性—服务投影（SPP），其中每一个样本都呈现为剩余样本的线性组合。

SPP试图找到一种能够保持稀疏重构关系的工程。不需要选择邻域参数、尺寸，作者指出它具有天然的辨别力。在一定程度上对噪声具有鲁棒性。然而，SPP作为整个训练集的字典，这是一种非监督类的方法。张等人[ 48 ]介绍了对图的优化稀疏约束降维方法（godrsc），该法试图采纳的稀疏表示系数和嵌入。在[ 49 ]稀疏表示分类转向判别投影（SRC—DP）中，试图和投影的最大化类间重建误差最小化。因此它更优一点。但它忽略了由于投影矩阵和稀疏系统而使得流形结构和时间开销较大。陈和靳[ 50 ]从线性的角度提出了一种新的特征提取方法，称为侦察—结构判别分析（RDA）。桂等人[ 51 ]设计了一个新方案称为判别稀疏邻域保持嵌入（dsnpe），代表数据的一个线性组合，来自同一类的样本并保留了稀疏在同一类的性关系。然而，它忽略了训练样本固有的流形结构，特别是类间流形结构，因为它只集成SPP和max—最佳边缘准则（MMC）[ 52 ]。类似的作品也可以在53,54 [发现]。

利用流形学习的优点和鲁棒性稀疏表示，本文提出了一种新的算法叫做正则化稀疏判别分析（grsda），这利用稀疏表示作为图形构造的一种权重分配的方法。在GRSDA中，内在和惩罚图通过稀疏矩阵表示构造，随后可获得权重，因此避免了确定邻域大小的困难。一方面，它继承了流形结构像LPP；另一方面，它来自判别能力强的LDA。在图形嵌入式框架下，grsda寻求一个同一类的样本尽可能地紧凑的空间，来自不同类的样本尽可能地可分离。

本文的其余部分安排如下：第2节介绍了相关的作品像稀疏表示的概述，保稀疏投影与图嵌入。在第三章提出了图形稀疏判别分析。算法及相关实验结果见第4节。第5节给出结论。

2.相关工作

假设有一个n个样本的训练集，其中D表示维数。共有C个类，在第k类中有n k 个样本（＝1, 2）。降维是为了寻找一个投影，使得在原有空间里能够和低维空间相互匹配。

2.1.稀疏表示

如果给定的测试样本Y属于第i类，稀疏表示假设Y可以表示为第i类训练样本的线性组合。换句话说，我们可以如下所示：如果一个给定的测试样本Y属于第i类，稀疏表示假设Y可以表示为一个第i类的线性组合。换句话说，我们可以表示为如下所示：

 

其中表示y在上的表示系数。理想的情况是。如果把Xi, 1, 2, , i C 放到整个训练集中，那么y可以表示成整个训练集的线性组合， 因此可以得到代表系数矩阵。换句话说也就是：

上述模型可以表示如下：

 

在是的范数，这表示向量W的非零项的数目。

上述优化问题在多项式中不能解决，因为L0范数的优化问题是一个NP问题。幸运的是，最近已经做了很多关于压缩传感[ 55 ]的工作并且表明如果足够稀疏的话那么L0范数等价于L1范数的优化问题。均可以通过下面的优化问题来解决，即：

 

   在获得最优稀疏表示后，可以计算出测试样本和第i类样本之间的重建误差。

 

  　然后标签Y被确定为最小重建误差的类：

 

2.2.稀疏保留投影

 

稀疏保留投影的目的是保存稀疏重构关系，其目标函数是：

其中A是转换矩阵，而I是一个确定的矩阵。此外，是X轴上的稀疏重建系数，它可以通过以下优化问题得到。

 

 

假设X代表整个训练集包括。因此，设。然而，上述优化问题是非凸的。

作者[ 56 ]指出如果足够稀疏，那么范数可以近似解决范数，所以（8）大致相当于下面的优化问题，可用线性规划来解决。

如果计算对每一个(i=1, 2，=⋯N)计算对应的权重向量，我们可以得到稀疏重建权值矩阵，[47]中可以查阅更多细节。

简单代数（7）可以简化为以下问题：

 

2.3.图的嵌入

图的嵌入试图在低维空间中保留当地的相邻关系。样品和它们之间的关系表示为一个图G =（X，W），其中顶点X是由（i= 1, 2…），W是邻接矩阵，表示xi和xj之间的相似性。它的目标函数是:

 

通过简单的代数（11）可以降维到以下问题：

 

   其中D是对角矩阵，，L=D-W是拉普拉斯矩阵。

3.图正则化稀疏判别分析

3.1提出算法

图的嵌入是一种有代表性的流形学习算法，LDA、LPP、UPD和MFA可以在图形嵌入框架实现统一。图的嵌入的第一步是图的构建，而大多采用的方法是K近邻和ε球法。然而，这两种方法都是参数化的，算法的性能依赖于参数值的选择。[ 47 ]据报道表明，邻接图结构图权是相关的，而不应该分开处理。因此，理想的是设计一个一步能同时执行这两项任务的方法。在本节中，我们提出了一个新的方法称为正则化稀疏图的判别分析，通过稀疏表示采用类内和类间的判别信息成图的结构 ，并且计算类内邻接矩阵w和类间邻接矩阵b。

类内图中可以反映xi和xj之间的相似性。越大，xi和xj属于同一个类的几率也就越大。在稀疏表示中，每个样品可表示为其余样品的线性组合的系数，系数表示对的重建。在[6]中，同一类中样品可以相互之间进行有效的重建。因此，可以表示为来自同一个类的样本线性组合。

 

  表示第i类的第j个样本并且Xi表示第i类中除了的样本。通过方程13可以对求出重建系统，并且可以写入作为向量：

     同样地可以以的方式找到第i类的空闲代表系数。此外，对于所有的样本，可以找到类内权重矩阵如下：

 

类似于图的嵌入，本文希望在低维度—三维空间的同一类样本能够尽可能的紧凑。因此建立固有图 ，目标函数为：

可以简化为：

 

是拉普拉斯矩阵，是对角阵，并且有。

另一方面，每个样本都可以表示为来自不同类的样本的线性组合。即

[16]中表示第i类中的第j个样本并且用表示第i类的样本。即：。并且可以得到最优稀疏重构向量如下所示：

 

根据标签信息，可以重写在里面的表现形式。与类间权重矩阵类似，可以得到第i类间权重向量。随后我们可以得到。整个训练集的班级间矩阵为：

 

 

 

中的表示对的重建。的值越大，与越相似。然而他们属于不同的类。定义了不相似矩阵B，由 确定。本文期望在低维空间中，来自不同类的样本尽可能分离。构建有，目标函数为：

或者是简化形式:

 

 

 

    是拉普拉斯矩阵，并且是对角矩阵，并且有D。

类似于边际Fisher分析，通过组合（15）和（18），可得到以下优化问题：

 

 

上述优化问题可以通过以下广义特征问题来解决：

 

 

称作类间稀疏散射矩阵，称作类内稀疏散射矩阵。 假设，并且d是20个特征值里面最大的。对应的特征向量是，可得到投影矩阵。 因此，任何原始空间都可以通过映射到低维空间。

在应用中，如面部识别，空间数量远大于人脸内部的数量，比如稀疏散射矩阵通常是单数。 做内部类稀疏散射矩阵非奇异，主成分分析（PCA），可以保留98％的图像能量。

GRSDA的算法程序可以正式地总结为如下：

输入：训练集为如下：

第k类的尺度为并且  ，固有维数为d。

输出：矩阵A。

步骤1：对于X，预处理过程中PCA保留了图像能量的98％。 为了简化，仍然将X表示为PCA后的训练集。

步骤2：对于X中的每个样本，通过（13）和（16）计算其稀疏代表。 并构建和。为了符合一致性，通过W和B ，由公式和可求。

步骤3：通过和分别计算类内稀疏散射矩阵和类间稀疏散射矩阵。

步骤4：解决（20）中的广义特征值问题，得到d最大的8个特征值和相应的特征向量。结果最后可以获得相应的投影矩阵。

步骤5：对于每个原来空间的样本，低维代表是。

3.2.连接到LDA和LP

LPP尝试保留样本的本地结构。换句话说，如果其他两个样本在原始空间接近，那么它们也在低维空间中是彼此靠近的。但是，LPP的性能严重依赖于相邻的权重。不同的图形将使得LPP产生不同变量。算法是LPP的扩展形式，其中通过稀疏可以计算出相邻权重。

内在图。与使用k最近的常规LPP不同通过邻居法或ε-ball方法来确定邻域大小，提出的方法是无参的。 GRSDA可以通过修改的常规版本作为LPP的正规版本，对现有知识进行编码。

然而LDA试图找出最大化类分散并最小化同步散射的同时，所提出的算法试图找出稀疏散射时选取的轴，对于类间的最大化和类与类之间的稀疏分散是最小化。很明显，LDA和GRSDA之间的区别是散点矩阵的定义不同。

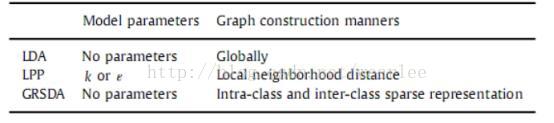
实际上，LDA和LPP可以在图形嵌入中统一框架。 GRSDA是LDA和LPP的一种变体。比较它们模型参数条款和构建图的方式后，表1给出了它们之间的差异。

4.实验和分析

为了评估所提算法的有效性和正确性，对ORL [57]，扩展YALE-B [58]和AR [59]数据库进行了实验，并且将结果与LPP，UDP，SPP和DSNPE进行了比较。

采用LPP，UDP，SPP，DSNPE和GRSDA来查找低维表示，最近邻分类器用于投影空间中的分类。 为了使一些矩阵非奇异，使用PCA作为预处理步骤，并且保留了图像的能量的98％。 对于LPP和UDP，需要确定邻域大小。 在本文中，邻域大小设置为k = - ni 1，其中ni是第i类中的样本数。

4.1.ORL数据库的实验结果

 ORL数据库包含40个人; 每个都有10个图像，10个图像中的姿势，面部表情和一些细节都有一些变化。 每个图像都是在不同的时间拍摄，具有不同的变化，包括像睁开或闭合的眼睛，微笑或不笑的表情。被捕获的一些图像可以容忍一些面部的倾斜和旋转高达20°。图1显示了ORL数据库中的一些样本。

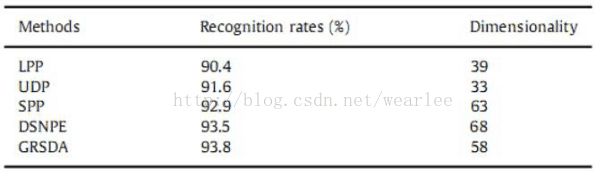
对于ORL数据库，每个图像的大小调整为32×32。 本文随机选择每个受试者的4张图像，形成一个训练集，并将数据库的剩余图像作为一个测试集。对每个算法重复20次，并将这20次中的最佳识别率用作识别率。 表2显示了具有相应维度的每个算法的最佳识别率。

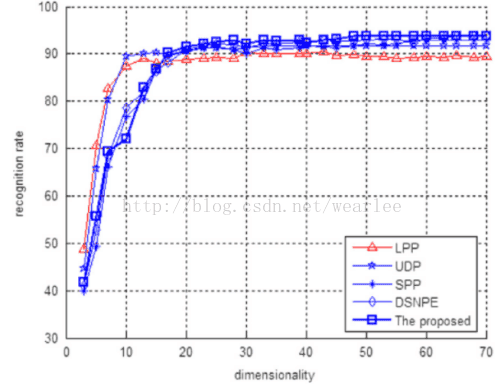
为了评估维度对识别率的影响， 图2示出了针对不同维度的不同方法的识别率。

4.2.扩展YALE-B数据库的实验结果

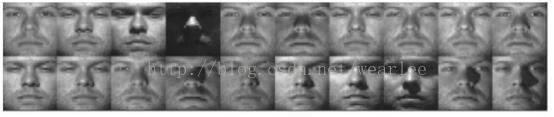
扩展的YALE-B数据库包括38个人，每个人有64个图像，分别在不同的姿势和亮度下被捕获。图3显示了YALE-B数据库中的一些样本。

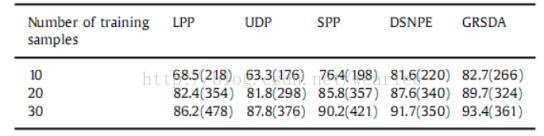
在我们的实验中，为了有效的计算，每个图像被调整为32×32。 我们首先随机选择每个受试者的10,20和30张图像，形成一个训练集，并将数据库的剩余图像作为一个测试集。 我们对每个算法重复20次，并将这20次中的最佳识别率用作识别率。 表3显示了每个算法的最佳识别率（％），相应的维度在括号中给出。

 

 

表1  用LDA、LPP以及GRSDA的图形比较

 

 

表2  在ORL数据库中使用不同的方法情况下对应的是识别速率

 

 

 

 

图1  来自ORL数据库中的图像

 

4.2.AR数据库的实验结果

    AR数据库包含126名受试者（70名男子和56名女性）。有超过4000种颜色的脸部图像，包括面部的正面视图，它们在不同的条件下的两个会话中进行，如不同的面部表情，照明条件和遮挡（太阳镜和围巾）。在我们的实验中，我们选择了100名受试者（50名男性和50名女性）的子集，每组有14个不同的图像。因此，脸部图像的总数为1400。原始图像尺寸为165×120，但为了有效的计算，我们手动将图像大小调整为50×40。图4显示了AR数据库中的一些样本。

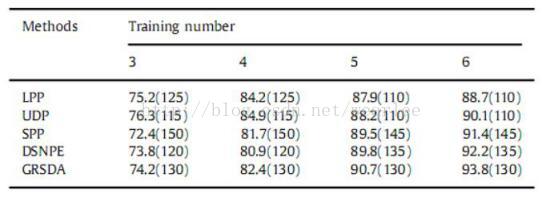
在我们的实验中，我们首先随机选择每个受试者的l（l=  3：4：5：6）图像以形成训练集，并且将数据库的剩余图像作为形成测试集。对于每个l，我们对每个算法重复20次，并将这20次中的最佳识别率用作识别率。表4显示了每个算法的最佳识别率（％），对应的维度在括号中给出。

4.4计算时间

    为了评估计算效率，我们给出了不同方法的计算时间。 计算时间由维数降低和分类的整个操作时间表示。 我们的实验环境是Intel CPU 2.10 GHz，1G RAM内存，MATLAB 7.0.1（R14）。 表5显示了ORL数据库中所有使用的方法对于每个人4个训练样本的计算时间。

从表5的结果可以看出，LPP和UPD比基于稀疏表示的特征提取算法（SPP，DSNPE和GRSDA）要快得多。 这可能是因为SPP，DSNPE和GRSDA涉及l1规范优化问题，这是非常耗时的。

 

图2  识别速率和在ORL数据库中的维度

 表3  在YALE-B数据库中使用不同方法对应的识别速率

 

 

 

图3  来自YALE-B的样本

 

表4  对AR数据库中使用不同方法的识别速率

 

 

表5  在ORL数据库中的对比

 

 

4.5.讨论

从实验中可以看出，所有算法的训练次数越多，效果就越好，如果有更多的训练样本，则提取的特征可以更好地代表样本。我们还可以看到所有的算法在ORL上表现都比其他数据库更好。这可能是因为ORL上的图像变化比YALE-B和AR上的图像小。UDP优于LPP，这可能是因为LPP仅考虑本地结构，而UDP完全利用本地和非本地数据结构。 SPP基于稀疏表示，保留数据的稀疏重建关系。 由于重建系数可以被看作是相似度的测量，也就是说，如果一个样本重建另一个样本的系数较大，则它们更可能来自同一个类。因此，在投影之后，来自同一类的样本被聚集到一定程度上，并且提取的特征包括自然判别信息，即使它是无监督的。DSNPE可以保持同一类中的稀疏重建关系，并最大化不同类之间的边距，因此具有比SPP更好的性能。所提出的算法一方面保留类LPP之间的类内稀疏局部关系，另一方面，最大化了类之间的稀疏分散。所以在投影之后，来自同一类的样本是紧凑的，而来自不同类的样本相差很远。总体而言，提出的算法具有比LPP，UDP，SPP和DSNPE更好的识别性能。

5.结论

在本文中，提出了一种称为图形正则化稀疏判别分析的新的面部识别算法。 基于稀疏保留投影，内在和惩罚图的权重通过稀疏表示获得。该方案避免了为歧管学习算法选择正确的参数的困难，并且图形构造和权重计算在一个步骤内完成。 然后，通过最大化类间稀疏散射，同时最小化类内稀疏散射，在低维空间中，来自同一类的样本是紧凑的，而来自不同类的样本相差很远。 最后，对人脸识别进行实验，结果证实，与相关算法相比，所提出的算法性能优越。 此外，提出的方法表明，当训练数量小时，其性能不好。 我们将在未来的工作中研究这个问题。

致谢

作者要感谢所有匿名评审人员的宝贵建设性言论，对提高本文的质量非常有帮助。 这项工作得到浙江省自然科学基金（No LQ15F020001）和浙江省自然科学基金（No LQ15F020001）和国家自然科学基金（授权号61272261和61203257）的支持。

 

 参考文献

 

[1] Y. Pang, H. Yan, Y. Yuan, K. Wang, Robust CoHOG feature extraction in human-

centered image/video management system, IEEE Trans. Syst. Man Cybern. Part

B: Cybern. 42 (2) (2012) 458–468.

[2] X. Jiang, Y. Pang, J. Pan, X. Li, Flexible sliding windows with adaptive pixel

strides, Signal Process. 110 (2015) 37–45.

[3] E. Hjelmås, B.K. Low, Face detection: a survey, Comput. Vis. Image Underst. 83

(3) (2001) 236–274.

[4] T. Cover, P. Hart, Nearest neighbor pattern classification, IEEE Trans. Inf. Theory

13 (1) (1967) 21–27.

[5] I. Naseem, R. Togneri, M. Bennamoun, Linear regression for face recognition,

IEEE Trans. Pattern Anal. Mach. Intell. 32 (11) (2010) 2106–2112.

[6] J. Wright, A. Yang, A. Ganesh, S. Sastry, Y. Ma, Robust face recognition via

sparse representation, IEEE Trans. Pattern Anal. Mach. Intell. 31 (2) (2009)

210–227.

[7] L. Zhang, M. Yang, X. Feng, Sparse representation or collaborative repre-

sentation: which helps face recognition?, in: Proceedings of ICCV, 2011, pp.

471–478.

[8] Y. Xu, D. Zhang, J. Yang, J.-Y. Yang, A two-phase test sample sparse repre-

sentation method for use with face recognition, IEEE Trans. Circuits Syst. Video

Technol. 21 (9) (2011) 255–1262.

[9] Allen Y. Yang, et al., Fast-minimization algorithms for robust face recognition,

IEEE Trans. Image Process. 22 (8) (2013) 3234–3246.

[10] A.Wagner, J. Wright, A. Ganesh, Z. Zhou, H. Mobahi, Y. Ma, Towards a practical

face recognition system: robust alignment and illumination by sparse repre-

sentation, IEEE Trans. Pattern Anal. Mach. Intell. 34 (2) (2012) 372–386.

[11] Y. Pang, K. Zhang, Y. Yuan, K. Wang, Distributed object detection with linear

SVMs, IEEE Trans. Cybern. 44 (11) (2014) 2122–2133.

[12] Y. Taigman, Ming Yang, M. Ranzato, L. Wolf, DeepFace: closing the gap to

human-level performance in face verification, in: Proc. IEEE Conf. Comput. Vis.

Pattern Recognit., 2014, pp. 1701–1708.

[13] Y. Sun, Y. Chen, X. Wang, Deep learning face representation by joint identifi-

cation–verification, Adv. Neural Inf. Process. Syst. (2014) 1988–1996.

[14] A.K. Jain, R.P.W. Duin, J. Mao, Statistical pattern recognition: a review, IEEE

Trans. Pattern Anal. Mach. Intell. 22 (1) (2000) 4–37.

[15] H. Abdi., L.J. Williams, Principal component analysis, Wiley Interdiscip. Rev.:

Comput. Stat. 2 (4) (2010) 433–459.

[16] A. Martinez, A. Kak, PCA versus LDA, IEEE Trans. Pattern Anal. Mach. Intell. 23

(2) (2001) 228–233.

[17] Y. Pang, S. Wang, Y. Yuan, Learning regularized LDA by clustering, IEEE Trans.

Neural Netw. Learn. Syst. 25 (12) (2014) 2191–2201.

[18] X. Li, Y. Pang, Deterministic column-based matrix decomposition, IEEE Trans.

Knowl. Data Eng. 22 (1) (2010) 145–149.

[19] Bernhard Scholkopf, Alexander Smola, Klaus-Robert Muller, Nonlinear com-

ponent analysis as a kernel eigenvalue problem, Neural Comput. 10 (5) (1998)

1299–1319.

[20] S. Mika, G. Ratsch, J. Weston, B. Scholkopf, Fisher discriminant analysis with

kernels, in: Proceedings of the IEEE Signal Processing Society Workshop on

Neural Network for Signal Processing, 1999, pp. 41–48.

[21] J.B. Tenenbaum, V. Silva, J.C. de, Langford, A global geometric framework for

nonlinear dimensionality reduction, Science 290 (2000) 2319–2323.

[22] S. Rowies, L. Saul, Nonlinear dimensionality reduction by locally linear

embedding, Science 290 (2000) 2323–2326.

[23] M. Belkin, P. Niyogo, Laplacian eigenmaps for dimensionality reduction and

data representation, Neural Comput. 15 (6) (2003) 1373–1396.

[24] Zhenyue Zhang, Hongyuan Zha, Principal manifolds and nonlinear dimension

reduction via local tangent space alignment, SIAM J. Sci. Comput. 26 (1) (2004)

[25] B. Lin, X. He, C. Zhang, Ming Ji, Parallel vector field embedding, J. Mach. Learn.

Res. 14 (1) (2013) 2945–2977.

[26] B. Lin, J. Yang, X. He, J. Ye, Geodesic distance function learning via heat flow on

vector fields, in: Proceedings of ICML, 2014, pp. 145–153.

[27] X. Mao, B. Lin, D. Cai, X. He, J. Pei, Parallel field alignment for cross media

retrieval, in: Proceedings of ACM Multimedia, 2013, pp. 897–906.

[28] F. Dornaika, B. Raducanu, Out-of-Sample embedding for manifold learning

applied to face recognition, in: Proceedings of CVPR, 2013, pp. 862–868.13–338.

[29] X. He, P. Niyogi, J. Han, Face recognition using Laplacian faces, IEEE Trans.

Pattern Anal. Mach. Intell. 27 (3) (2005) 328–340.

[30] Y. Xu, A. Zhong, J. Yang, D. Zhang, LPP solution schemes for use with face

recognition, Pattern Recognit. 43 (2) (2010) 4165–4176.

[31] X. He, D. Cai, S. Yan, Neighborhood preserving embedding, in: Proceedings of

ICCV, 2005, pp. 1208–1213.

[32] J. Yang, D. Zhang, J.Y. Yang, et al., Globally maximizing, locally minimizing:

unsupervised discriminant projection with application to face and palm bio-

metrics, IEEE Trans. Pattern Anal. Mach. Intell. 29 (4) (2007) 650–664.

[33] D. Xu, S. Yan, D. Tao, S. Lin, H.J. Zhang, Marginal fisher analysis and its variants

for human gait recognition and content-based image retrieval, IEEE Trans.

Image Process. 16 (11) (2007) 2811–2821.

[34] Hwann-Tzong Chen, Huang-Wei Chang, Tyng-Luh Liu, Local discriminant

embedding and its variants, in: Proceeding of CVPR, 2005, pp. 846–853.

[35] Deng Cai, Xiaofei He, Jiawei Han, Hong-Jiang Zhang, Orthogonal Laplacianfaces

for face recognition, IEEE Trans. Image Process. 15 (11) (2006) 3608–3614.

[36] Jie Gui, Wei Jia, Ling Zhu, Shu-Ling Wang, De-Shuang Huang, Locality pre-

serving discriminant projections for face and palmprint recognition, Neuro-

computing 73 (13–15) (2010) 2696–2707.

[37] J. Lu, Y.P. Tan, G. Wang, Discriminative multimanifold analysis for face recog-

nition from a single training sample per person, IEEE Trans. Pattern Anal.

Mach. Intell. 35 (1) (2013) 39–51.

[38] Y. Pang, Y. Yuan, X. Li, Iterative subspace analysis based on feature line dis-

tance, IEEE Trans. Image Process. 18 (4) (2009) 903–907.

[39] Shuicheng Yan, Dong Xu, Benyu Zhang, Hong-Jiang Zhang, Qiang Yang,

Stephen Lin, Graph embedding and extensions: a general framework for

dimensionality reduction, IEEE Trans. Pattern Anal. Mach. Intell. 29 (1) (2007)

40–51.

[40] Y. Pang, Z. Ji, P. Jing, X. Li, Ranking graph embedding for learning to rerank,

IEEE Trans. Neural Netw. Learn. Syst. 24 (8) (2013) 1292–1303.

[41] Bogdan Raducanua, Fadi Dornaikab, Embedding new observations via sparse-

coding for non-linear manifold learning, Pattern Recognit. 47 (1) (2014)

480–492.

[42] Weizhong Zhang, Lijun Zhang, Yao Hu, Rong Jin, Deng Cai, Xiaofei He, Sparse

learning for stochastic composite optimization, in: Proceedings of AAAI, 2014,

pp. 893–900.

[43] S. Wu, Spectral clustering of high-dimensional data exploiting sparse repre-

sentation vectors, Neurocomputing 135 (2014) 229–239.

[44] Bin Xu, Jianchao Yang, Shuicheng Yan, et al., Learning with L1-graph for image

analysis, IEEE Trans. Image Process. 19 (4) (2010) 858–866.

[45] S. Yan, H. Wang, Semi-supervised learning by sparse representation, in: Pro-

ceedings of SIAM international Conference on Data Mining, 2009, pp. 792–

801.

[46] M. Zheng, J.J. Bu, C. Chen, C. Wang, L.J. Zhang, G. Qiu, D. Cai, Graph regularized

sparse coding for image representation, IEEE Trans. Image Process. 20 (5)

(2011) 1327–1336.

[47] L. Qiao, S. Chen, X. Tan, Sparsity preserving projections with applications to

face recognition, Pattern Recognit. 43 (1) (2010) 331–341.

[48] L.M. Zhang, S. Chen, L. Qiao, Graph optimization for dimensionality reduction

with sparsity constraints, Pattern Recognit. 45 (3) (2012) 1205–1210.

[49] J. Yang, D. Chu, L. Zhang, Y. Xu, J. Yang, Sparse representation classifier steered

discriminative projection with applications to face recognition, IEEE Trans.

Neural Netw. Learn. Syst. 24 (7) (2013) 1023–1035.

[50] Y. Chen, Z. Jin, Reconstructive discriminant analysis: a feature extraction

method induced from linear regression classification, Neurocomputing 87 (15)

(2012) 41–50.

[51] J. Gui, Z. Sun, W. Jia, R. Hu, Y. Lei, S. Ji, Discriminant sparse neighborhood

preserving embedding for face recognition, Pattern Recognit. 45 (8) (2012)

2884–2893.

[52] H. Li, J. Tao, K. Zhang, Efficient and robust feature extraction by maximum

margin criterion, IEEE Trans. Neural Netw. 17 (1) (2006) 157–165.

[53] F. Zang, J. Zhang, Discriminative learning by sparse representation for classi-

fication, Neurocomputing 74 (2011) 2176–2183.

[54] L. Wei, F. Xu, A. Wu, Weighted discriminative sparsity preserving embedding

for face recognition, Knowl.–Based Syst. 57 (2) (2014) 136–145.

[55] E.J. Candes, M.B. Wakin, An introduction to compressive sampling, IEEE Signal

Process. Mag. 25 (2) (2008) 21–30.

[56] D.L. Donoho, Compressed sensing, IEEE Trans. Inf. Theory 52 (4) (2006)

1289–1306.

[57] F.S. Samaria, A.C. Harter, Parameterisation of a stochastic model for human

face identification, in: Proceedings of the Second IEEE Workshop on Appli-

cations of Computer Vision, Sarasota, FL, 1994, pp. 138–142.

[58] A.S. Georghiades, P.N. Belhumeur, D.J. Kriegman, From few to many: illumi-

nation cone models for face recognition under variable lighting and pose, IEEE

Trans. Pattern Anal. Mach. Intell. 23 (2001) 643–660.

[59] A. Martinez, R. Benavente, The AR Face Database, Purdue University, Computer

Vision Center, West Lafayette, 1998, CVC technical report 24 [R].

 

 最后附上原文链接：https://pan.baidu.com/s/1zFIJmuMBp-iIx3KEKLoAug