【ML小结8】降维与度量学习(KNN、PCA、因子分析、LDA)
- 度量学习指距离度量学习,是通过特征变换得到特征子空间,通过使用度量学习,让相似的目标距离更近,不同的目标距离更远.
- 也就是说,度量学习需要得到目标的某些核心特征(特点)。比如区分两个人,2只眼睛1个鼻子-这是共性,柳叶弯眉樱桃口-这是特点。
- 度量学习分为两种,一种是基于监督学习,另外一种是基于非监督学习(主要指降维方法,即对于高维数据,在尽可能保留原始变量信息的基础上,降低变量维度)。
1. KNN
有监督学习
生成式模型
1.1 工作机制
给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个“邻居”的信息进行预测。
(分类中用投票法,回归中用平均法,还可以基于距离远近进行加权投票或平均。)
注意:KNN没有显示的训练过程,它是“懒惰学习”的代表,它在训练阶段只是把数据保存下来,训练时间开销为0,等收到测试样本后进行处理。
1.2 错误率上下界
KNN错误率的上下界在1-2倍贝叶斯决策方法的错误率范围内。
以最近邻分类器(K=1)在二分类问题为例:
令 c ∗ = a r g m a x c ∈ Y P ( c ∣ x ) c^*=argmax_{c \in \mathcal Y}P(c|x) c∗=argmaxc∈YP(c∣x)表示贝叶斯最优分类器的结果。P(c|x)表示预测x属于类标c的概率。给定测试样本x,若其最近邻样本为z,则1NN出错的概率为:
P ( e r r ) P(err) P(err) 出错的概率为x与z类标不同的概率
= 1 − ∑ c ∈ Y P ( c ∣ x ) P ( c ∣ z ) =1-\sum_{c \in \mathcal Y}P(c|x)P(c|z) =1−∑c∈YP(c∣x)P(c∣z) # 也就是1-x与z类标相同的概率
≈ 1 − ∑ c ∈ Y P 2 ( c ∣ x ) \approx 1-\sum_{c \in \mathcal Y}P^2(c|x) ≈1−∑c∈YP2(c∣x)
≤ 1 − P 2 ( c ∗ ∣ x ) \le1-P^2(c^*|x) ≤1−P2(c∗∣x) # 1减去那么多项自然小于1减去其中1项
= ( 1 + P ( c ∗ ∣ x ) ) ( 1 − P ( c ∗ ∣ x ) ) =(1+P(c^*|x))(1-P(c^*|x)) =(1+P(c∗∣x))(1−P(c∗∣x))
由 P ( c ∗ ∣ x ) < 1 , 1 + P ( c ∗ ∣ x ) > 1 P(c^*|x)<1,1+P(c^*|x)>1 P(c∗∣x)<1,1+P(c∗∣x)>1有
1 − P ( c ∗ ∣ x ) ≤ ( 1 + P ( c ∗ ∣ x ) ) ( 1 − P ( c ∗ ∣ x ) ) ≤ 2 ( 1 − P ( c ∗ ∣ x ) ) 1-P(c^*|x)\le(1+P(c^*|x))(1-P(c^*|x))\le2(1-P(c^*|x)) 1−P(c∗∣x)≤(1+P(c∗∣x))(1−P(c∗∣x))≤2(1−P(c∗∣x))
1.3 实现:kd树
knn的实现需要考虑如何快速搜索k个最近邻点。kd树是一种便于在k维空间中的数据进行快速检索的数据结构。利用kd树可以节省对大部分数据点的搜索,从而减少搜索的计算量。
Kd-树是K-dimension tree的缩写,是对数据点在k维空间中划分的一种数据结构,主要应用在高维数据索引(如:范围搜索和最近邻搜索)。本质上说,Kd-树就是一种平衡二叉树。
平衡二叉树:二叉树中每个节点的左、右子树的高度至多相差1
注意:这里的k与knn的k不同。
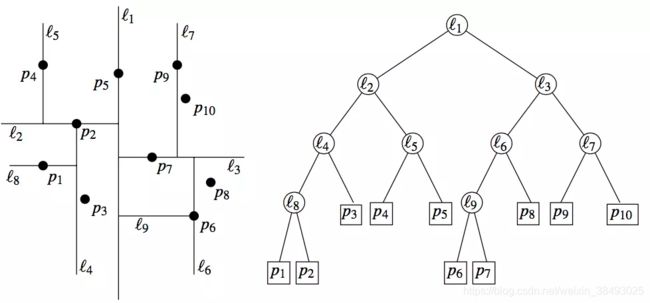
参考:基础-12:15分钟理解KD树 - 简书
https://www.jianshu.com/p/ffe52db3e12b
2. 主成分分析(PCA)
无监督学习
主成分分析通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
2.0 数据预处理
均值为0,特征方差归一
2.1 模型表示
设投影矩阵为W,样本点 x i x_i xi在新空间超平面上的投影是 W T x i W^Tx_i WTxi。我们希望所有样本点的投影能够尽可能地分开,所以目标是使得投影后样本点的方差最大化。
由于这些样本点的每一维特征均值都为0,因此投影后的均值仍然是0。故方差为:
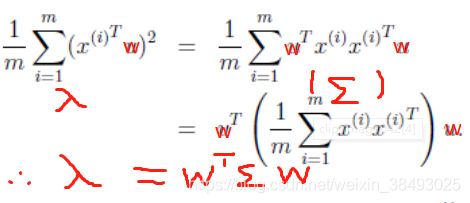
括号中的一项即为协方差矩阵Σ(详见引用处关于自协方差矩阵的介绍,这里是均值为0的情况)!由此可见,协方差矩阵Σ与投影的方向w无关,只与数据集中的样本有关,因此协方差矩阵完全决定了数据的分布及变化情况。
最后,模型表示如下:
max W t r ( W T X X T W ) \max_W\quad tr(W^TXX^TW) Wmaxtr(WTXXTW) s . t . W T W = I s.t.\quad W^TW=I s.t.WTW=I
矩阵的迹 就是 矩阵的主对角线上所有元素的和。
协方差矩阵:协方差是对两个随机变量联合分布线性相关程度的一种度量。两个随机变量越线性相关,协方差越大;完全线性无关,协方差为零。 c o v ( X , Y ) = E [ ( X − E [ X ] ) ( Y − E [ Y ] ) ] cov(X,Y)=E[(X−E[X])(Y−E[Y])] cov(X,Y)=E[(X−E[X])(Y−E[Y])]
自协方差矩阵:
参考:主成分分析(Principal components analysis)-最大方差解释 - JerryLead - 博客园
http://www.cnblogs.com/jerrylead/archive/2011/04/18/2020209.html
2.2 模型求解
等式条件下求解最优问题用拉格朗日乘子法,得:
X X T w i = λ i w i XX^Tw_i=\lambda_iw_i XXTwi=λiwi
于是,只需要对协方差矩阵 X X T XX^T XXT进行特征值分解,将特征值降序排序,前d个特征值所对应的特征向量即为投影矩阵W。
2.3 缺点
- 主成分提取后命名不容易
- 主成分与每个原始变量的相关程度大小没能反映出来
3. 因子分析
针对主成分分析的缺点,提出了因子分析。因子分析是在主成分分析的基础上,通过因子旋转,体现每个主成分与原始变量的相关程度,从而辅助公共因子命名,以便对实际问题进行分析。
3.1 假设条件
1)原始变量 X i X_i Xi是正态随机变量,且已标准化, 即 E ( X i ) = 0 , D ( X i ) = 1 E(X_i)=0,D(X_i)=1 E(Xi)=0,D(Xi)=1
2) 公共因子 F i F_i Fi相互独立,且已标准化,即 E ( F i ) = 0 , D ( F i ) = 1 E(F_i)=0,D(F_i)=1 E(Fi)=0,D(Fi)=1
3) 特殊因子 ε i \varepsilon_i εi相互独立,且 E ( ε i ) = 0 , D ( ε i ) = σ 2 E(\varepsilon_i)=0,D(\varepsilon_i)= \sigma^2 E(εi)=0,D(εi)=σ2
4) 公共因子 F i F_i Fi与特殊因子 ε j \varepsilon_j εj相互独立.
3.2 模型表示


对于多维原始变量中的每一变量,都采用公共因子与特殊因子的线性组合表示。

3.3 变量意义
- 因子载荷: R ( X i , F j ) = c o v ( X i , F j ) D X i D F j = . . . = a i j R(X_i,F_j)=\frac{cov(X_i,F_j)}{\sqrt {DX_i}\sqrt {DF_j}}=...=a_{ij} R(Xi,Fj)=DXiDFjcov(Xi,Fj)=...=aij表示原始变量与公因子的相关程度。反映了第i 个变量在第j个公共因子上的相对重要性。为因子命名做准备。
- 变量 X i X_i Xi的共同度: h i 2 = ∑ j = 1 m a i j 2 h_i^2=\sum_{j=1}^m a_{ij}^2 hi2=j=1∑maij2代表 X i X_i Xi方差( D ( X i ) = h i 2 + σ i 2 D(X_i)=h_i^2+\sigma_i^2 D(Xi)=hi2+σi2)的主要部分,共同度越大说明公共因子包含 X i X_i Xi的变异信息越多。
- 公共因子 F j F_j Fj对X的方差贡献: ∑ i = 1 p a i j 2 \sum_{i=1}^p a_{ij}^2 i=1∑paij2方差贡献越大,则该公共因子越重要。
3.4 因子旋转
- 目的:辅助因子命名
- 方法:采用方差最大正交旋转,用一个正交阵右乘因子载荷矩阵。
- 结果:因子旋转后的因子载荷矩阵每个变量仅在一个公共因子上有较大的载荷,在其余公共因子上载荷较小
3.5 计算步骤
反求、因子载荷矩阵、因子旋转
step1:将原始数据标准化。
step2:建立变量的协方差矩阵 X X T XX^T XXT。
step3:求协方差矩阵的特征根及其相应的单位特征向量。
step4:对因子载荷矩阵施行方差最大正交旋转。
step5:计算因子得分。
4. 线性判别分析(LDA)
有监督学习
与PCA保持数据信息不同,LDA是为了使得降维后的数据点尽可能地容易被区分!
4.1 算法思想
LDA的思想非常朴素:将带上标签的数据(点),通过投影(变换)的方法,投影到更低维的空间。在这个低维空间中,同类样本尽可能接近,异类样本尽可能远离。一句话概括,就是“投影后类内方差最小,类间方差最大”。
4.2 模型表示
令 μ i \mu_i μi和 ∑ i \sum_i ∑i分别表示第 i i i类原始样本的均值向量和协方差矩阵。 μ i = ∑ x ∈ X i x i N i \mu_i=\frac{\sum_{x\in X_i} x_i}{N_i} μi=Ni∑x∈Xixi ∑ i = ∑ x ∈ X i ( x − μ i ) ( x − μ i ) T \sum_{i}=\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T i∑=x∈Xi∑(x−μi)(x−μi)T
以二类LDA为例,则 i ∈ { 0 , 1 } i\in\{0,1\} i∈{0,1}。
由于是两类数据,因此我们只需要将数据投影到一条直线上即可。假设我们的投影直线是向量 w w w,则对任意一个样本 x i x_i xi,它在直线 w w w的投影为 w T x i w^Tx_i wTxi,对于两个类别的中心点 μ 0 , μ 1 μ0,μ1 μ0,μ1,在直线 w w w的投影为 w T μ 0 w^Tμ_0 wTμ0和 w T μ 1 w^Tμ_1 wTμ1
4.2.1 类内方差
欲使同类样本的投影点尽可能接近,可以让同类样本的投影点的协方差尽可能小。
类内散度矩阵: S w = ∑ 0 + ∑ 1 = ∑ x ∈ X 0 ( x − μ 0 ) ( x − μ 0 ) T + ∑ x ∈ X 1 ( x − μ 1 ) ( x − μ 1 ) T S_w=\sum_0+\sum_1=\sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^T+\sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^T Sw=0∑+1∑=x∈X0∑(x−μ0)(x−μ0)T+x∈X1∑(x−μ1)(x−μ1)T最小化类内方差: a r g m i n w T S w w argmin\quad w^TS_ww argminwTSww
4.2.2 类间方差
欲使异类样本的投影点尽可能远离,可以让异类样本的类中心之间的距离尽可能大。
类间散度矩阵: S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T Sb=(μ0−μ1)(μ0−μ1)T最大化类间方差: a r g m a x w T S b w argmax \quad w^TS_bw argmaxwTSbw
4.2.3 优化目标
使得投影后类内方差最小,类间方差最大 a r g m a x J ( w ) = w T S b w w T S w w argmax\quad J(w)=\frac{w^TS_bw}{w^TS_ww} argmaxJ(w)=wTSwwwTSbw由于分子分母都是矩阵,要将矩阵变成实数,可以取矩阵的行列式或者矩阵的迹。其中,矩阵的行列式等于矩阵特征值之积,矩阵的迹等于矩阵特征值之和。所以优化目标可以转化为: a r g m a x J ( w ) = t r ( w T S b w ) t r ( w T S w w ) argmax\quad J(w)=\frac{tr(w^TS_bw)}{tr(w^TS_ww)} argmaxJ(w)=tr(wTSww)tr(wTSbw)
4.3 模型求解
通过如下广义特征值求解: S b W = λ S w W S_bW=λS_wW SbW=λSwWW的解则是 S w − 1 S b S^{−1}_wS_b Sw−1Sb的N-1个最大广义特征值所对应的特征向量按列组成的矩阵。
4.4 推广:多类LDA
4.5 优缺点
LDA算法既可以用来降维,又可以用来分类,但是目前来说,主要还是用于降维。
4.5.1 主要优点
1)在降维过程中可以使用类别的先验知识经验,而像PCA这样的无监督学习则无法使用类别先验知识。
2)LDA在样本分类信息依赖均值而不是方差的时候,比PCA之类的算法较优。
4.5.2 主要缺点
1)LDA不适合对非高斯分布样本进行降维,PCA也有这个问题。
2)LDA降维最多降到类别数k-1的维数,如果我们降维的维度大于k-1,则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
3)LDA在样本分类信息依赖方差而不是均值的时候,降维效果不好。
4)LDA可能过度拟合数据。
4.6 参考教程
- 线性判别分析LDA原理总结 - 刘建平Pinard - 博客园
http://www.cnblogs.com/pinard/p/6244265.html - 数据降维之LDA&PCA - zxhohai的博客 - CSDN博客
https://blog.csdn.net/hohaizx/article/details/78165786



