最小生成树以及Kruskal算法，Prime算法

一、最小生成树

连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任 意一对顶点都是连通的，则称此图为连通图。
强连通图：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj 到 vi的路径，则称此图是强连通图。
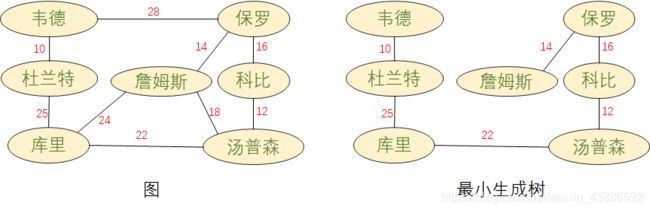
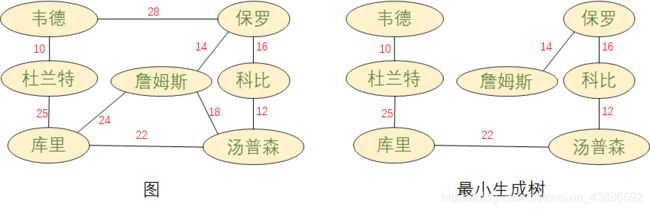
生成树：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点 和n- 1条边连通图中的每一棵生成树，都是原图的一个极大无环子图，即从其中删去任何一条边，生成树就不在连通；反之，在其中引入任何一条新边，都会形成一条回路。生成树可能有多个。
最小生成树:所有生成树边的权值加起来最小的就是最小
若连通图由n个顶点组成，则生成树。
其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三条：

• 只能使用图中的边来构造最小生成树
• 只能使用恰好n-1条边来连接图中的n个顶点
• 选用的n-1条边不能构成回路

构造最小生成树的方法：Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。

二、 Kruskal算法

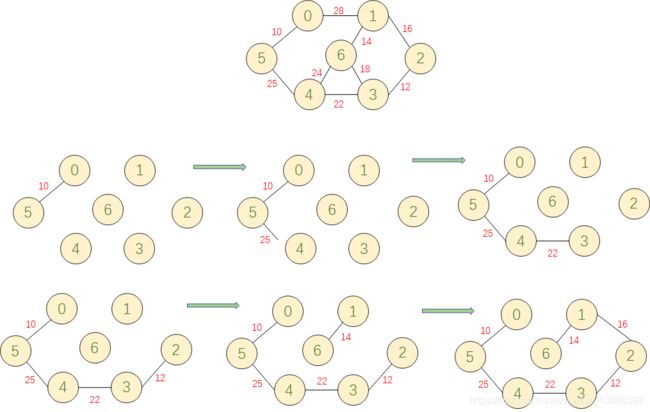
任给一个有n个顶点的连通网络N={V,E}， 首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL}，其中每个顶点自成一个连通分量， 其次不断从E中取出权值最小的一条边(若有多条任取其一)，若该边的两个顶点来自不同的连通分 量，则将此边加入到G中。
如此重复，直到所有顶点在同一个连通分量上为止。 核心：每次迭代时，选出一条具有最小权值，且两端点不在同一连通分量上的边，加入生成树

注意：

1.在每次选择最小权值的时候，要判断选择最小权值的节点是否会和原来的节点形成环，此时就需要使用到并查集，将已加入的节点同时加入并查集，每次找到新节点添加时，首先判断是否会添加在一个子集中，如果是一个集合，就不要这个边。
2.克鲁斯卡尔算法是一个贪心算法，生成的最小生成树所有去权并不绝对

#include
#include
#include
#include
#include
using namespace std;

namespace Kruskal//Kruskal算法
{
	//顶点的值类型V和边的类型W,D为true是代表有向图，false代表无向图
	template<class V, class W, bool D = false>
	class Graph
	{
	private:
		vector<V> m_vertex;//顶点集合
		vector<int> m_arr;//并查集集合，检测环
		map<W, pair<int, int>> m_map;//边集合
		unordered_map<V, int> m_pos;//方便直接找到顶点下标
	public:
		Graph(const V* a, int n)//构造函数
		{
			m_vertex.resize(n);
			m_arr.resize(n, -1);
			for (int i = 0; i < n; i++)
			{
				m_vertex[i] = a[i];
				m_pos[a[i]] = i;
			}
		}

		int Find(int index)//查找元素在哪个集合中
		{
			while (m_arr[index] >= 0)
			{
				index = m_arr[index];
			}
			return index;
		}

		bool Union(int srcindex, int detindex)
		{
			if (srcindex == detindex)//相同顶点不能合并
			{
				return false;
			}
			m_arr[srcindex] += m_arr[detindex];//det合并到src中
			m_arr[detindex] = srcindex;
			return true;

		}

		//获取顶点src在矩阵中的下标
		int GetPosInMatrix(const V& src)
		{
			if (m_pos.find(src) != m_pos.end())
			{
				return m_pos[src];
			}
			throw invalid_argument("非法顶点");
		}

		//添加一条从src到det权重为weight的边
		void AddEdge(const V& src, const V& det, const W& weight)
		{
			int srcIndex = GetPosInMatrix(src);
			int detIndex = GetPosInMatrix(det);
			m_map[weight] = { srcIndex, detIndex };//合并两条边

		}

		void kruskal()
		{
			W Sum = W();
			auto mit = m_map.begin();
			for (int i = 0; i < m_vertex.size() - 1; i++, mit++)//n个顶点，最小生成树有n-1个边
			{
				int x = Find(mit->second.first);
				int y = Find(mit->second.second);
				if (Union(x, y) == false)//两个顶点属于一个集合，不能合并会形成环
				{
					i--;//不能合并时，i++会少算一条边，这里需要和循环里面的++抵消
					continue;
				}
				Sum += mit->first;
				cout << m_vertex[mit->second.first] << "[" << mit->second.first << "] ---(" << mit->first << ")---";
				cout << m_vertex[mit->second.second] << "[" << mit->second.second << "]\n";
			}
			cout << "最小生成树的总权值：" << Sum << endl;
		}
	};

	void TestGraph()
	{
			string a[7] = { "韦德", "杜兰特", "库里", "詹姆斯", "保罗", "科比", "汤普森" };
			Graph<string, int> g(a, 7);
			g.AddEdge("詹姆斯", "汤普森", 18);
			g.AddEdge("詹姆斯", "库里", 24);
			g.AddEdge("詹姆斯", "保罗", 14);
			g.AddEdge("库里", "汤普森", 22);
			g.AddEdge("库里", "杜兰特", 25);
			g.AddEdge("韦德", "杜兰特", 10);
			g.AddEdge("韦德", "保罗", 28);
			g.AddEdge("科比", "保罗", 16);
			g.AddEdge("科比", "汤普森", 12);
			cout << "Kruskal :\n";
			g.kruskal();
	}
}

二、Prime算法

首先选出权值最小的边，接着从已经选出的边中选出
连接边最小的，直至选出n-1个边，这样把图分成两部分:连同的和不连通的，就完美的避开了环的问题。

namespace Prime//Prime算法
{
	//顶点的值类型V和边的类型W,D为true是代表有向图，false代表无向图
	template<class V, class W, bool D = false>
	class Graph
	{
	private:
		pair<W, pair<int, int>> m_min;//存储最小的边
		vector<V> m_vertex;//顶点集合
		vector<vector<W>> m_line;//边集合
		unordered_map<V, int> m_pos;//顶点的值对应在顶点集合中的下标,
	public:
		Graph(const V* a, int n)//构造函数
		{
			m_vertex.resize(n);
			m_line.resize(n);
			m_min = { INT_MAX, { -1 , -1 } };
			for (int i = 0; i < n; i++)
			{
				m_vertex[i] = a[i];
				m_line[i].resize(n, W());
				m_pos[a[i]] = i;
			}
		}

		//获取顶点src在矩阵中的下标
		int GetPosInMatrix(const V& src)
		{
			if (m_pos.find(src) != m_pos.end())
			{
				return m_pos[src];
			}
			throw invalid_argument("非法顶点");
		}
		//添加一条从src到det权重为weight的边
		void AddEdge(const V& src, const V& det, const W& weight)
		{
			//1.先获取两个顶点在矩阵中的下标
			int srcIndex = GetPosInMatrix(src);
			int detIndex = GetPosInMatrix(det);
			if (m_line[srcIndex][detIndex] != W())//这条边已经存在了,不用在插入
			{
				return;
			}

			if (m_min.first > weight)//找到最小的边
			{
				m_min.first = weight;
				m_min.second = { srcIndex, detIndex };
			}

			//2.修改邻接矩阵中的值
			m_line[srcIndex][detIndex] = weight;
			if (D == false)//无向图要添加两条边
			{
				m_line[detIndex][srcIndex] = weight;
			}
		}

		void prime()
		{
			W Sum = W();
			//1.初始化，找到最小的边，就是m_pos的begin()位置
			unordered_set<int> s;//存储已经找到的顶点的下标
			s.insert(m_min.second.first);
			s.insert(m_min.second.second);
			Sum += m_min.first;
			cout << m_vertex[m_min.second.first] << "[" << m_min.second.first << "] ---(" << m_min.first << ")---";
			cout << m_vertex[m_min.second.second] << "[" << m_min.second.second << "]\n";
			//2.寻找找到节点中相连边的最小值
			
			for (int i = 1; i < m_vertex.size()-1; i++)
			{
				pair<W, pair<int, int>> min = { INT_MAX, { -1, -1 } };
				for (auto& e : s)
				{
					for (int i = 0; i < m_vertex.size(); i++)
					{
						if (m_line[e][i] != W() && s.find(i) == s.end())//边存在且连接的节点不在s中
						{
							min.first = min.first > m_line[e][i] ? m_line[e][i] : min.first;
							min.second = { e, i };
						}
					}
					
				}
				cout << m_vertex[min.second.first] << "[" << min.second.first << "] ---(" << min.first << ")---";
				cout << m_vertex[min.second.second] << "[" << min.second.second << "]\n";
				s.insert(min.second.second);
				Sum += min.first;
			}
			cout << "最小生成树的总权值：" << Sum << endl;
		}
	};

	void TestGraph()
	{
		string a[7] = { "韦德", "杜兰特", "库里", "詹姆斯", "保罗", "科比", "汤普森" };
		Prime::Graph<string, int> g(a, 7);
		g.AddEdge("詹姆斯", "汤普森", 18);
		g.AddEdge("詹姆斯", "库里", 24);
		g.AddEdge("詹姆斯", "保罗", 14);
		g.AddEdge("库里", "汤普森", 22);
		g.AddEdge("库里", "杜兰特", 25);
		g.AddEdge("韦德", "杜兰特", 10);
		g.AddEdge("韦德", "保罗", 28);
		g.AddEdge("科比", "保罗", 16);
		g.AddEdge("科比", "汤普森", 12);
		cout << "Prime :\n";
		g.prime();
	}
}