LDA和PCA降维总结
文章目录
- 线性判别分析(LDA)
- LDA思想总结
- 图解LDA核心思想
- 二类LDA算法原理
- LDA算法流程总结
- LDA和PCA区别
- LDA优缺点
- 主成分分析(PCA)
- 主成分分析(PCA)思想总结
- 图解PCA核心思想
- PCA算法推理
- PCA算法流程总结
- PCA算法主要优缺点
- 降维的必要性及目的
- KPCA与PCA的区别
线性判别分析(LDA)
LDA思想总结
线性判别分析(Linear Discriminant Analysis,LDA)是一种经典的降维方法。和主成分分析PCA不考虑样本类别输出的无监督降维技术不同,LDA是一种监督学习的降维技术,数据集的每个样本有类别输出。
LDA分类思想简单总结如下:
- 多维空间中,数据处理分类问题较为复杂,LDA算法将多维空间中的数据投影到一条直线上,将d维数据转化成1维数据进行处理。
- 对于训练数据,设法将多维数据投影到一条直线上,同类数据的投影点尽可能接近,异类数据点尽可能远离。
- 对数据进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定样本的类别。
如果用一句话概括LDA思想,即“投影后类内方差最小,类间方差最大”。
图解LDA核心思想
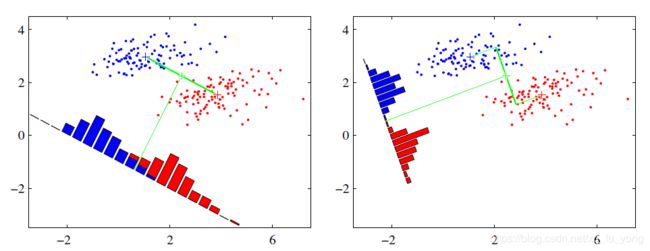
假设有红、蓝两类数据,这些数据特征均为二维,如下图所示。我们的目标是将这些数据投影到一维,让每一类相近的数据的投影点尽可能接近,不同类别数据尽可能远,即图中红色和蓝色数据中心之间的距离尽可能大。
左图和右图是两种不同的投影方式。
左图思路:让不同类别的平均点距离最远的投影方式。
右图思路:让同类别的数据挨得最近的投影方式。
从上图直观看出,右图红色数据和蓝色数据在各自的区域来说相对集中,根据数据分布直方图也可看出,所以右图的投影效果好于左图,左图中间直方图部分有明显交集。
以上例子是基于数据是二维的,分类后的投影是一条直线。如果原始数据是多维的,则投影后的分类面是一低维的超平面。
二类LDA算法原理
输入:数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D=\{(\boldsymbol x_1,\boldsymbol y_1),(\boldsymbol x_2,\boldsymbol y_2),...,(\boldsymbol x_m,\boldsymbol y_m)\} D={(x1,y1),(x2,y2),...,(xm,ym)},其中样本 x i \boldsymbol x_i xi 是n维向量, y i ϵ { 0 , 1 } \boldsymbol y_i \epsilon \{0, 1\} yiϵ{0,1},降维后的目标维度 d d d。定义
N j ( j = 0 , 1 ) N_j(j=0,1) Nj(j=0,1) 为第 j j j 类样本个数;
X j ( j = 0 , 1 ) X_j(j=0,1) Xj(j=0,1) 为第 j j j 类样本的集合;
u j ( j = 0 , 1 ) u_j(j=0,1) uj(j=0,1) 为第 j j j 类样本的均值向量;
∑ j ( j = 0 , 1 ) \sum_j(j=0,1) ∑j(j=0,1) 为第 j j j 类样本的协方差矩阵。
其中
u j = 1 N j ∑ x ϵ X j x ( j = 0 , 1 ) , ∑ j = ∑ x ϵ X j ( x − u j ) ( x − u j ) T ( j = 0 , 1 ) u_j = \frac{1}{N_j} \sum_{\boldsymbol x\epsilon X_j}\boldsymbol x(j=0,1), \sum_j = \sum_{\boldsymbol x\epsilon X_j}(\boldsymbol x-u_j)(\boldsymbol x-u_j)^T(j=0,1) uj=Nj1xϵXj∑x(j=0,1),j∑=xϵXj∑(x−uj)(x−uj)T(j=0,1)
假设投影直线是向量 w \boldsymbol w w,对任意样本 x i \boldsymbol x_i xi,它在直线 w w w上的投影为 w T x i \boldsymbol w^Tx_i wTxi,两个类别的中心点 u 0 u_0 u0, $u_1 $在直线 w w w 的投影分别为 w T u 0 \boldsymbol w^Tu_0 wTu0 、 w T u 1 \boldsymbol w^Tu_1 wTu1。
LDA的目标是让两类别的数据中心间的距离 ∥ w T u 0 − w T u 1 ∥ 2 2 \| \boldsymbol w^Tu_0 - \boldsymbol w^Tu_1 \|^2_2 ∥wTu0−wTu1∥22 尽量大,与此同时,希望同类样本投影点的协方差 w T ∑ 0 w \boldsymbol w^T \sum_0 \boldsymbol w wT∑0w、 w T ∑ 1 w \boldsymbol w^T \sum_1 \boldsymbol w wT∑1w 尽量小,最小化 w T ∑ 0 w − w T ∑ 1 w \boldsymbol w^T \sum_0 \boldsymbol w - \boldsymbol w^T \sum_1 \boldsymbol w wT∑0w−wT∑1w 。
定义
类内散度矩阵
S w = ∑ 0 + ∑ 1 = ∑ x ϵ X 0 ( x − u 0 ) ( x − u 0 ) T + ∑ x ϵ X 1 ( x − u 1 ) ( x − u 1 ) T S_w = \sum_0 + \sum_1 = \sum_{\boldsymbol x\epsilon X_0}(\boldsymbol x-u_0)(\boldsymbol x-u_0)^T + \sum_{\boldsymbol x\epsilon X_1}(\boldsymbol x-u_1)(\boldsymbol x-u_1)^T Sw=0∑+1∑=xϵX0∑(x−u0)(x−u0)T+xϵX1∑(x−u1)(x−u1)T
类间散度矩阵 S b = ( u 0 − u 1 ) ( u 0 − u 1 ) T S_b = (u_0 - u_1)(u_0 - u_1)^T Sb=(u0−u1)(u0−u1)T
据上分析,优化目标为
arg max w J ( w ) = ∥ w T u 0 − w T u 1 ∥ 2 2 w T ∑ 0 w + w T ∑ 1 w = w T ( u 0 − u 1 ) ( u 0 − u 1 ) T w w T ( ∑ 0 + ∑ 1 ) w = w T S b w w T S w w \mathop{\arg\max}_\boldsymbol w J(\boldsymbol w) = \frac{\| \boldsymbol w^Tu_0 - \boldsymbol w^Tu_1 \|^2_2}{\boldsymbol w^T \sum_0\boldsymbol w + \boldsymbol w^T \sum_1\boldsymbol w} = \frac{\boldsymbol w^T(u_0-u_1)(u_0-u_1)^T\boldsymbol w}{\boldsymbol w^T(\sum_0 + \sum_1)\boldsymbol w} = \frac{\boldsymbol w^TS_b\boldsymbol w}{\boldsymbol w^TS_w\boldsymbol w} argmaxwJ(w)=wT∑0w+wT∑1w∥wTu0−wTu1∥22=wT(∑0+∑1)wwT(u0−u1)(u0−u1)Tw=wTSwwwTSbw
根据广义瑞利商的性质,矩阵 S w − 1 S b S^{-1}_{w} S_b Sw−1Sb 的最大特征值为 J ( w ) J(\boldsymbol w) J(w) 的最大值,矩阵 S w − 1 S b S^{-1}_{w} S_b Sw−1Sb 的最大特征值对应的特征向量即为 w \boldsymbol w w。
LDA算法流程总结
LDA算法降维流程如下:
输入:数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D = \{ (x_1,y_1),(x_2,y_2), ... ,(x_m,y_m) \} D={(x1,y1),(x2,y2),...,(xm,ym)},其中样本 x i x_i xi 是n维向量, y i ϵ { C 1 , C 2 , . . . , C k } y_i \epsilon \{C_1, C_2, ..., C_k\} yiϵ{C1,C2,...,Ck},降维后的目标维度 d d d 。
输出:降维后的数据集 D ‾ \overline{D} D 。
步骤:
- 计算类内散度矩阵 S w S_w Sw。
- 计算类间散度矩阵 S b S_b Sb 。
- 计算矩阵 S w − 1 S b S^{-1}_wS_b Sw−1Sb 。
- 计算矩阵 S w − 1 S b S^{-1}_wS_b Sw−1Sb 的最大的 d 个特征值。
- 计算 d 个特征值对应的 d 个特征向量,记投影矩阵为 W 。
- 转化样本集的每个样本,得到新样本 P i = W T x i P_i = W^Tx_i Pi=WTxi 。
- 输出新样本集 D ‾ = { ( p 1 , y 1 ) , ( p 2 , y 2 ) , . . . , ( p m , y m ) } \overline{D} = \{ (p_1,y_1),(p_2,y_2),...,(p_m,y_m) \} D={(p1,y1),(p2,y2),...,(pm,ym)}
LDA和PCA区别
| 异同点 | LDA | PCA |
|---|---|---|
| 相同点 | 1. 两者均可以对数据进行降维; 2. 两者在降维时均使用了矩阵特征分解的思想; 3. 两者都假设数据符合高斯分布; |
|
| 不同点 | 有监督的降维方法; | 无监督的降维方法; |
| 降维最多降到k-1维; | 降维多少没有限制; | |
| 可以用于降维,还可以用于分类; | 只用于降维; | |
| 选择分类性能最好的投影方向; | 选择样本点投影具有最大方差的方向; | |
| 更明确,更能反映样本间差异; | 目的较为模糊; |
LDA优缺点
| 优缺点 | 简要说明 |
|---|---|
| 优点 | 1. 可以使用类别的先验知识; 2. 以标签、类别衡量差异性的有监督降维方式,相对于PCA的模糊性,其目的更明确,更能反映样本间的差异; |
| 缺点 | 1. LDA不适合对非高斯分布样本进行降维; 2. LDA降维最多降到分类数k-1维; 3. LDA在样本分类信息依赖方差而不是均值时,降维效果不好; 4. LDA可能过度拟合数据。 |
主成分分析(PCA)
主成分分析(PCA)思想总结
- PCA就是将高维的数据通过线性变换投影到低维空间上去。
- 投影思想:找出最能够代表原始数据的投影方法。被PCA降掉的那些维度只能是那些噪声或是冗余的数据。
- 去冗余:去除可以被其他向量代表的线性相关向量,这部分信息量是多余的。
- 去噪声,去除较小特征值对应的特征向量,特征值的大小反映了变换后在特征向量方向上变换的幅度,幅度越大,说明这个方向上的元素差异也越大,要保留。
- 对角化矩阵,寻找极大线性无关组,保留较大的特征值,去除较小特征值,组成一个投影矩阵,对原始样本矩阵进行投影,得到降维后的新样本矩阵。
- 完成PCA的关键是——协方差矩阵。协方差矩阵,能同时表现不同维度间的相关性以及各个维度上的方差。协方差矩阵度量的是维度与维度之间的关系,而非样本与样本之间。
- 之所以对角化,因为对角化之后非对角上的元素都是0,达到去噪声的目的。对角化后的协方差矩阵,对角线上较小的新方差对应的就是那些该去掉的维度。所以我们只取那些含有较大能量(特征值)的维度,其余的就舍掉,即去冗余。
图解PCA核心思想
PCA可解决训练数据中存在数据特征过多或特征累赘的问题。核心思想是将m维特征映射到n维(n < m),这n维形成主元,是重构出来最能代表原始数据的正交特征。
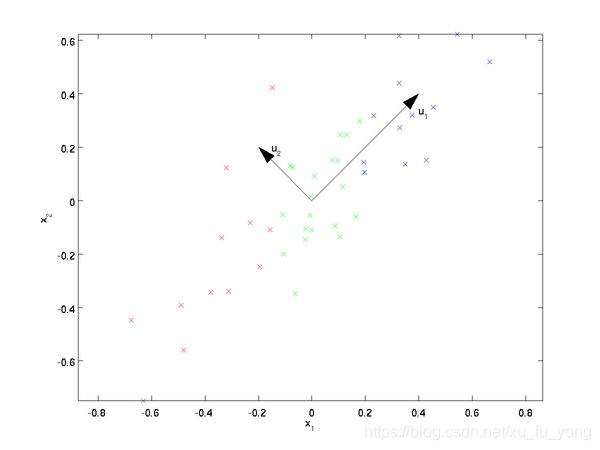
假设数据集是m个n维, ( x ( 1 ) , x ( 2 ) , ⋯ , x ( m ) ) (\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, \cdots, \boldsymbol x^{(m)}) (x(1),x(2),⋯,x(m))。如果 n = 2 n=2 n=2,需要降维到 n ′ = 1 n'=1 n′=1,现在想找到某一维度方向代表这两个维度的数据。下图有 u 1 , u 2 u_1, u_2 u1,u2两个向量方向,但是哪个向量才是我们所想要的,可以更好代表原始数据集的呢?
从图可看出, u 1 u_1 u1比 u 2 u_2 u2好,为什么呢?有以下两个主要评价指标:
- 样本点到这个直线的距离足够近。
- 样本点在这个直线上的投影能尽可能的分开。
如果我们需要降维的目标维数是其他任意维,则:
- 样本点到这个超平面的距离足够近。
- 样本点在这个超平面上的投影能尽可能的分开。
PCA算法推理
下面以基于最小投影距离为评价指标推理:
假设数据集是m个n维, ( x ( 1 ) , x ( 2 ) , . . . , x ( m ) ) (x^{(1)}, x^{(2)},...,x^{(m)}) (x(1),x(2),...,x(m)),且数据进行了中心化。经过投影变换得到新坐标为 w 1 , w 2 , . . . , w n {w_1,w_2,...,w_n} w1,w2,...,wn,其中 w w w 是标准正交基,即 ∥ w ∥ 2 = 1 \| w \|_2 = 1 ∥w∥2=1, w i T w j = 0 w^T_iw_j = 0 wiTwj=0。
经过降维后,新坐标为 { w 1 , w 2 , . . . , w n } \{ w_1,w_2,...,w_n \} {w1,w2,...,wn},其中 n ′ n' n′ 是降维后的目标维数。样本点 x ( i ) x^{(i)} x(i) 在新坐标系下的投影为 z ( i ) = ( z 1 ( i ) , z 2 ( i ) , . . . , z n ′ ( i ) ) z^{(i)} = \left(z^{(i)}_1, z^{(i)}_2, ..., z^{(i)}_{n'} \right) z(i)=(z1(i),z2(i),...,zn′(i)),其中 z j ( i ) = w j T x ( i ) z^{(i)}_j = w^T_j x^{(i)} zj(i)=wjTx(i) 是 x ( i ) x^{(i)} x(i) 在低维坐标系里第 j 维的坐标。
如果用 z ( i ) z^{(i)} z(i) 去恢复 x ( i ) x^{(i)} x(i) ,则得到的恢复数据为 x ^ ( i ) = ∑ j = 1 n ′ x j ( i ) w j = W z ( i ) \widehat{x}^{(i)} = \sum^{n'}_{j=1} x^{(i)}_j w_j = Wz^{(i)} x (i)=∑j=1n′xj(i)wj=Wz(i),其中 W W W为标准正交基组成的矩阵。
考虑到整个样本集,样本点到这个超平面的距离足够近,目标变为最小化 ∑ i = 1 m ∥ x ^ ( i ) − x ( i ) ∥ 2 2 \sum^m_{i=1} \| \hat{x}^{(i)} - x^{(i)} \|^2_2 ∑i=1m∥x^(i)−x(i)∥22 。对此式进行推理,可得:
∑ i = 1 m ∥ x ^ ( i ) − x ( i ) ∥ 2 2 = ∑ i = 1 m ∥ W z ( i ) − x ( i ) ∥ 2 2 = ∑ i = 1 m ( W z ( i ) ) T ( W z ( i ) ) − 2 ∑ i = 1 m ( W z ( i ) ) T x ( i ) + ∑ i = 1 m ( x ( i ) ) T x ( i ) = ∑ i = 1 m ( z ( i ) ) T ( z ( i ) ) − 2 ∑ i = 1 m ( z ( i ) ) T x ( i ) + ∑ i = 1 m ( x ( i ) ) T x ( i ) = − ∑ i = 1 m ( z ( i ) ) T ( z ( i ) ) + ∑ i = 1 m ( x ( i ) ) T x ( i ) = − t r ( W T ( ∑ i = 1 m x ( i ) ( x ( i ) ) T ) W ) + ∑ i = 1 m ( x ( i ) ) T x ( i ) = − t r ( W T X X T W ) + ∑ i = 1 m ( x ( i ) ) T x ( i ) \sum^m_{i=1} \| \hat{x}^{(i)} - x^{(i)} \|^2_2 = \sum^m_{i=1} \| Wz^{(i)} - x^{(i)} \|^2_2 \\ = \sum^m_{i=1} \left( Wz^{(i)} \right)^T \left( Wz^{(i)} \right) - 2\sum^m_{i=1} \left( Wz^{(i)} \right)^T x^{(i)} + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = \sum^m_{i=1} \left( z^{(i)} \right)^T \left( z^{(i)} \right) - 2\sum^m_{i=1} \left( z^{(i)} \right)^T x^{(i)} + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = - \sum^m_{i=1} \left( z^{(i)} \right)^T \left( z^{(i)} \right) + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = -tr \left( W^T \left( \sum^m_{i=1} x^{(i)} \left( x^{(i)} \right)^T \right)W \right) + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = -tr \left( W^TXX^TW \right) + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} i=1∑m∥x^(i)−x(i)∥22=i=1∑m∥Wz(i)−x(i)∥22=i=1∑m(Wz(i))T(Wz(i))−2i=1∑m(Wz(i))Tx(i)+i=1∑m(x(i))Tx(i)=i=1∑m(z(i))T(z(i))−2i=1∑m(z(i))Tx(i)+i=1∑m(x(i))Tx(i)=−i=1∑m(z(i))T(z(i))+i=1∑m(x(i))Tx(i)=−tr(WT(i=1∑mx(i)(x(i))T)W)+i=1∑m(x(i))Tx(i)=−tr(WTXXTW)+i=1∑m(x(i))Tx(i)
在推导过程中,分别用到了 x ‾ ( i ) = W z ( i ) \overline{x}^{(i)} = Wz^{(i)} x(i)=Wz(i) ,矩阵转置公式 ( A B ) T = B T A T (AB)^T = B^TA^T (AB)T=BTAT, W T W = I W^TW = I WTW=I, z ( i ) = W T x ( i ) z^{(i)} = W^Tx^{(i)} z(i)=WTx(i) 以及矩阵的迹,最后两步是将代数和转为矩阵形式。
由于 W W W 的每一个向量 w j w_j wj 是标准正交基, ∑ i = 1 m x ( i ) ( x ( i ) ) T \sum^m_{i=1} x^{(i)} \left( x^{(i)} \right)^T ∑i=1mx(i)(x(i))T 是数据集的协方差矩阵, ∑ i = 1 m ( x ( i ) ) T x ( i ) \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} ∑i=1m(x(i))Tx(i) 是一个常量。最小化 ∑ i = 1 m ∥ x ^ ( i ) − x ( i ) ∥ 2 2 \sum^m_{i=1} \| \hat{x}^{(i)} - x^{(i)} \|^2_2 ∑i=1m∥x^(i)−x(i)∥22 又可等价于
arg min ⎵ W − t r ( W T X X T W ) s . t . W T W = I \underbrace{\arg \min}_W - tr \left( W^TXX^TW \right) s.t.W^TW = I W argmin−tr(WTXXTW)s.t.WTW=I
利用拉格朗日函数可得到
J ( W ) = − t r ( W T X X T W ) + λ ( W T W − I ) J(W) = -tr(W^TXX^TW) + \lambda(W^TW - I) J(W)=−tr(WTXXTW)+λ(WTW−I)
对 W W W 求导,可得 − X X T W + λ W = 0 -XX^TW + \lambda W = 0 −XXTW+λW=0 ,也即 X X T W = λ W XX^TW = \lambda W XXTW=λW 。 X X T XX^T XXT 是 n ′ n' n′ 个特征向量组成的矩阵, λ \lambda λ 为 X X T XX^T XXT 的特征值。 W W W 即为我们想要的矩阵。
对于原始数据,只需要 z ( i ) = W T X ( i ) z^{(i)} = W^TX^{(i)} z(i)=WTX(i) ,就可把原始数据集降维到最小投影距离的 n ′ n' n′ 维数据集。
基于最大投影方差的推导,这里就不再赘述,有兴趣的同仁可自行查阅资料。
PCA算法流程总结
输入: n n n 维样本集 D = ( x ( 1 ) , x ( 2 ) , . . . , x ( m ) ) D = \left( x^{(1)},x^{(2)},...,x^{(m)} \right) D=(x(1),x(2),...,x(m)) ,目标降维的维数 n ′ n' n′ 。
输出:降维后的新样本集 D ′ = ( z ( 1 ) , z ( 2 ) , . . . , z ( m ) ) D' = \left( z^{(1)},z^{(2)},...,z^{(m)} \right) D′=(z(1),z(2),...,z(m)) 。
主要步骤如下:
- 对所有的样本进行中心化, x ( i ) = x ( i ) − 1 m ∑ j = 1 m x ( j ) x^{(i)} = x^{(i)} - \frac{1}{m} \sum^m_{j=1} x^{(j)} x(i)=x(i)−m1∑j=1mx(j) 。
- 计算样本的协方差矩阵 X X T XX^T XXT 。
- 对协方差矩阵 X X T XX^T XXT 进行特征值分解。
- 取出最大的 n ′ n' n′ 个特征值对应的特征向量 { w 1 , w 2 , . . . , w n ′ } \{ w_1,w_2,...,w_{n'} \} {w1,w2,...,wn′} 。
- 标准化特征向量,得到特征向量矩阵 W W W 。
- 转化样本集中的每个样本 z ( i ) = W T x ( i ) z^{(i)} = W^T x^{(i)} z(i)=WTx(i) 。
- 得到输出矩阵 D ′ = ( z ( 1 ) , z ( 2 ) , . . . , z ( n ) ) D' = \left( z^{(1)},z^{(2)},...,z^{(n)} \right) D′=(z(1),z(2),...,z(n)) 。
注:在降维时,有时不明确目标维数,而是指定降维到的主成分比重阈值 k ( k ϵ ( 0 , 1 ] ) k(k \epsilon(0,1]) k(kϵ(0,1]) 。假设 n n n 个特征值为 λ 1 ⩾ λ 2 ⩾ . . . ⩾ λ n \lambda_1 \geqslant \lambda_2 \geqslant ... \geqslant \lambda_n λ1⩾λ2⩾...⩾λn ,则 n ′ n' n′ 可从 ∑ i = 1 n ′ λ i ⩾ k × ∑ i = 1 n λ i \sum^{n'}_{i=1} \lambda_i \geqslant k \times \sum^n_{i=1} \lambda_i ∑i=1n′λi⩾k×∑i=1nλi 得到。
PCA算法主要优缺点
| 优缺点 | 简要说明 |
|---|---|
| 优点 | 1. 仅仅需要以方差衡量信息量,不受数据集以外的因素影响。 2.各主成分之间正交,可消除原始数据成分间的相互影响的因素。3. 计算方法简单,主要运算是特征值分解,易于实现。 |
| 缺点 | 1.主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。2. 方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。 |
降维的必要性及目的
降维的必要性:
- 多重共线性和预测变量之间相互关联。多重共线性会导致解空间的不稳定,从而可能导致结果的不连贯。
- 高维空间本身具有稀疏性。一维正态分布有68%的值落于正负标准差之间,而在十维空间上只有2%。
- 过多的变量,对查找规律造成冗余麻烦。
- 仅在变量层面上分析可能会忽略变量之间的潜在联系。例如几个预测变量可能落入仅反映数据某一方面特征的一个组内。
降维的目的:
- 减少预测变量的个数。
- 确保这些变量是相互独立的。
- 提供一个框架来解释结果。相关特征,特别是重要特征更能在数据中明确的显示出来;如果只有两维或者三维的话,更便于可视化展示。
- 数据在低维下更容易处理、更容易使用。
- 去除数据噪声。
- 降低算法运算开销。
KPCA与PCA的区别
应用PCA算法前提是假设存在一个线性超平面,进而投影。那如果数据不是线性的呢?该怎么办?这时候就需要KPCA,数据集从 n n n 维映射到线性可分的高维 N > n N >n N>n,然后再从 N N N 维降维到一个低维度 n ′ ( n ′ < n < N ) n'(n'<n<N) n′(n′<n<N) 。
KPCA用到了核函数思想,使用了核函数的主成分分析一般称为核主成分分析(Kernelized PCA, 简称KPCA)。
假设高维空间数据由 n n n 维空间的数据通过映射 ϕ \phi ϕ 产生。
n n n 维空间的特征分解为:
∑ i = 1 m x ( i ) ( x ( i ) ) T W = λ W \sum^m_{i=1} x^{(i)} \left( x^{(i)} \right)^T W = \lambda W i=1∑mx(i)(x(i))TW=λW
其映射为
∑ i = 1 m ϕ ( x ( i ) ) ϕ ( x ( i ) ) T W = λ W \sum^m_{i=1} \phi \left( x^{(i)} \right) \phi \left( x^{(i)} \right)^T W = \lambda W i=1∑mϕ(x(i))ϕ(x(i))TW=λW
通过在高维空间进行协方差矩阵的特征值分解,然后用和PCA一样的方法进行降维。由于KPCA需要核函数的运算,因此它的计算量要比PCA大很多。