从零开始-Machine Learning学习笔记(25)-集成学习
文章目录
- 1. Boosting - AdaBoosting
- 2. Bagging与随机森林
- 2.1 Bagging - 并行式集成学习
- 2.2 随机森林
- 3. 结合策略
- 3.1 平均法
- 3.2 投票法
- 3.3 学习法 - Stacking
- 4. 多样性增强
集成学习(ensemble learning)通过构建并结合多个学习器来完成学习任务,有时也被称为多分类器系统(multi-classifier system) 、基于委员会的学习(committee-based learning)等。
根据个体学习器的生成方式,目前的集成学习方法大致可分为两大类,即个体学习器问存在强依赖关系、必须串行生成的序列化方法?以及个体学习器间不存在强依赖关系、可同时生成的并行化方法;前者的代表是Boosting ,后者的代表是Bagging 和"随机森林" (Random Forest)。
1. Boosting - AdaBoosting
Boosting 是一族可将弱学习器提升为强学习器的算法.这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值T,最终将这T个基学习器进行加权结合。
AdaBoosting是Boosting族算法最为著名的代表,其比较容易的理解是基于“加行模型”,即基学习器的线性组合:
H ( x ) = ∑ t = 1 T α t h t ( x ) H(x) = \sum_{t=1}^{T}\alpha_th_t (x) H(x)=t=1∑Tαtht(x)
来最小化指数损失函数:
L e x p ( H ∣ D ) = E x D [ e − f ( x ) H ( x ) ] L_{exp} (H|D) = E_{x~D}[e^{-f(x)H(x)}] Lexp(H∣D)=Ex D[e−f(x)H(x)]
其中,算法过程第三行 h t = L ( D , D t ) h_t=L(D, D_t) ht=L(D,Dt)表示基于分布 D t D_t Dt从数据集D中训练出分类器 h t h_t ht;算法过程第四行为估计 h t h_t ht的误差; α t = 1 2 l n ( 1 − ξ t ξ t ) \alpha_t=\frac{1}{2}ln(\frac{1-\xi_t}{\xi_t}) αt=21ln(ξt1−ξt)为分类器 h t h_t ht的权重,Zt是规范化因子。
在AdaBoost算法中,第一个基分类器 h 1 h_1 h1是通过直接将基学习算法用于初始数据分布而得;此后迭代地生成 h t h_t ht和 α t α_t αt,当基分类器 h t h_t ht基于分布 Ð t Ð_t Ðt产生后,该基分类器的权重 α t α_t αt应使得 α t h t α_th_t αtht最小化指数损失函数:
l e x p ( α t h t ∣ D t ) = E x D t [ e − f ( x ) α t h t ] = e − α t ( 1 − ξ t ) + e α t ξ t l_{exp}(\alpha_t h_t|D_t) = E_{x~D_t}[e^{-f(x)\alpha_t h_t}]\\ = e^{-\alpha_t}(1-\xi_t)+e^{\alpha_t}\xi_t lexp(αtht∣Dt)=Ex Dt[e−f(x)αtht]=e−αt(1−ξt)+eαtξt
上式对 α t \alpha_t αt求偏导并等于零有:
∂ l e x p ( α t h t ∣ D t ) ∂ α t = − e − α t ( 1 − ξ t ) + e α t ξ t = 0 \frac{\partial l_{exp}(\alpha_t h_t|D_t)}{\partial \alpha_t} = -e^{-\alpha_t}(1-\xi_t)+e^{\alpha_t}\xi_t = 0 ∂αt∂lexp(αtht∣Dt)=−e−αt(1−ξt)+eαtξt=0
可以求得 α t \alpha_t αt:
α t = 1 2 l n ( 1 − ξ t ξ t ) \alpha_t=\frac{1}{2}ln(\frac{1-\xi_t}{\xi_t}) αt=21ln(ξt1−ξt)
这就是第6行的权重更新公式。
算法第7行中的样本分布更新公式的推导我在这里就直接贴出书上推导过程:
根据推导,我们可以知道算法第7行中的Zt为:
Z ( t ) = E x − D [ e − f ( x ) H t ( x ) ] E x − D [ e − f ( x ) H t − 1 ( x ) ] = 本 轮 指 数 损 失 函 数 值 上 一 轮 迭 代 的 指 数 损 失 函 数 值 Z(t) = \frac{E_{x-D}[e^{-f(x)H_t(x)}]} {E_{x-D}[e^{-f(x)H_{t-1}(x)}]}=\frac{本轮指数损失函数值}{上一轮迭代的指数损失函数值} Z(t)=Ex−D[e−f(x)Ht−1(x)]Ex−D[e−f(x)Ht(x)]=上一轮迭代的指数损失函数值本轮指数损失函数值
Boosting其实就是在每一轮的迭代中,为每个训练样本赋予一个权值,这叫**“重赋权法”(re-weighting);对于那些无法接受带权样本的算法,可以采用“重采样法”(re-sampling)**来处理。
从偏差一方差分解的角度看, Boosting 主要关住降低偏差,因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成。
2. Bagging与随机森林
2.1 Bagging - 并行式集成学习
Bagging基于**“自助采样法”(bootstrap sampling)**,即有放回的采样,同一个样本可能会被多次访问到,每次采样我们都可以得到含m个样本的采样集,其中m就是原训练集的大小。基于每次采样,都可以训练一个基学习器,再将这些基学习器进行结合。
对于分类问题: 采用投票法
对于回归问题: 采用平均法
其算法流程如下:
从偏差方差分解的角度看, Bagging 主要关注降低方差,因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显。
2.2 随机森林
RF在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机属性选择。具体来说,传统决策树在选择划分属性时是在当前结点的属性集合(假定有d个属性)中选择一个最优属性;而在RF中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k( k ≤ d k \leq d k≤d)个属性的子集,然后再从这个子集中选择一个最优属性用于划分。其中k控制了随机性的引入程度,一般推荐k的取值为:
k = l o g 2 d k = log_2d k=log2d
随机森林简单、容易实现、计算开销小,令人惊奇的是, 它在很多现实任务中展现出强大的性能,被誉为"代表集成学习技术水平的方法"可以看出,随机森林对Bagging 只做了小改动, 但是与Bagging 中基学习器的"多样性"仅通过样本扰动(通过对初始训练集采样)而来不同,随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,这就使得最终集成的泛化性能可通过个体学习器之间差异度的增加而进一步提升。
3. 结合策略
3.1 平均法
简单平均法:
H ( x ) = 1 T ∑ i = 1 T h i ( x ) H(x) = \frac{1}{T}\sum_{i=1}^{T}h_i(x) H(x)=T1i=1∑Thi(x)
加权平均法:
H ( x ) = ∑ i = 1 T w i h i ( x ) H(x) = \sum_{i=1}^{T}w_ih_i(x) H(x)=i=1∑Twihi(x)
3.2 投票法
绝大多数投票法: 若某标记得票过半数,则预测为该标记;否则拒绝预测。
相对多数投票法: 即预测为得票最多的标记,若同时有多个标记获最高票,则从中随机选取一个。
加权投票法: 与加权平均法类似,给每个标记的结果进行加权。
3.3 学习法 - Stacking
Stacking 先从初始数据集训练出初级学习器,然后"生成"一个新数据集用于训练次级学习器。在这个新数据集中,初级学习器的输出被当作样例输入特征,而初始样本的标记仍被当作样例标记。
简而言之:Stacking就是把初级学习器的输出(预测结果)作为次级学习器的特征,然后来训练次级学习器。
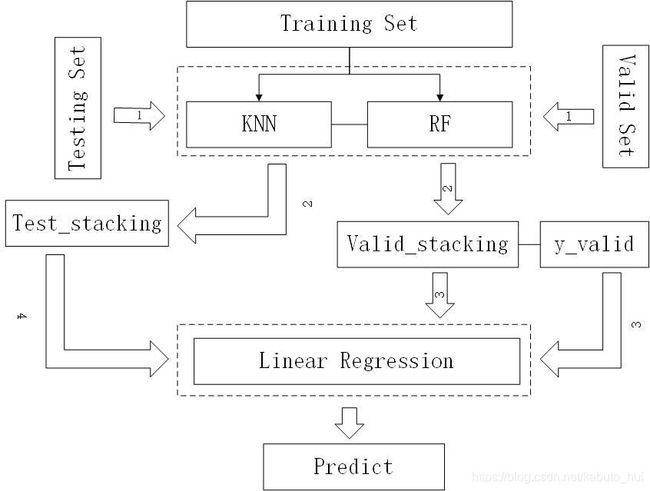
我以KNN,RF作为初级学习器,LR为次级学习器,画了如下的图来作为说明:
- 训练集先训练KNN和RF;
- 测试集和验证集分别进入KNN和RF模型,会得到两种输出结果,将其结合起来就得到了Test_Stacking和Valid_Stacking;
- 使用
作为新的训练集训练次级学习器LR; - 将Test_Stacking输入到LR模型中,就得到了Test所需要的预测结果。
4. 多样性增强
在集成学习中需有效地生成多样性大的个体学习器. 与简单地直接用初始数据训练出个体学习器相比,如何增强多样性呢?一般思路是在学习过程中引入随机性,常见做法主要是对数据样本、输入属性、输出表示、算法参数进行扰动:
数据样本扰动: 数据样本扰动通常是基于采样法,例如在Bagging中使用自助采样,在AdaBoost中使用序列采样。常用于“不稳定基学习器”如如决策树、神经网络等。
输入属性扰动: 法从初始属性集中抽取出若干个属性子集,再基于每个属性子集训练一个基学习器。适用于包含大量冗余属性的数据,在子空间中训练个体学习器不仅能产生多样性大的个体,还会因属性数的减少而大幅节省时间开销,同时,由于冗余属性多,减少一些属性后训练出的个体学习器也不至于太差。
输出表示扰动: 此类做法的基本思路是对输出表示进行操纵以增强多样性.可对训练样本的类标记稍作变动,如"翻转法" (Flipping Output) [Breiman, 2000] 随机改变一些训练样本的标记;也可对输出表示进行转化,如"输出调制法" (Output Smearing) [Breiman, 2000] 将分类输出转化为回归输出后构建个体学习器;还可将原任务拆解为多个可同时求解的子任务,如ECOC[Dietterich andBakiri, 1995] 利用纠错输出码将多分类任务拆解为一系列二分类任务来训练基学习器。
算法参数扰动: 基学习算法一般都有参数需进行设置,例如神经网络的隐层神经元数、初始连接权值等,通过随机设置不同的参数,往往可产生差别较大的个体学习器。对参数较少的算法,可通过将其学习过程中某些环节用其他类似方式代替,从而达到扰动的目的。