David Silver强化学习课程笔记（八）（下）

第八课（下）：基于Simulation的搜索方法

        在《第八课（上）：学习与规划的结合》中，我们讲到了Model-Based RL方法，在该方法中，我们首先拟合得到一个模型，然后可以利用各种规划方法进行规划，或者，可以引申出Sample-Based Planning，也即我们并不是去采用贝尔曼方程计算，而是用模型进行采样，然后利用Model-Free方法进行学习。本文中要讲的Simulation-Based Search与Sample-Based Planning有着异曲同工之妙，值得注意的是，这里的Simulation-Based Search仍然是一种结合Model-Free RL与Model-Based RL的强化学习方法。

        首先，我们来理解一下，什么是Simulation-Based Search？两大要素，一是simulation，一是search。

        simulation指的是用模型去采样，不过这些样本有一个共同点，就是从同一个状态开始转移，这与Sample-Based Planning是不一样的。从前面的AB Example中可以看出来我们是从随机初始化状态开始进行采样的，因为最终我们需要计算V(A)、V(B)，如果仅仅从B开始转移，那么我们甚至得不到对于V(A)的估计，所以是片面的。当我们从同一个状态s开始进行了N次实验之后，我们就可以将其连成一棵以s为根节点的树，用于search。

        search从字面意义来讲，就是搜索，在simulation中，我们构建了一棵以当前状态为根节点的树，并由此选择动作的过程便叫做search。

        先来看看前向搜索（Forward Search）。前向搜索算法通过lookahead来选择最好的动作，这里所谓的lookahead表示从当前节点开始完全扩展，换句话说，所有情形都在里面。这种算法有一个优点：我们不用去求解整个MDP，只需要求解部分MDP(sub-MDP)即可，或者说，我们不需要对所有状态求得最优策略，而只要对当前状态求得最优策略。Forward Search示意图如下：

        如果我们对此引入Simulation，则得到Simulation-Based Search，这样我们就不用构建完整的树了，而只需要从样本中学习：

        这种方法表述如下：

        后面我们将分别对Monte-Carlo Seach和TD search进行介绍。

Monte-Carlo Simulation/Search

        我们知道，所谓Monte-Carlo方法， 是指“当所求解的问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解”。我们能够很容易地想出Monte-Carlo Simulation算法以及Monte-Carlo Search算法：

        其中，估计V(s)只是叫做Simulation，而估计Q(s, a)才能叫做Search，因为我们前面说到search表示去寻找并选择最优动作的过程。如果将Monte-Carlo Search中的最后一步，也即选择real action的那一步去掉不看，那么这个算法可以看作是一个策略估计（policy evaluation）算法。需要注意的是，这里估计的策略是simulation policy，而不是real policy，real policy是最后一步得到的贪婪策略。好了，既然说到了策略估计，那我们就会想，是不是有个策略改善（policy improvement）呢？对，没错，显然我们需要对simulation policy进行改进，不然我们的real policy肯定也不咋地。比如说，假设模型是正确或者近似正确的，那么这个模型就可以被近似看做真实环境，如果我们采取的simulation policy慢慢地改进，变得越来越倾向于选择return较高的动作，则Q(s, a)也将由对于较差动作的估计变为对于较好动作的估计，比如一开始可能simulation policy里面没有较高return的action，那么Q中也就没有对这个action的估计，最后的real policy便不可能包括这个较高return的action。所以，对于simulation policy的改进最终将使得我们的real policy得到改进。下面给出Evaluation以及Improve（Simulation）的PPT：

        总结Evaluation：在仿真中从现在（real）的状态开始，simulate K episodes（用simulation policy），用这些样本构造搜索树，并估计Q(s, a)，选择real action来控制real agent，注意这里没有探索，是确定性策略。

        总结Simulation：这页主要将improve，其中在simulation时有两种策略，当我们遇到没有见过的状态时，使用default policy，而遇到见过的策略时，则使用tree policy。我们会对tree policy进行改进，并且，得到的策略是epsilon-greedy策略，也即随机性策略。这种方法是有收敛性保证的，Q(s, a)将收敛到最优动作值函数，因而real policy将收敛到最优策略。

        将Evaluation与Improve（Simulation）相结合，可以得到完整的蒙特卡罗树搜索算法（MCTS），也就是大名鼎鼎的AlphaGo中用到的核心算法。下面以围棋为例介绍树的构造过程：

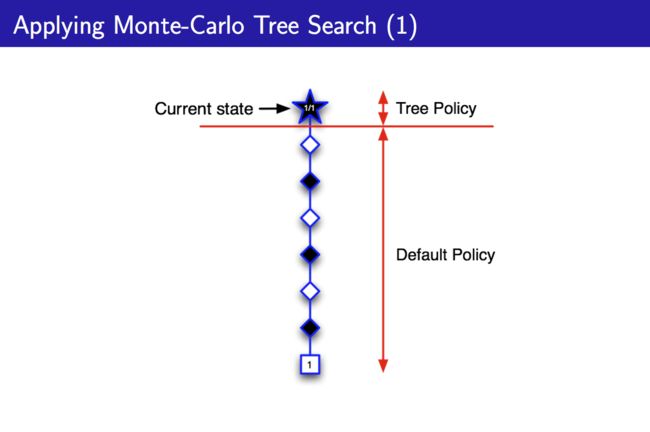
        PPT中讲的是V(s)的估计，也即这里考虑的是我（黑子）当前在状态s，选择一个策略，使得值函数V(s)最大，所以说是考虑某个状态s究竟有多好。不过由于我们是self-play，所以也要为对手（白子）选择最优策略。选择先在“脑子”里面simulate一个episode：

        图中1/1表示下了一盘棋，并且己方（黑子）赢了，且一开始没有见过除了Current State之外的状态，所以均采用Default Policy。图中的白色块表示白子落子，虽然对于白子而言是利用某个策略来选择动作，但对于黑子而言可以当做一个状态。此时，我们见到了Current state下面的那个白色块表示的状态，所以将其加入到Tree Policy中，继续运行算法：

        此时因为只有Tree Policy中只有一个白色块选择，所以就直接选这个作为后续状态，但是这个episode却不像上一步中尝试该状态时那样顺利，这次我（黑子）输了，于是我对这个状态的评估进行更新，在Tree Policy中将其值函数置为0，不再选用这个状态。由于Tree Policy是epsilon greedy的，所以可以到达另外的状态：

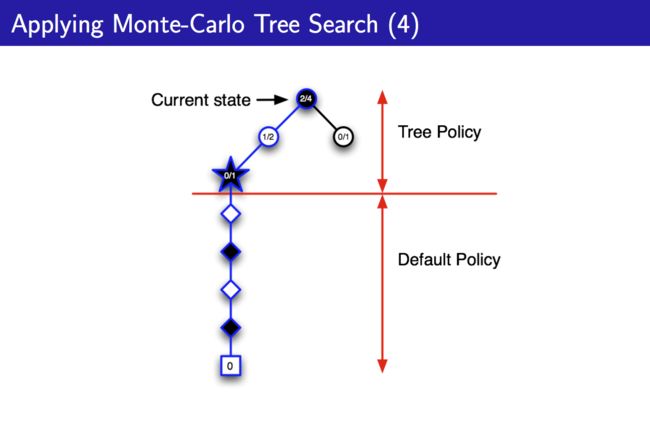
        该状态的simulation表明，我（黑子）赢了，所以继续选择这一白色块状态，并往下搜索，将该白色块后续的黑色块加入Tree Policy中：

        对这个黑色块进行simulation，发现输了，置其值函数为0，然后寻找另一个状态：

        依此类推，得到一个Tree Policy，用于对Current state进行决策。总的来说，这种方法就是将整个对局放在心中，不过一般是一步一步来，走一步a，到s，再按照上述步骤建树，这就是MCTS。这种算法的优点为：

        其中较为值得注意的是，“动态扩展树”，只评估现在的状态。

        说了这么久，说的是MC Search，下面我们介绍TD Search。

        TD Search也是一种Simulation-Based Search方法，与MC Search不同的是，这种方法使用TD代替了MC，有着bootstrapping的特点。在MCTS中我们从当前开始对于sub-MDP应用MC control，而TD Search则是从当前开始对sub-MDP应用Sarsa。可见，在TD Search中，每个simulation episode中都将一直更新，而不是episode结束才更新：

        搜索树与值函数估计方法的联系：

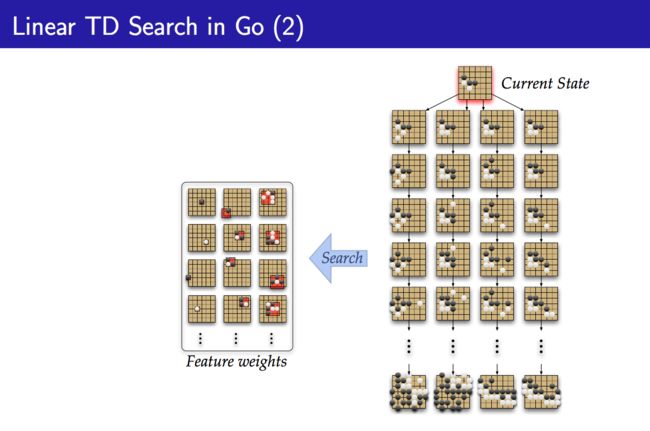
        这张PPT表明，Search Tree使用的是查找表的估计方法，但与一般的model-free强化学习不同，因为它是simulation-based search，所以会稍微不那么naive，不过对于一个较大的搜索空间，值函数估计还是必要的。由此，PPT引出了Linear TD Search：

        采用线性值函数估计器代替查找表估计方法，从而使之能够处理较大的搜索空间。

        上一篇文章中我们讲过了Dyna结构，该结构的想法是，我们不仅仅可以从real experience中学习，我们还可以利用simulation来促进学习。Dyna-2结构的核心想法也很类似，这里我们考查Dyna-2结构：

        在这种结构中，我们的智能体维持了两组权重，一组处理Long-term memory，一组处理Short-term memory（working memory）。其中Long-term memory用real experience进行更新，而Short用simulated experience进行更新，因为长期记忆一般是普适性的，所以要求比较准确，而短期记忆用于即时决策，所以用当前状态通过simulation构建得到的搜索树来进行决策。由于一组权重对应一个值函数，所以在Dyna-2中我们有两个值函数，利用real experience对应的值函数V1(s)告诉我们在实际场景中，我们所预估的期望回报，而simulated experience对应的值函数V2(s)则是从搜索树中估计得到的预期回报，这是短期的。假设我们在攀岩，那么V1(s)表明，根据以往攀岩的经历（real experience），我们当前的这个位置（某条路线上的一个点）将会触发较高的期望回报，从而给我们一个大局观；而V2(s)通过simulate后面的路线（或者说放手的位置），发现这块石头松了，不能借力，那块石头很牢固，从而给我们一个后续行为的局部引导。最终，我们的值函数是这两个值函数的和。

        给出Dyna-2结构的Linear TD算法如下：

        在上面4张PPT中，前两张表示从real experience中学习Long-term memory，而后两张表示从simulated experience中学习Short-term memory，从示例图中可以看出，Long-term memory学的是大局观，是从真实（real）的以往的经验中学到（learning）的，要长期记住（long-term）的东西，而Short-term memory学的是后续行为的局部引导，或者说是具体实施细节，是从虚拟（simulated）的当前（构想）的经验（或者说是样本更确切，因为说经验总像是real experience一样）搜索（search）得来的东西。整理这句话如下：

        Long-term memory学的是大局观，是从真实的以往的经验中学到的，要长期记住的东西，而Short-term memory学的是后续行为的局部引导，或者说是具体实施细节，是从虚拟的当前（构想）的经验中搜索得来的东西。

        好了，时间也不早了，本文就聊到这里，周末愉快~