CS231n 2019 Spring

这份笔记和我结合知乎智能单元，以及B站同济子豪兄的2019年cs231n讲解视频整理完成的。大部分内容引自知乎智能单元，在此感谢智能单元的翻译者和B站同济子豪兄。

在笔记中有部分知识点笔者没有完全理解，就先按笔者的理解程度记下来来了。具体查看文章最后的注脚。

1 计算机视觉发展历史

2 图像分类的流程与KNN算法

图像分类的目标：这一节我们将介绍图像分类问题。所谓图像分类问题，就是已有固定的分类标签集合，然后对于输入的图像，从分类标签集合中找出一个分类标签，最后把分类标签分配给该输入图像。虽然看起来挺简单的，但这可是计算机视觉领域的核心问题之一，并且有着各种各样的实际应用。在后面的课程中，我们可以看到计算机视觉领域中很多看似不同的问题（比如物体检测和分割），都可以被归结为图像分类问题。

图像分类的例子： 以下图为例，图像分类模型读取该图片，并生成该图片属于集合 {cat, dog, hat, mug}中各个标签的概率。需要注意的是，对于计算机来说，图像是一个由数字组成的巨大的3维数组。在这个例子中，猫的图像大小是宽800像素，高600像素，有3个颜色通道，分别是红、绿和蓝（简称RGB）。如此，该图像就包含了800X600X3=1440000个数字，每个数字都是在范围0-255之间的整型，其中0表示全黑，255表示全白。我们的任务就是把这些上百万的数字变成一个简单的标签，比如"猫"。(为什么是0-255之间的整数呢？因为我们用8个比特8 bit 来存储一个像素值)

图像分类的任务，就是对于一个给定的图像，预测它属于的那个分类标签（或者给出属于一系列不同标签的可能性）。图像是3维数组，数组元素是取值范围从0到255的整数。数组的尺寸是宽度x高度x3，其中这个3代表的是红、绿和蓝3个颜色通道。

图像分类问题的困难和挑战： 对于人来说，识别出一个像"猫"一样视觉概念是简单至极的，然而从计算机视觉算法的角度来看就值得深思了。我们在下面列举了计算机视觉算法在图像识别方面遇到的一些困难，要记住图像是以3维数组来表示的，数组中的元素是亮度值。

• 视角变化（Viewpoint variation）：同一个物体，摄像机可以从多个角度来展现。

• 大小变化（Scale variation）：物体可视的大小通常是会变化的（不仅是在图片中，在真实世界中大小也是变化的）。

• 形变（Deformation）：很多东西的形状并非一成不变，会有很大变化。（猫是液体…)

• 遮挡（Occlusion）：目标物体可能被挡住。有时候只有物体的一小部分（可以小到几个像素）是可见的。

• 光照条件（Illumination conditions）：在像素层面上，光照的影响非常大。

• 背景干扰（Background clutter）：物体可能混入背景之中，使之难以被辨认。

• 类内差异（Intra-class variation）：一类物体的个体之间的外形差异很大，比如椅子。这一类物体有许多不同的对象，每个都有自己的外形。

2-1 数据驱动分类器的提出

与传统的分类算法不同，我们不可能用手工编写一个程序去识别图像是否表示猫。曾经有人尝试过用边缘检测的方式提取出猫的边缘信息，但是这种方法太麻烦而且对于分类问题的解决太过针对性。假设我们将猫换成马，那是不是又要写一个提取马的边缘检测并分类的程序呢？这样的操作过于麻烦，于是就有人提出了数据驱动的方法。

数据驱动方法：如何写一个图像分类的算法呢？这和写个排序算法可是大不一样。怎么写一个从图像中认出猫的算法？搞不清楚。因此，与其在代码中直接写明各类物体到底看起来是什么样的，倒不如说我们采取的方法和教小孩儿看图识物类似：给计算机很多数据，然后实现学习算法，让计算机学习到每个类的外形。这种方法，就是_数据驱动方法_。既然该方法的第一步就是收集已经做好分类标注的图片来作为训练集，那么下面就看看数据库到底长什么样：

机器学习：图像驱动分类器的流程

• 训练集的获取：获得大量的图片和与图片对应的标签
• 训练学习：利用机器学习模型在大量数据集的基础上训练得到一个分类器
• 测试集评估：让分类器来预测它未曾见过的图像的分类标签，并以此来评价分类器的效果。我们会将分类器预测的标签和图像真正的分类标签进行对比，来评估分类器的分类效果。

2-2 NN分类器（Nearest Neighbor分类器）

NN分类器是KNN分类器的一个特殊形式，即NN分类器是K=1的KNN分类器。

CIFAR10 图像分类数据集：这个数据集包含了10种类别的标签。训练集中有5万张图片，测试集中有10万张图片。每张图片都是32px*32px的3通道彩色图片。

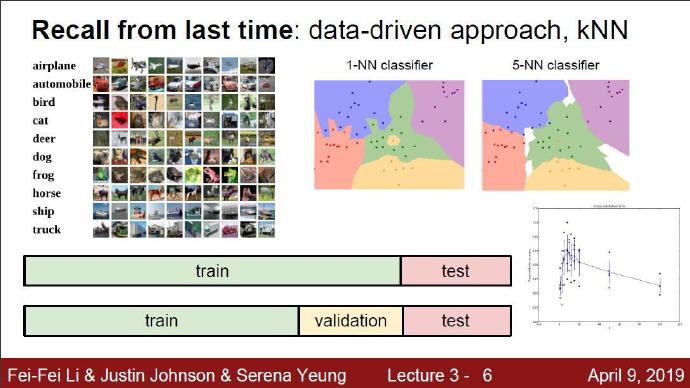
KNN算法在CIFAR10数据集上的运用： 上图左侧是带有正确标签的训练集，右侧是用KNN进行图片分类的过程。右侧第一列是待分类的图片，右侧箭头指向的那一行图片就是待分类图片在训练集中根据像素差找到的最相似的10个图片。这里取了10张图片，也就是说KNN算法在这里的K取值为10。这10张图片由多种类别的图像组成，但是在分类器看来都与待分类图片很相似。于是我们下一步就要在这10张图片看哪一种类别最多，那种分类就是KNN算法给待分类图片的判定结果。

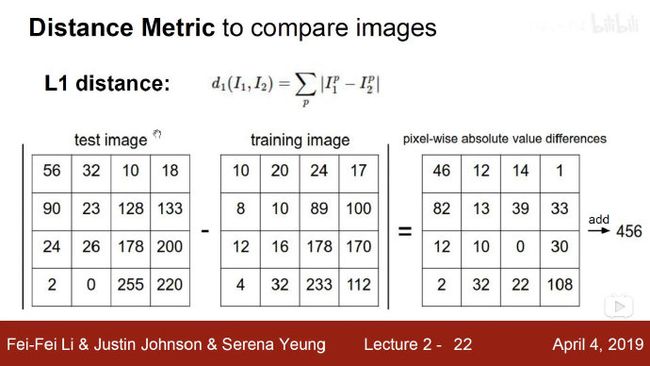
2-2-2 L1距离（曼哈顿距离）

那么问题来了，KNN是如何找到与待测图片相似的图片呢？（即如何找到K个近邻的单位）最简单的方法就是求L1距离。

L1距离：又称出租车几何或曼哈顿距离。

本例子用KNN算法设定距离为L1，找出训练集中与待分类图片相似的图片。过程如下：在像素大小为32*32的图片中，取测试图片和训练图片对应像素块值做差再加上绝对值。再将这32个像素块差的绝对值差求和，得到L1距离。只对图像的每个像素做对比，对应像素相减取绝对值，再将这些差值相加就是距离。如果两张图片一模一样，那么L1距离为0，但是如果两张图片很是不同，那L1值将会非常大。

下面，让我们看看如何用代码来实现这个分类器。首先，我们将CIFAR-10的数据加载到内存中，并分成4个数组：训练数据和标签，测试数据和标签。在下面的代码中， Xtr（大小是50000x32x32x3）存有训练集中所有的图像，Ytr 是对应的长度为50000的1维数组，存有图像对应的分类标签（从0到9）：

Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # a magic function we provide
# flatten out all images to be one-dimensional
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000 x 3072

现在我们得到所有的图像数据，并且把他们拉长成为行向量了。接下来展示如何训练并评价一个分类器：

nn = NearestNeighbor() # create a Nearest Neighbor classifier class
nn.train(Xtr_rows, Ytr) # train the classifier on the training images and labels
Yte_predict = nn.predict(Xte_rows) # predict labels on the test images
# and now print the classification accuracy, which is the average number
# of examples that are correctly predicted (i.e. label matches)
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )

作为评价标准，我们常常使用准确率，它描述了我们预测正确的得分。请注意以后我们实现的所有分类器都需要有这个API: train (X, y) 函数。该函数使用训练集的数据和标签来进行训练。从其内部来看，类应该实现一些关于标签和标签如何被预测的模型。这里还有个 predict(X) 函数，它的作用是预测输入的新数据的分类标签。现在还没介绍分类器的实现，下面就是使用L1距离的Nearest Neighbor分类器的实现方式是：

最近邻分类器的实现：

import numpy as np

class NearestNeighbor(object):
	def __init__(self):
		pass

##记忆训练数据
def train(self, X, y):
""" X is N x D where each row is an example. Y is 1-dimension of size N """
# the nearest neighbor classifier simply remembers all the training data
	self.Xtr = X
	self.ytr = y
def predict(self, X):
	""" X is N x D where each row is an example we wish to predict label for """
	num_test = X.shape[0]
	# lets make sure that the output type matches the input type
	Ypred = np.zeros(num_test, dtype = self.ytr.dtype)


##对于每个测试图像：查找最近的训练图像，预测最近图像的标签。
# loop over all test rows
for i in xrange(num_test):
	# find the nearest training image to the i'th test image
	# using the L1 distance (sum of absolute value differences)
	distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
	min_index = np.argmin(distances) # get the index with smallest distance
	Ypred[i] = self.ytr[min_index] # predict the label of the nearest example
    
return Ypred

如果你用这段代码跑CIFAR-10，你会发现准确率能达到38.6%。这比随机猜测的10%要好，但是比人类识别的水平（[据研究推测是94%]）和卷积神经网络能达到的95%还是差多了。

2-2-3 L2距离（欧式距离）

计算向量间的距离有很多种方法，另一个常用的方法是L2距离（欧式距离）。从几何学的角度，可以理解为它在计算两个向量间的欧式距离。L2距离的计算公式如下： $d_2(I_1,I_2)=\sqrt{{\sum }_p(I_1^p-I_2^p{)}^2}$

换句话说，我们依旧是在计算图片像素间的差值，只是先求其差值的平方，然后把这些像素差值的平方全部加起来求和，最后对这个和开方。在Numpy中，我们只需要替换上面代码中的1行代码就行：

distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))

注意在这里使用了np.sqrt，但是在实际中可能不必多此一举。因为求平方根函数是一个_单调函数_，它对不同距离的绝对值求平方根虽然改变了数值大小，但依然保持了不同距离大小的顺序。所以用不用它，都能够对像素差异的大小进行正确比较。如果你在CIFAR-10上面跑这个模型，正确率是35.4%，比刚才低了一点。

L1和L2比较。比较这两个度量方式是挺有意思的。在面对两个向量之间的差异时，L2比L1更加不能容忍这些差异。也就是说，相对于1个巨大的差异，L2距离更倾向于接受多个中等程度的差异。L1和L2都是在[p-norm]常用的特殊形式。

2-3 KNN分类器

KNN算法: 给定一个待分类样本，在特征空间中找k个与样本最相似(即特征空间中最邻近)的数据。如果这K个相似数据中的大多数属于某一个类别，则该样本也属于这个类别。其中K通常是不大于20的整数。KNN算法中，所选择的相似样本都是已经正确分类的对象。该方法在分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。（换一个简单的说法，如果要判定你是不是个好人？用KNN算法来判别的话，就是去找你身边K个好朋友，看那K个好朋友是好人还是坏人。如果K个朋友是大多数是好人，那么大概率你也是好人。）

我们在上面用到的NN分类器设定的K为1，即只用最相似的1张图片的标签来作为测试图像的标签。这样的做法分类得到的结果准确度较低。我们如果使用k-Nearest Neighbor分类器就能做得更好。它的思想很简单：与其只找最相近的那1个图片的标签，我们找最相似的k个图片的标签，然后让他们针对测试图片进行投票，最后把票数最高的标签作为对测试图片的预测。所以当k=1的时候，k-Nearest Neighbor分类器就是Nearest Neighbor分类器。从直观感受上就可以看到，更高的k值可以让分类的效果更平滑，使得分类器对于异常值处理效果更好。

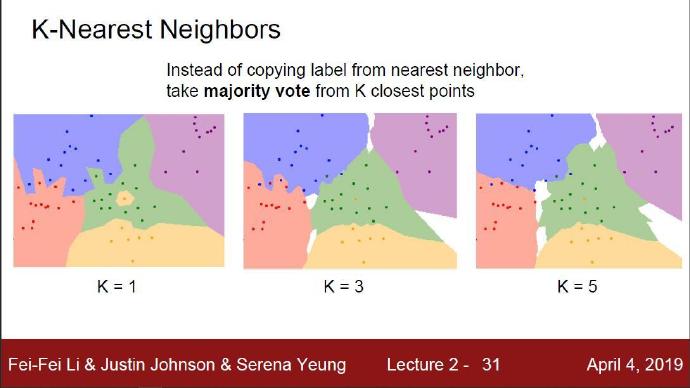
上面示例展示了Nearest Neighbor分类器和5-Nearest Neighbor分类器的区别。例子使用了2维平面内的点来表示，分成3种（红、蓝和绿）。不同颜色区域代表的是使用L2距离的分类器的 决策边界 （决策边界是不同分类点之间的垂直平分线）。白色的区域是分类模糊的例子（即图像与两个以上的分类标签有关联绑定）。需要注意的是，在NN分类器中，异常的数据点（比如：在蓝色区域中的绿点）制造出一个不正确预测的孤岛。5-NN分类器将这些不规则都平滑了，使得它针对测试数据的**泛化（generalization）**能力更好（例子中未展示）。注意，5-NN中也存在一些灰色区域，这些区域是因为近邻标签的最高票数相同导致的（比如：2个邻居是红色，2个邻居是蓝色，还有1个是绿色）。

在实际中，大多使用k-NN分类器。但是k值和距离的选取如何确定呢？接下来就讨论这个问题。

2-4 用于超参数调优的验证集

k-NN分类器需要设定k值，那么选择k值为多少最合适的呢？距离的选择上又有哪些呢？比如L1距离函数和L2距离函数等。那么选哪个距离比较好呢？还有不少选择我们甚至都没有考虑到（比如：点积）。所有这些选择，被称为超参数（hyperparameter）。在基于数据进行学习的机器学习算法设计中，超参数是很常见的。一般说来，这些超参数具体怎么设置或取值并不是显而易见的。

2-4-1 验证集的提出

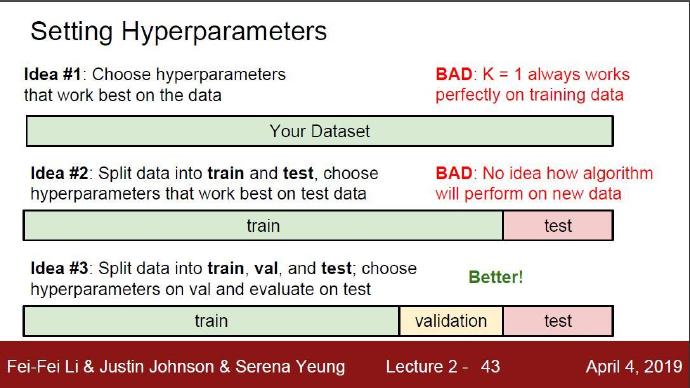
你可能会建议尝试不同的值，看哪个值表现最好就选哪个。好主意！我们就是这么做的，但这样做的时候要非常细心。特别注意：决不能使用测试集来进行调优。当你在设计机器学习算法的时候，应该把测试集看做非常珍贵的资源，不到最后一步，绝不使用它。如果你使用测试集来调优，而且算法看起来效果不错，那么真正的危险在于：算法实际部署后，性能可能会远低于预期。这种情况，称之为算法对测试集过拟合。

从另一个角度来说，如果使用测试集来调优，实际上就是把测试集当做训练集，由测试集训练出来的算法再跑测试集，自然性能看起来会很好。这其实是过于乐观了，实际部署起来效果就会差很多。所以，最终测试的时候再使用测试集，可以很好地近似度量你所设计的分类器的泛化性能（在接下来的课程中会有很多关于泛化性能的讨论）。

测试集数据在整个流程中只能使用一次。即只能在模型训练完成后，对最终的模型进行评价时才能使用测试集。

其实我们有不用测试集就能完成超参数调优的方法。其思路是：从训练集中取出一部分数据用来调优，我们称这部分数据为验证集（validation set）。以CIFAR-10为例，训练集总数是50000份，我们可以用49000个图像作为训练集，用1000个图像作为验证集。验证集其实就是作为假的测试集来调优。

下面就是代码：

 # assume we have Xtr_rows, Ytr, Xte_rows, Yte as before
    # recall Xtr_rows is 50,000 x 3072 matrix
    Xval_rows = Xtr_rows[:1000, :] # take first 1000 for validation
    Yval = Ytr[:1000]
    Xtr_rows = Xtr_rows[1000:, :] # keep last 49,000 for train
    Ytr = Ytr[1000:]
    
    # find hyperparameters that work best on the validation set
    validation_accuracies = []
    for k in [1, 3, 5, 10, 20, 50, 100]:
    
      # use a particular value of k and evaluation on validation data
      nn = NearestNeighbor()
      nn.train(Xtr_rows, Ytr)
      # here we assume a modified NearestNeighbor class that can take a k as input
      Yval_predict = nn.predict(Xval_rows, k = k)
      acc = np.mean(Yval_predict == Yval)
      print 'accuracy: %f' % (acc,)
    
      # keep track of what works on the validation set
      validation_accuracies.append((k, acc))

程序结束后，我们会作图分析出哪个k值表现最好，然后用这个k值来跑真正的测试集，并作出对算法的评价。

把训练集分成训练集和验证集。使用验证集来对所有超参数调优。最后只在测试集上跑一次并报告结果。

2-4-2 交叉验证方法的提出

交叉验证： 有时候，训练集数量较小（因此验证集的数量更小），人们会使用更为复杂的交叉验证的方法。将数据集A随机分为k个包，每次将其中一个包作为测试集，剩下k-1个包作为训练集进行训练。交叉验证方法提高了模型的准确性，避免了偶然误差。

还是用刚才的例子，如果使用交叉验证集，我们就不是取1000个图像作为验证集，而是将训练集平均分成5份，其中4份用来做训练集，1份用来验证集。然后我们循环着取其中4份来训练，其中1份来验证，最后取所有5次验证结果的平均值作为算法验证结果。这里将数据划分为5份，就称为五折交叉验证。

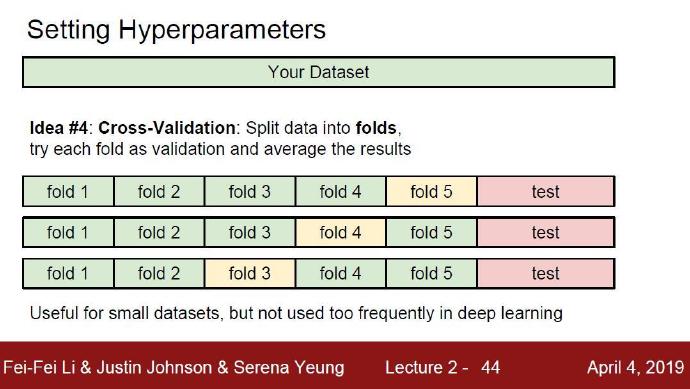
下面我们来看看五折交叉验证对于超参数K值的调优情况：

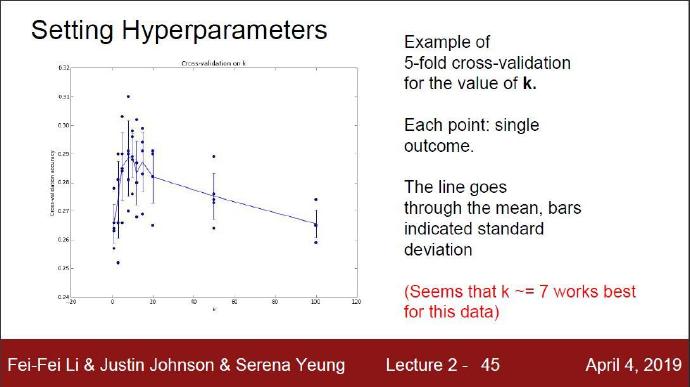
坐标系的横轴是超参数K的取值，纵轴是模型经过交叉验证后在验证集上的精确度。沿着横轴看过去，每个K值我们都进行五次计算（因为是五折运算，可以抽取到5份验证集就能进行五次运算），因此每个K值上方都对应了5个点。接着我们对每个K值的5次计算得到的模型精确度取平均值，并沿横轴依次将不同K值的平均值连接起来的就能得到一条折线段。本例中，当k=7的时算法表现最好（对应图中的准确率峰值）。如果我们将训练集分成更多份数，直线一般会更加平滑（噪音更少）。

在实际情况下，人们不是很喜欢用交叉验证，主要是因为它会耗费较多的计算资源。一般直接把训练集按照50%-90%的比例分成训练集和验证集。但这也是根据具体情况来定的：如果超参数数量多，你可能就想用更大的验证集，而验证集的数量不够，那么最好还是用交叉验证吧。至于分成几份比较好，一般都是分成3、5和10份。 常用的数据分割模式。给出训练集和测试集后，训练集一般会被均分。这里是分成5份。前面4份用来训练，黄色那份用作验证集调优。如果采取交叉验证，那就各份轮流作为验证集。最后模型训练完毕，超参数都定好了，让模型跑一次（而且只跑一次）测试集，以此测试结果评价算法。

2-6 Nearest Neighbor分类器的优劣

现在对Nearest Neighbor分类器的优缺点进行思考。首先，Nearest Neighbor分类器易于理解，实现简单。其次，算法的训练不需要花时间，因为其训练过程只是将训练集数据存储起来。然而测试要花费大量时间计算，因为每个测试图像需要和所有存储的训练图像进行比较，这显然是一个缺点。在实际应用中，我们关注测试效率远远高于训练效率。其实，我们后续要学习的卷积神经网络在这个权衡上走到了另一个极端：虽然训练花费很多时间，但是一旦训练完成，对新的测试数据进行分类非常快。这样的模式就符合实际使用需求。

Nearest Neighbor分类器的计算复杂度研究是一个活跃的研究领域，若干 Approximate Nearest Neighbor (ANN)算法和库的使用可以提升Nearest Neighbor分类器在数据上的计算速度（比如：FLANN）。这些算法可以在准确率和时空复杂度之间进行权衡，并通常依赖一个预处理/索引过程，这个过程中一般包含kd树的创建和k-means算法的运用。

Nearest Neighbor分类器在某些特定情况（比如数据维度较低）下，可能是不错的选择。但是在实际的图像分类工作中，很少使用。因为图像都是高维度数据（他们通常包含很多像素），而高维度向量之间的距离通常是反直觉的。下面的图片展示了基于像素的相似和基于感官的相似是有很大不同的：

四张图片中第一张是原图，另外三张图片是基于原图分别进行了不同方式处理得到的图形。处理1是将部分区域的像素变为0；处理2是将像素水平平移；处理3是对每一个像素进行染色。我们分别计算这三张图与原图的L2距离，发现三者与原图的L2距离都是一样的。也就是说虽然距离一样，但是实际的图片会产生误差。因此用L2距离作为评价指标是存在缺陷的。

维数灾难的概念¹ 下面我们谈谈为什么KNN算法不适合与高维度数据的处理，结合下面这张图就能很好的理解。

随着维度的增加，数据量是呈指数增加的。而KNN要与数据集中的每一个数据进行比对，也就是高维度数据下KNN的效率会大大降低。

2-7 小结

简要说来：

• 介绍了图像分类问题。在该问题中，给出一个由被标注了分类标签的图像组成的集合作为训练集，要求算法能预测没有标签的图像的分类标签，并根据算法预测准确率进行评价。

• 介绍了一个简单的图像分类器：最近邻分类器(Nearest Neighbor classifier)。分类器中存在不同的超参数(比如k值或距离类型的选取)，要想选取好的超参数不是一件轻而易举的事。

• 选取超参数的正确方法是：将原始训练集分为训练集和验证集，我们在验证集上尝试不同的超参数，最后保留表现最好那个。

• 如果训练数据量不够，使用交叉验证方法，它能帮助我们在选取最优超参数的时候减少噪音。

• 一旦找到最优的超参数，就让算法以该参数在测试集跑且只跑一次，并根据测试结果评价算法。

• 最近邻分类器能够在CIFAR-10上得到将近40%的准确率。该算法简单易实现，但需要存储所有训练数据，并且在测试的时候过于耗费计算能力。

• 最后，我们知道了仅仅使用L1距离和L2距离来进行像素比较是不够的，图像更多的是按照背景和颜色被分类，而不是语义主体分身。

在接下来的课程中，我们将专注于解决这些问题和挑战，并最终能够得到超过90%准确率的解决方案。该方案能够在完成学习就丢掉训练集，并在一毫秒之内就完成一张图片的分类。

实际应用 k-NN

如果你希望将k-NN分类器用到实处（最好别用到图像上，若是仅仅作为练手还可以接受），那么可以按照以下流程：

1. 预处理你的数据：对你数据中的特征进行归一化（normalize），让其具有零平均值（zero mean）和单位方差（unit variance）。在后面的小节我们会讨论这些细节。本小节不讨论，是因为图像中的像素都是同质的，不会表现出较大的差异分布，也就不需要标准化处理了。
2. 如果数据是高维数据，考虑使用降维方法，比如PCA或随机投影。
3. 将数据随机分入训练集和验证集。按照一般规律，70%-90% 数据作为训练集。这个比例根据算法中有多少超参数，以及这些超参数对于算法的预期影响来决定。如果需要预测的超参数很多，那么就应该使用更大的验证集来有效地估计它们。如果担心验证集数量不够，那么就尝试交叉验证方法。如果计算资源足够，使用交叉验证总是更加安全的（份数越多，效果越好，也更耗费计算资源）。
4. 在验证集上调优，尝试足够多的k值，尝试L1和L2两种距离计算方式。
5. 如果分类器跑得太慢，尝试使用Approximate Nearest Neighbor库（比如FLANN）来加速这个过程，其代价是降低一些准确率。
6. 对最优的超参数做记录。记录最优参数后，是否应该让使用最优参数的算法在完整的训练集上运行并再次训练呢？因为如果把验证集重新放回到训练集中（自然训练集的数据量就又变大了），有可能最优参数又会有所变化。在实践中，不要这样做。千万不要在最终的分类器中使用验证集数据，这样做会破坏对于最优参数的估计。直接使用测试集来测试用最优参数设置好的最优模型，得到测试集数据的分类准确率，并以此作为你的KNN分类器在该数据上的性能表现。

3 线性分类器

3-1 从图像到标签分值的参数化映射概念的提出

我们将要实现一种更强大的方法来解决图像分类问题，该方法可以自然地延伸到神经网络和卷积神经网络上。这种方法主要有两部分组成：一个是评分函数（score function），它是原始图像数据到类别分值的映射。另一个是损失函数（loss function），它是用来计算预测分类标签与真实标签之间准确度的。该方法可转化为一个最优化问题，在最优化过程中，将通过更新评分函数的参数来最小化损失函数值，以此达到最优的效果。

该方法的第一部分就是定义一个评分函数，这个函数将图像的像素值映射为各个分类的得分，得分高低代表图像属于该类别的可能性高低。下面会利用一个具体例子来展示该方法。

现在假设有一个包含很多图像的训练集$x_i\in R^D$，每个图像都有一个对应的分类标签$y_i$。这里$i=1,2...N$并且$y_i\in 1...K$。这就是说，我们有N个图像样例，每个图像的维度是D，共有K种不同的分类。

举例来说，在CIFAR-10中，我们有一个N=50000的训练集，每个图像有D=32x32x3=3072个像素，而K=10，这是因为图片被分为10个不同的类别（狗，猫，汽车等）。我们现在定义评分函数为：$f:R^D—>R^K$，该函数是原始图像像素到分类分值的映射。

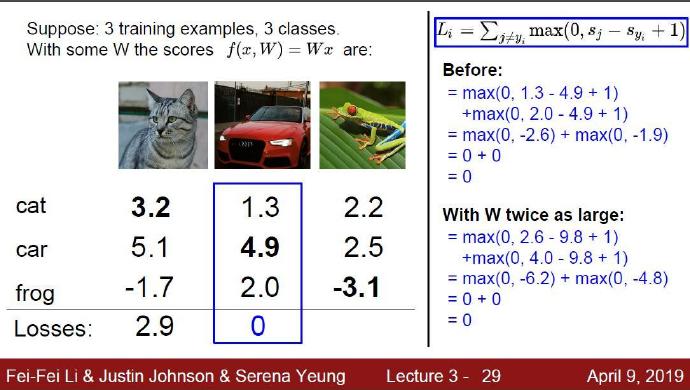
由上图可以看到，通过score function评分函数 我们可以得到每张图片在不同类别中的分数。理想情况下，我们希望图片在正确的标签分类器下的分数是最大的，然而如果没有合理的调优分类器就不能达到这样的效果。

以猫这张图片为例，由于权重W设计的不合理导致猫这张图在猫分类器中的分数为2.9，而在狗分类器中的分数为8.02。这就会导致最后去最高分数为类别的时候，会将这张猫的图片归到狗这个类别中。我们再看下那张红色的车子，这张图片就在车辆这个类别中取得了最高的分数，那么最终分类时就会自然而然的归到车辆这类里。

3-2 理解线性分类器的概念

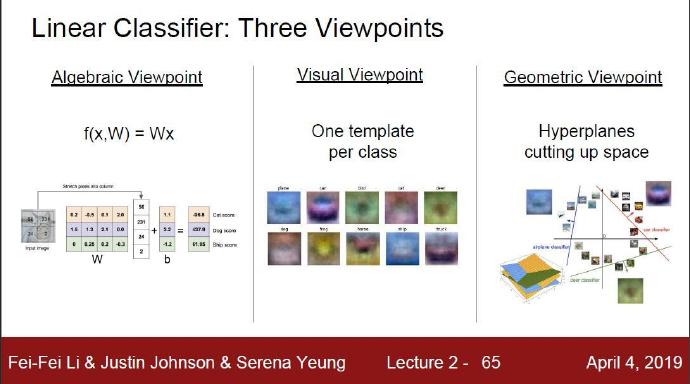
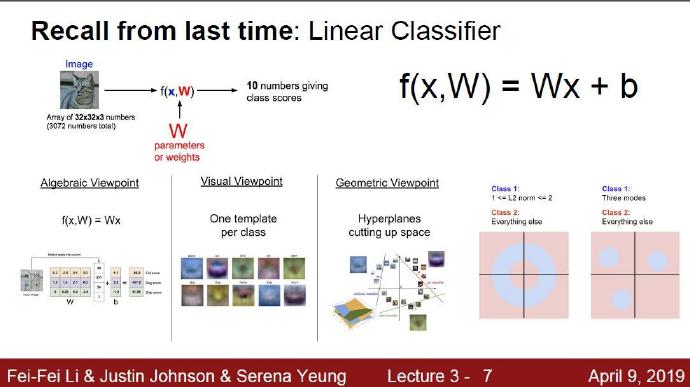
分别从代数角度、可视化角度、几何角度理解线性分类器。

3-2-1 代数角度理解

$f(X_i,W,b)=W{X}_i+b$

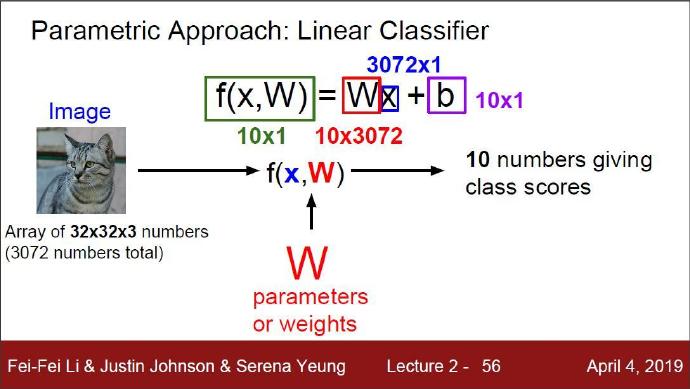
在上面的公式中，假设每个图像数据都被拉长为一个长度为D的列向量，大小为[D x 1]。其中大小为[K x D]的矩阵W和大小为[K x 1]列向量b为该函数的参数（parameters）。还是以CIFAR-10为例，$X_i$就包含了第i个图像的所有像素信息，这些信息被拉成为一个[3072 x 1]的列向量，W大小为[10x3072]，b的大小为[10x1]。因此，3072个数字（原始像素数值）输入函数，函数输出10个数字（不同分类得到的分值）。参数W被称为权重（weights），参数b被称为偏差向量（bias vector），这是因为它影响输出数值，但是并不和原始数据$X_i$产生关联。在实际情况中，人们常常混用权重和参数这两个术语。

上图讲义的讲解：现在我们将32x32x3大小的数据图片转换成长向量，就能得到3072个向量。这3072个向量里的每个向量都是评分函数score function 的自变量，我再给每个自变量赋予特定的权重W 就能得到一条直线。这条直线就是这站图片对应的线性分类器。当然，我们也可以为线性分类器添加偏置量P。

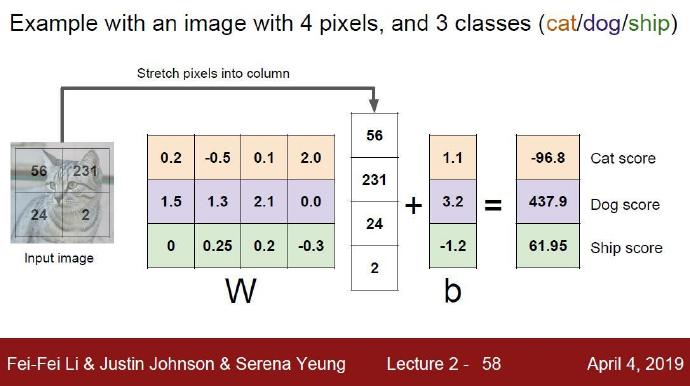
举一个分值分类的例子： 如上图所示，为了便于可视化，假设图像只有4个像素（都是黑白像素，这里不考虑RGB通道），有3个分类（红色代表猫，绿色代表狗，蓝色代表船。W矩阵每一行都是一个类别图像对应的权重值。我们以猫这类图像为例，首先将图像像素拉伸为一个列向量，与W进行矩阵乘，然后得到各个分类的分值。接着我们取出分值最大的那个类别作为测试数据的类别。（注意：这个例子中的权重W设计的一点也不好：猫分类的分值非常低。从上图来看，算法结果倒是觉得这个图像是一只狗。）

需要注意的几点：

• 首先，一个单独的矩阵乘法$W{X}_i$就高效地并行评估10个不同的分类器（每个分类器针对一个分类），其中W的一个行向量就是每个类别的分类器。
• 注意我们认为输入数据$X_i,Y_i$是给定且不可改变的，但参数W和b是可控制改变的。我们的目标就是通过设置这些参数，使得计算出来的分类分值情况和训练集中图像数据的真实类别标签相符。在接下来的课程中，我们将详细介绍如何做到这一点，但是目前只需要直观地让正确分类的分值比错误分类的分值高即可。
• 该方法的一个优势是训练数据是用来学习到参数W和b的，一旦训练完成，训练数据就可以丢弃，留下学习到的参数即可。这是因为一个测试图像可以简单地输入函数，并基于计算出的分类分值来进行分类。
• 最后，注意只需要做一个矩阵乘法和一个矩阵加法就能对一个测试数据分类，这比k-NN中将测试图像和所有训练数据做比较的方法快多了。

3-2-2 可视化角度理解

将线性分类器看做模板匹配：关于权重W的另一个解释是权重W的每一行对应着一个类别的的模板（有时候也叫作_原型_）。一张图像对应不同类别的得分，是通过使用内积（也叫_点积_）来比较图像和模板，然后找到和哪个模板最相似。从这个角度来看，线性分类器就是在利用学习到的模板，针对待分类图像做模板匹配。从另一个角度来看，可以认为还是在高效地使用k-NN，不同的是我们没有使用所有的训练集的图像来比较，而是每个类别只用了一张图片（这张图片是我们学习到的(即权重W的一行），而不是训练集中的某一张），而且我们会使用（负）内积来计算向量间的距离，而不是使用L1或者L2距离。

由上图可以看到，这里展示的是以CIFAR-10为训练集，学习结束后由权重反推得到的每种类型的可视化图片模板。注意，船的模板如期望的那样有很多蓝色像素。如果图像是一艘船行驶在大海上，那么这个模板利用内积计算图像将给出很高的分数。

可以看到马的模板看起来似乎是两个头的马，这是因为训练集中的马的图像中马头朝向各有左右造成的。线性分类器将这两种情况融合到一起了。类似的，汽车的模板看起来也是将几个不同的模型融合到了一个模板中，并以此来分辨不同方向不同颜色的汽车。这个模板上的车是红色的，这是因为CIFAR-10中训练集的车大多是红色的。线性分类器对于不同颜色的车的分类能力是很弱的，但是后面可以看到神经网络是可以完成这一任务的。神经网络可以在它的隐藏层中实现中间神经元来探测不同种类的车（比如绿色车头向左，蓝色车头向前等）。而下一层的神经元通过计算不同的汽车探测器的权重和，将这些合并为一个更精确的汽车分类分值。

3-2-3 几何角度理解

二维数据对应的分类器是二维空间内的直线；三维数据对应的分类器是三维空间里的二维平面；N维数据对应的分类器是N维空间里的N-1维空间。

将图像看做高维度的点：既然图像被伸展成为了一个高维度的列向量，那么我们可以把图像看做这个高维度空间中的一个点（即每张图像是3072维空间中的一个点）。整个数据集就是一个点的集合，每个点都带有1个分类标签。

既然定义每个分类类别的分值是权重和图像的矩阵乘，那么每个分类类别的分数就是这个空间中的一个线性函数的函数值。我们没办法可视化3072维空间中的线性函数，但假设把这些维度挤压到二维，那么就可以看看这些分类器在做什么了：

图像空间的示意图。其中每个图像是一个点，有3个分类器。以红色的汽车分类器为例，红线表示空间中汽车分类分数为0的点的集合，红色的箭头表示分值上升的方向。所有红线右边的点的分数值均为正，且线性升高。红线左边的点分值为负，且线性降低。

3-2-4 线性分类无法处理的问题

由上图可以看到，蓝色和红色分别代表一种类型。图中给出了3种非线性数据，即线性分类器无法对非线性数据进行分类，不能用一条直线对数据进行划分。

• 情形一：异或问题(XOR)
• 情形二：环状数据
• 情形三：多峰值数据

3-3 小结

由上面的线性分类器的例子，我们可以看到参数(权重W和偏置b)对于分类器的分类效果是很大的。那么如何获得效果较好的分类器呢？下一章我们将给出答案，如何优化参数。

4 损失函数和最优化(梯度下降)

4-1 损失函数的初窥

在上一节定义了从图像像素值到所属类别的评分函数（score function），该函数的参数是权重矩阵$W$。在函数中，数据$X_i,Y_i$是给定的，不能修改。但是我们可以调整权重矩阵这个参数，使得评分函数的结果与训练数据集中图像的真实类别一致，即评分函数在正确的分类的位置应当得到最高的评分（score）。

回到之前那张猫的图像分类例子，它有针对"猫"，“狗”，"船"三个类别的分数。我们看到例子中权重值$W$非常差，因为猫分类的得分非常低（-96.8），而狗（437.9）和船（61.95）比较高。我们将使用损失函数（Loss Function）（有时也叫代价函数Cost Function或目标函数Objective）来衡量我们对结果的不满意程度。直观地讲，当评分函数输出结果与真实结果之间差异越大，损失函数输出越大，反之越小。我们的目标就是尽量减小损失函数的输出。

我们对于预测训练集数据分类标签的情况总有一些不满意的，而损失函数就能将这些不满意的程度量化。

4-2 多类支持向量机损失函数 Multiclass SVM Loss

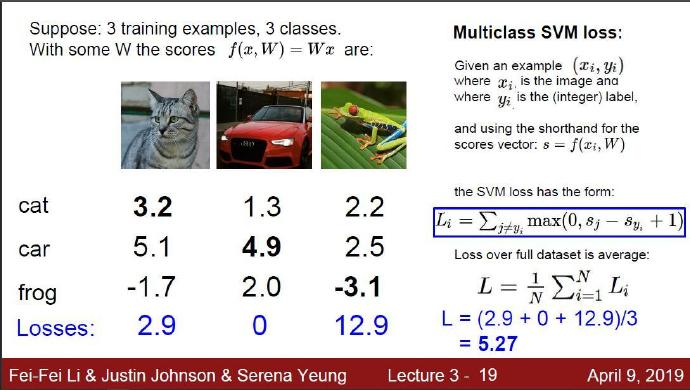
损失函数的具体形式多种多样。首先，介绍常用的多类支持向量机（SVM）损失函数。SVM的损失函数想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值$\Delta$。我们可以把损失函数想象成一个人，这位SVM先生（或者女士）对于结果有自己的品位，如果某个结果能使得损失值更低，那么SVM就更加喜欢它。

让我们更精确一些。回忆一下，第i个数据中包含图像$x_i$的像素和对应的正确类别标签$y_i$。评分函数输入像素数据$x_i$，然后通过公式$f(x_i,W)$来计算不同分类类别的分值。这里我们将分值简写为$s$。比如，针对第j个类别的得分就是分值的第j个元素：$s_j=f(x_i,W{)}_j$。针对第i个数据的多类SVM的损失函数定义如下：

$L_i={\sum }_{j\ne y_i}max(0,s_j-s_{y_i}+\Delta )$

下面对公式进行解释：对每一个分类错误的数据，把他分类错误的分数$s_j$，减去数据正确类别的分数$s_{y_i}$，再加上一个边界值$\Delta$。再用刚刚加减操作得到的数$s_j-s_{y_i}+\Delta$与$0$进行比较取二者中最大的一个。

下面我们以猫为例子计算猫这个数据的损失函数值：

对于参数$\Delta$的理解²：我们可以理解为可允许的损失精度。上面的例子中我们设置的$\Delta =1$，也就是说Loss函数可以容忍与正确分类的分数值$s_{j_i}$的差距小于1的结果存在（也可以理解为Loss函数对于错误小于1的结果是不会计算的）。差距小于设置的$\Delta$的话损失函数值为0，差距大于设置的$\Delta$的话就会计算出具体的损失值。简而言之，SVM的损失函数想要正确分类类$y_i$的分数比不正确类别分数高，而且至少要高$\Delta$。如果不满足这点，就开始计算损失值。（这一段关于$\Delta$的理解可以去cs231n的官方笔记查看）

关于$max(0,-)$函数，它常被称为折页损失（hinge loss）。有时候会听到人们使用平方折叶损失SVM（即L2-SVM），它使用的是$max(0,-{)}^2$，将更强烈（平方地而不是线性地）地惩罚过界的边界值。不使用平方是更标准的版本，但是在某些数据集中，平方折叶损失会工作得更好。可以通过交叉验证来决定到底使用哪个。

将3个种类的损失函数值加起来求平均值，就能得到该模型在这个数据集上的损失函数值。

下面给出几个思考题：

Q1：What happens to loss if car scores change a bit?

A：汽车这类的损失函数值不会变化。假设我们稍微改动一下汽车分类的分数，改为4.7之后得到的损失函数值不变。因为尽管修改了汽车类的分数之后，猫类和青蛙类的分数与汽车类的分数差距仍然大于设置的$\Delta =1$，因此对结果不会产生影响。

Q2：what is the min/max possible loss？

A：根据hinge loss 函数中的max(0,-)，可以知道最小值是0，最大值为无穷大。但取到最小值0的时候，即最理想的结果分类正确。图中的汽车这一类，已经分类正确了。当分类错误的分数为很大很大的时候，loss就会取到无穷大。

Q3：At initialization W is small so all s ≈ 0. What is the loss?（当我们的权重W为初始值随意分布的时候，导致每个分类的评分函数值都十分相近。那么此时的loss损失函数值是多少？）

A：此时的损失函数的值为错误分类的个数。损失函数只计算分类错误的那几项评分函数值，也是就是$S=s_j-s_{y_i}\approx 0$，则经过两次分类错误的计算后得到max(0,0+1)会加2次$1$。

Q4：What if the sum as over all classes?（including $j=y_i$)；（前面我们时当$j\ne y_i$分类不正确时才计算loss，现在我们改变一下规则。当$j=y_i$分类正确时也要计算loss，看看会发生什么？）

A：改变规则后得到的数据比原来的loss的数值上$+1$

Q5：What if we used mean instead of sum?（如果我们不使用求和而使用求平均会发生什么？）

A：我们先来理解下loss函数中的求和，loss函数中用到了2次求和$\sum$。第一次求和是在一个分类中对错误分类的loss值求和得到这个分类的loss值。第二次分类是在整个模型上对不同分类的loss值进行求和得到模型在该数据集上的loss值。Eg：第一次求和是求cat分类中分到dog和frog的loss函数值的总和，得到cat分类的loss函数值。第二次求和是cat分类的loss值和car分类的loss值以及frog分类的loss值求和，得到整个模型在三个数据集上的loss函数值。

接着我们回答下如果改用求平均会发生什么？答案是只对数值产生影响，对于评估模型损失效果并无影响。换句话说就是求平均只是在求和是将所有的loss加起来，而求平均是将所有的loss除以了一个数。除了数值变化外，意义是差不多的。

从Q4和Q5的问题解答中我们可以看出在求loss时不必求正确分类求loss函数值，也不必做平均操作

Q6：What if we used $L_i={\sum }_{j\ne y_i}max(0,s_j-s_{y_i}+\Delta {)}^2$如果我们使用平方折页损失函数会发生什么？）

A：相比于原来的loss函数，添加了平方后会对数值产生放大效应。但是loss函数的大小顺序顺序是不会改变的，对于细微的差距能被平方扩大，便于观察。

代码实现 Multiclass SVM Loss ：

def L_i_vectorized(x,y,W):
    scores=W.dot(x)
    margins=np.maximum(0,scores-scores[y]+1)
    margins[y]=0
    loss_i=np.sum(margins)
    return loss_i

cifar-10 数据集中有50000张十种分类的图片，每个分类的scores函数是10x1的矩阵。于是我们就能得到50000行x10列的scores矩阵。³

那么在这次的模型中，我们面对的是线性评分函数$f(x_i,W)=W{x}_i$，所以我们可以将损失函数的公式稍微改写一下：

$L_i={\sum }_{j\ne y_i}max(0,w_j^T{x}_i-w_{y_i}^T{x}_i+\Delta )$

其中$w_j$是权重$W$的第$j$行，被变形为列向量。然而，一旦开始考虑更复杂的评分函数$f$公式，这样不必将线性评分函数的细节放到公式中。

猜想一下：如果我们找到了一个合适的权重W，使得在这个权重下损失函数值loss为0。那么这十分有效的权重W是独一无二的吗？

答案：权重W不是唯一的。我们将W乘以2，用2W去做线性分类也能得到loss=0的结果。从这里我们可以看出权重不是唯一，而是各行之间的比例大小关系。下面的例子就是比较权重W和权重2W的loos结果：

那么问题又来了！既然权重W和2W的结果是一样的，哪我们该选W还是2W作为权重呢？

根据奥卡姆剃刀原理：如无必要，勿增实体。我们选择简单小巧的W作为权重。

4-3 正则化 Regularization

上面损失函数有一个问题。假设有一个数据集和一个权重集W能够正确地分类每个数据（即所有的边界都满足，对于所有的i都有$L_i=0$。问题在于这个W并不唯一：可能有很多相似的W都能正确地分类所有的数据。一个简单的例子：如果W能够正确分类所有数据，即对于每个数据，损失值都是0。那么当$\lambda >1$时，任何数乘$\lambda W$都能使得损失值为0，因为这个变化将所有分值的大小都均等地扩大了，所以它们之间的绝对差值也扩大了。举个例子，如果一个正确分类的分值和举例它最近的错误分类的分值的差距是15，对W乘以2将使得差距变成30。

换句话说，我们希望能向某些特定的权重W添加一些偏好，对其他权重则不添加，以此来消除模糊性。这一点是能够实现的，方法是向损失函数增加一个正则化惩罚（regularization penalty）$R(W)$部分。最常用的正则化惩罚是L2范式，L2范式通过对所有参数进行逐元素的平方惩罚来抑制大数值的权重：

$R(W)={\sum }_k{\sum }_l{W}_{k,l}^2$

上面的表达式中，将$W$中所有元素平方后求和。注意正则化函数不是数据的函数，仅基于权重。包含正则化惩罚后，就能够给出完整的多类SVM损失函数了，它由两个部分组成：数据损失（data loss），即所有样例的的平均损失$L_i$；以及正则化损失（regularization loss）。

即在原有的损失函数的基础上，添加一个正则化的项$R(w)$。而正则化的强度用参数$\lambda >1$来控制。完整公式如下所示：

$$L=\underset{dataloss}{\frac{1}{N}\sum _i{L}_i}+\underset{regularizationloss}{\lambda R(W)}$$

正则化：目的就是防止过拟合现象

关于$R(w)$的设定：可以使用L2正则化，也可以用L1正则化。也可以使用既含有L1又含有L2的弹性网络Elastic net (L1 + L2)。

还有一些更为复杂的正则化操作：Dropout、Batch normalization、Stochastic depth、 fractional pooling等。

为什么要正则化？正则化能够更好的表达权重W，通过正则化还能够让模型更简单，防止过拟合现象的产生。

下面通过一个例子看看正则化为什么能得到权重更好：

我们假设输入x都是一样的，现在定义两个不同模型。第一个模型的权重是$W_1$，第二个模型的权重是$W_2$。这两个模型的进行线性求和后得到的结果都是1，那么用那个模型的权重比较好呢？答案是第二个模型比较好。我们用L2正则化来理解，第一个模型正则化L2的值为1，第二个模型正则化的值为$(0.25{)}^2\ast 4$。可以看出第二个模型的正则化项比较小，能避免权重过于突出将权重均匀分配，导致过拟合。

4-4 Softmax()分类器

SVM是最常用的两个分类器之一，而另一个就是**Softmax分类器，**它的损失函数与SVM的损失函数不同。对于学习过二元逻辑回归分类器的读者来说，Softmax分类器就可以理解为逻辑回归分类器面对多个分类的一般化归纳。SVM将输出$f(x_i,W)$作为每个分类的评分（因为无定标，所以难以直接解释）。与SVM不同，Softmax的输出（归一化的分类概率）更加直观，并且从概率上可以解释，这一点后文会讨论。

在Softmax分类器中，函数映射$f(x_i,W)=W{x}_i$保持不变，但将这些评分值视为每个分类的未归一化的对数概率，并且将损失函数从_折叶损失函数（hinge loss）_替换为交叉熵损失函数（cross-entropy loss）。损失函数公式如下：

$Li=-log(\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}})$ 或等价的$L_i=-f_{y_i}+\log ({\sum }_j{e}^{f_j})$

在上式中，使用$f_j$来表示分类评分向量$f$中的第j个元素，$f_{y_j}$表示正确分类的评分。和之前一样，整个数据集的损失值是数据集中所有样本数据的损失值$L_i$的均值与正则化损失$R(W)$之和。其中函数

$$f_j(z)=\frac{e^{z_j}}{{\sum }_k{e}^{z_k}}$$

被称作softmax 函数：其输入值是一个向量，向量中元素为任意实数的评分值（$z$中的），函数对其进行压缩，输出一个向量，其中每个元素值在0到1之间，且所有向量元素之和为1。所以，包含softmax函数的完整交叉熵损失看起唬人，实际上还是比较容易理解的。

先用score function评分函数计算，之后将每个分类的得分$s_j$进行指数运算$e^{s_j}$；然后进行归一化过程。因为exp函数是一个恒大于零的函数，这样就能很好的解决评分出现负值现象。另外exp函数是单调函数，能够保证不同分类之间的分数大小排序保持原样不变。最后求和归一化，得到概率。

损失函数的定义：损失函数的自变量是每个分类的概率。因为 $-\log (x)$函数在x=1时取得0，即正确分类的概率为1时损失为0；如果正确分类概率越低，损失函数$-\log (x)$的值越趋近于无穷大。

这里可以去看下 ML机器学习cs229中的极大似然估计

这里要着重理解信息论中的熵，交叉熵

信息理论视角：在"真实"分布$p$和估计分布$q$之间的_交叉熵_定义如下：

$H(p,)=-{\sum }_{x}p(x){\log }_{q(x)}$

因此，Softmax分类器所做的就是最小化在估计分类概率（就是上面的$e^{f_{y_i}}/{\sum }_j{e}^{f_j}$）和"真实"分布之间的交叉熵，在这个解释中，"真实"分布就是所有概率密度都分布在正确的类别上（比如：$p=[0,...1,...,0]$）中在$y_i$的位置就有一个单独的1）。还有，既然交叉熵可以写成熵和相对熵（Kullback-Leibler divergence）![H(p,q)=H(p)+D_{KL}(p||q)][26]，并且delta函数![p][20]的熵是0，那么就能等价的看做是对两个分布之间的相对熵做最小化操作。换句话说，交叉熵损失函数"想要"预测分布的所有_概率密度_都在正确分类上。

译者注：Kullback-Leibler差异（Kullback-Leibler Divergence）也叫做相对熵（Relative Entropy），它衡量的是相同事件空间里的两个概率分布的差异情况。

概率论解释：先看下面的公式：

$P(y_i|x_i,W)=\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}}$

可以解释为是给定图像数据$x_i$，以$W$为参数，分配给正确分类标签$y_i$的归一化概率。为了理解这点，请回忆一下Softmax分类器将输出向量$f$中的评分值解释为没有归一化的_对数概率_。那么以这些数值做指数函数的幂就得到了没有归一化的概率，而除法操作则对数据进行了归一化处理，使得这些概率的和为1。从概率论的角度来理解，我们就是在最小化正确分类的负对数概率，这可以看做是在进行_最大似然估计_（MLE）。该解释的另一个好处是，损失函数中的正则化部分$R(W)$可以被看做是权重矩阵$W$的高斯先验，这里进行的是最大后验估计（MAP）而不是最大似然估计。提及这些解释只是为了让读者形成直观的印象，具体细节就超过本课程范围了。

**实操事项：数值稳定。**编程实现softmax函数计算的时候，中间项$e^{f_{y_i}}$和$su{m}_j{e}^{f_j}$因为存在指数函数，所以数值可能非常大。除以大数值可能导致数值计算的不稳定，所以学会使用归一化技巧非常重要。如果在分式的分子和分母都乘以一个常数$C$并把它变换到求和之中，就能得到一个从数学上等价的公式：

$\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}}=\frac{C{e}^{f_{y_i}}}{C{\sum }_j{e}^{f_j}}=\frac{e^{f_{y_i}+logC}}{{\sum }_j{e}^{f_j+logC}}$

$C$的值可自由选择，不会影响计算结果，通过使用这个技巧可以提高计算中的数值稳定性。通常将$C$设为$logC=-ma{x}_j{f}_j$。该技巧简单地说，就是应该将向量$f$中的数值进行平移，使得最大值为0。代码实现如下：

    f = np.array([123, 456, 789]) # 例子中有3个分类，每个评分的数值都很大
    p = np.exp(f) / np.sum(np.exp(f)) # 不妙：数值问题，可能导致数值爆炸
    
    # 那么将f中的值平移到最大值为0：
    f -= np.max(f) # f becomes [-666, -333, 0]
    p = np.exp(f) / np.sum(np.exp(f)) # 现在OK了，将给出正确结果

让人迷惑的命名规则：精确地说，SVM分类器使用的是_折叶损失（hinge loss），有时候又被称为_最大边界损失（max-margin loss）。Softmax分类器使用的是_交叉熵损失（corss-entropy loss）_。Softmax分类器的命名是从_softmax函数_那里得来的，softmax函数将原始分类评分变成正的归一化数值，所有数值和为1，这样处理后交叉熵损失才能应用。注意从技术上说"softmax损失（softmax loss）"是没有意义的，因为softmax只是一个压缩数值的函数。但是在这个说法常常被用来做简称。

4-5 SVM和Softmax的比较

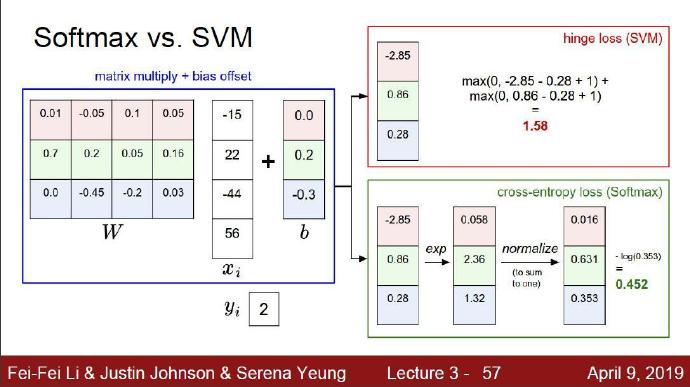
针对一个数据点，SVM和Softmax分类器的不同处理方式的例子。两个分类器都通过线性分类器计算了同样的分值向量f（本节中是通过矩阵乘来实现）。不同之处在于对f中分值的解释：SVM分类器将它们看做是分类评分，它的损失函数鼓励正确的分类（本例中是蓝色的类别2）的分值比其他分类的分值高出至少一个边界值。Softmax分类器将这些数值看做是每个分类没有归一化的对数_概率_，鼓励正确分类的归一化的对数概率变高，其余的变低。SVM的最终的损失值是1.58，Softmax的最终的损失值是0.452，但要注意这两个数值没有可比性（因为使用的不是同一个损失计算方法）。只在给定同样数据，在同样的分类器的损失值计算中，比较损失值才有意义。

4-6小结

我们得到数据集后，通过线性分类 评分函数得到数据在各个分类上的评分。接着我们可以依据这些分数选择不同的损失函数计算。我们可以选择Softmax的交叉熵损失函数，也可以选择SVM的hinge loss折页损失函数。最后我们加上一个正则化项$R(W)$就得到了模型的损失。

5 最优化 Optimization

在上一节中，我们介绍了图像分类任务中的两个关键部分：

1. 基于参数的**评分函数。**该函数将原始图像像素映射为分类评分值（例如：一个线性函数）。

2. 损失函数。该函数能够根据分类评分和训练集图像数据实际分类的一致性，衡量某个具体参数集的质量好坏。损失函数有多种版本和不同的实现方式（例如：Softmax或SVM）。

对于图像数据$x_i$，如果基于参数集$W$做出的分类预测与真实情况比较一致，那么计算出来的损失值$L$就很低。现在介绍图像分类任务中第三个关键部分，也是最后一个关键部分：最优化Optimization。最优化是寻找能使得损失函数值最小化的参数$W$的过程。

铺垫：一旦理解了这三个部分是如何相互运作的，我们将会回到第一个部分（基于参数的函数映射），然后将其拓展为一个远比线性函数复杂的函数：首先是神经网络，然后是卷积神经网络。而损失函数和最优化过程这两个部分将会保持相对稳定。

5-1最优化的策略

Assignment_1

在开始写assignment1前，我们需要下载cifar10数据集。在cs231n的项目中，已经给出了获取的cifar10数据集的get_datasets.sh脚本命令。如果使用的是linux os 则直接在对应目录下运行sh命令即可。如果用的是Windows os 则要下载git来运行sh获取cifar10数据集。或者去cifar10数据集官网下载数据集，如何导入到本地。

官网下载数据集并从本地导入数据到项目中

The cifar-10 datasets 访问官网下载对应python版本的数据集 CIFAR-10 python version，接着将得到的压缩包放到cs231n的datasets文件夹下。最后再用git运行以下get_datasets.sh命令，就会得到数据集。或者解压出来得到的data_batch数据，放到项目的datasets目录下。

在pycharm的终端中输入 jupyter notebook打开jupyter notebook，接着找到knn.ipynb文件点开就会看到assignment1的具体内容。

Q1-1 K-Nearest Neighbor （KNN）exercise K-近邻算法

环境： python（anaconda）

作业内容：

• 训练。
  读取训练数据并存储。

• 测试。
  对于每一张测试图像，KNN把它与训练集中的每一张图像计算距离，找出距离最近的ｋ张图像．这ｋ张图像里，占多数的标签类别，就是测试图像的类别。
  计算图像的距离有两种方式，分别是L1距离和L2距离．具体使用哪种距离度量呢？这就需要我们进一步探索啦！

• k的取值通过交叉验证得到。
  对于KNN算法，k值的选择十分重要。较小的k值容易受到噪声的干扰，较大的k值会导致边界上样本的分类有歧义．
  Note： k值，为了得到较为合适的ｋ值，我们使用交叉验证的方法。

---

1. 什么是维数灾难？ in chapter 2-6 ↩︎

2. 在hinge loss 中关于 $\Delta$的理解 那段注释的内容存疑。in chapter 4-2 ↩︎

3. 这段代码的 W.dot(x)得到的矩阵维度 需要理解下。 in chapter 4-2 ↩︎