强化学习百度训练营学习笔记总结
百度强化学习训练营学习总结
- 强化学习入门
- 定义及其思想
- 组成
- 应用场景
- 与人工智能与其他机器学习的关系
- 强化学习方案分类
- 基于价值学习 Value-based
- 表格方法学习
- MDP和四元组
- Q表格
- 时序差分更新 Temporal Difference 单步更新
- E-greedy
- Sarsa
- Q-learning
- On-policy vs Off=policy
- DQN
- 经验回放
- 固定Q目标
- DQN流程
- 基于策略学习 Policy-based
- 优化策略
- 蒙特卡洛与时序差分更新
- Policy Gradient流程
- 连续动作空间上求解RL——DDPG
- DDPG与DQN对比
- DDPG流程
- 编程实践
- 平台使用
- 与环境交互
- 开源库算法支持对比
- 后记
- 参考
强化学习入门
定义及其思想
强化学习(英语:Reinforcement learning,简称RL)是机器学习中的一个领域,强调如何基于环境而行动,以取得最大化的预期利益。
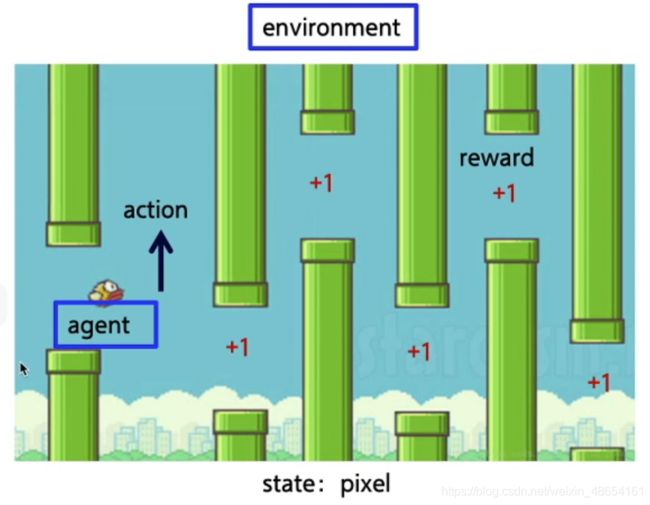
核心思想:智能体agent在环境environment中学习,根据环境的状态state(或观测到的observation),执行动作action,并根据环境的反馈 reward(奖励)来指导更好的动作。
下面举一下现实例子:
如图所示,强化学习基础步骤可以流程化为:
组成
应用场景
游戏(马里奥、Atari、Alpha Go、星际争霸等)
例子:Flappy bird
机器人控制(机械臂、机器人、自动驾驶、四轴飞行器等)
用户交互(推荐、广告、NLP等)
例子:个性化推荐系统
environment:资源列表,手机用户
agent:app客户端
action:生成推荐选项
state:
reward:用户点击与否
交通(拥堵管理等)
资源调度(物流、带宽、功率等)
金融(投资组合、股票买卖等)
其他
与人工智能与其他机器学习的关系

与其他机器学习对比:
监督学习:侧重于从标注的信息中获取知识 任务驱动-认知
非监督学习:从无标注信息中自己总结规律 数据驱动-认知
强化学习:通过试错获得人生的经验 环境驱动-决策
强化学习方案分类

Value-based: 每个状态被赋予价值(V)并在学习中被优化,最后成为确定性的策略
Policy-based:策略概率函数化,优化后仍然有随机性
基于价值学习 Value-based
表格方法学习
MDP和四元组

个人理解:Q代表后天个体对任务以及环境的理解的量化收益,可以因为学习而改变。而R则是环境或任务先天决定的最终步骤完成收益,不能改变。
Q表格
可以理解为个体对环境的理解,即某种动作作用后会对本身产生正面或者负面的影响,由此可得出下一部动作的偏好。在熊的例子中如图:

那么如何求得Q表格的值呢?结合实际,人类判断当前应该做出哪种决定时往往考虑行为后的收益,而每一个小收益又会受最终目标完成时收益的影响。由此我们先定义一下远期收益G;

其中γ为衰减因子,通常取0~1之前,越大则表明未来收益对当前影响越大。下面是乌龟找路的例子:

表格中Q为当前动作后的全局收益G。知道了全局收益之后我们就可以用全局收益去更新当前步的收益,这个过程称之为状态价值迭代。可以参考Stanford大学的小应用。
可以看到初始设置下只有少数格子具有收益R,默认算法设定下,小球会自动探索从初始点到高收益点的路径。 在不断学习过程中,小球会逐渐对每个小格子的收益Q做出改变,形成一条确定性的道路,从而使自己更容易获得最终的收益。
时序差分更新 Temporal Difference 单步更新
E-greedy
Sarsa
Sarsa全称是state-action-reward-state’-action’,目的是学习特定的state下,特定action的价值Q,最终建立和优化一个Q表格,以state为行,action为列,根据与环境交互得到的reward来更新Q表格,更新公式为:

Sarsa在训练中为了更好的探索环境,采用ε-greedy方式来训练,有一定概率随机选择动作输出。

Q-learning
Q-learning也是采用Q表格的方式存储Q值(状态动作价值),决策部分与Sarsa是一样的,采用ε-greedy方式增加探索。
Q-learning跟Sarsa不一样的地方是更新Q表格的方式。
Sarsa是on-policy的更新方式,先做出动作再更新。
Q-learning是off-policy的更新方式,更新learn()时无需获取下一步实际做出的动作next_action,并假设下一步动作是取最大Q值的动作。
Q-learning的更新公式为:

与Sarsa的区别:目标策略与探索策略分离,下一步动作选择导致的收益并不影响这一步Q的学习;即不会像Sarsa一样考虑下一步动作可能导致的危险而最终学习一条较为保守的安全路线,Q-learning的学习结果相对激进。
On-policy vs Off=policy
DQN
使用Q表格学习有一个致命缺点就是状态有限且在表格极大时内存占用很大,实际生活中有许多问题都是有近乎无穷状态的,比如象棋围棋等。所以我们在将强化学习应用在这些场景时往往使用函数近似的方法。
值函数近似的方法又主要分为多项式函数和神经网络法,本文中主要介绍神经网络方法。
相比于Q表格面神经网络的另一个优点就是能泛化未知的输入状态,像已知状态靠近并且输出值;而Q表格则不能处理未知状态。
以下为用神经网络拟合Q表格与不同监督学习过程异同对比。

经验回放
DQN利用Qlearning特点,目标策略与动作策略分离,学习时利用经验池储存的经验取batch更新Q。同时提高了样本的利用率,也打乱了样本状态相关性使其符合神经网络的使用特点。
固定Q目标
神经网络一般学习的是固定的目标,而Qlearning中Q同样为学习的变化量,变动太大不利于学习。所以DQN使Q在一段时间内保持不变,使神经网络更易于学习。
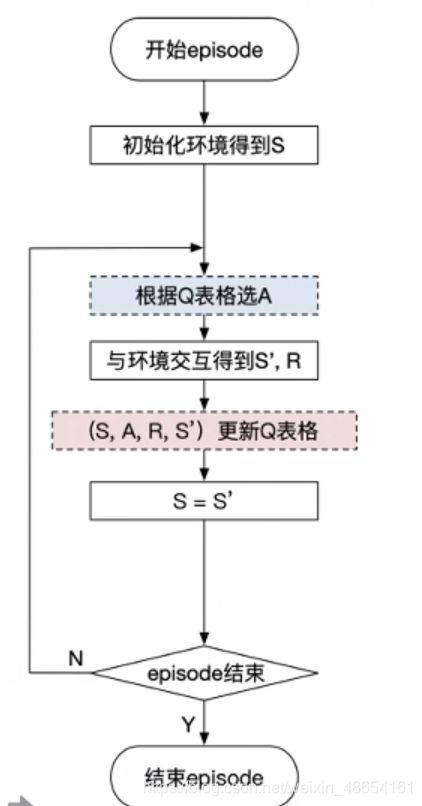
DQN流程
基于策略学习 Policy-based
Policy-based 本身属于一种随机性策略,这点与DQN不同。DQN策略确定后就会输出相同的动作,而随机性策略即使网络优化完成仍然是输出动作概率。(对石头剪子布游戏有奇效)

每一轮行动与环境交互序列直到结果出现为止称作一个Episode(比如说一轮乒乓球21分结束有胜负),优化目标就是是每个Episode的Reward总和最大。而这一个episode所有行动与环境交互序列称为Trajectory。其发生概率以及期望回报可以表示以及近似为:

总回报R定义为每个步骤reward之和;当样本数量N足够大时我们可以把期望回报公式近似如上。
优化策略
由于优化目标为期望回报,所以我们就是希望他越大越好。故不同于DQN,此处我们采用梯度上升策略。

其中θ为指定状态下动作选择的概率分布,也是本优化问题的变量。
蒙特卡洛与时序差分更新
以下介绍两种更新方式,本文主要是用MC蒙特卡洛方法。

下图给出每一步未来总收益G关于reward的计算方法:

伪代码如下:

用Cross Entropy更新概率分布θ:
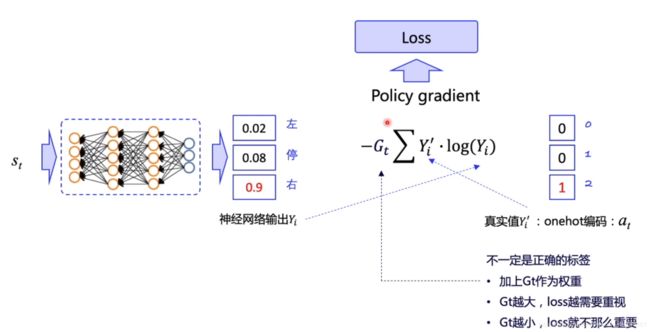
由于目标动作也非实际正确动作,所以加上Gt作为权重修正学习方向。所有trajectory(S,a,G)已知,分别求出每一步Loss并且求和,即可放入优化器求解。
Policy Gradient流程
连续动作空间上求解RL——DDPG
以上介绍的几种方法都是离散空间可以使用的策略,但如果涉及连续空间领域如机器人手臂转角、自动驾驶汽车方向盘转角等以上几种方法就不能使用了。根据这种特点我们将Policy网络输出变为浮点数而非确定动作的概率。

DDPG与DQN对比
与DQN相比,在DDPG中动作是状态的函数,而非根据Q来直接选择。

与DQN相同的,同时具有策略网络和目标网络从而保证计算稳定性。
个人理解:由于策略网络要根据Q网络的评价来学习,所以Q网络必须比策略网络有更大的学习率,才能保证策略网络学习的方向正确已经系统更快稳定。
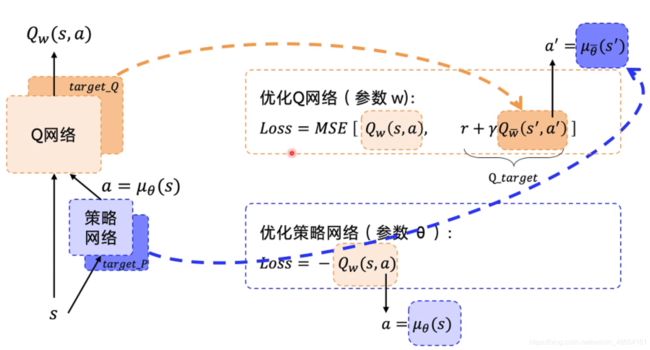
DDPG流程
编程实践
关于编程的细节新手水平有限也在这里就不再赘述了,可以参看百度Parl库demo。细节代码讲解部分也可以参考百度课程。
平台使用
与环境交互
开源库算法支持对比
后记
啊啊啊 萌新的第一篇CSDN学习笔记,主要还是为了方便自己以后复习与对课程及记录,同时也希望能够帮助到其他和我一样非科班出身的同学更方便地理解强化学习,所以着重在课程相关概念梳理部分,忽略了关于代码的描述和总结。也还是因为我代码方面的底子弱,实在无法做出有价值的经验分享,不过争取在以后的磨炼里在代码方面有所进步啦!如果发现本文有纰漏的地方还请各位大佬不吝赐教~
参考
[1] https://aistudio.baidu.com/aistudio/education/group/info/1335
[2] https://github.com/PaddlePaddle/PARL/tree/develop/examples/tutorials















