算法思考-最大子序列和

题目：对给定的某序列，给出方案求 子序列和 最大的子序列并进行评价

---

一共有四种方法：

1. 求出以每一个元素为起点的每一个子序列的和，再进行比较，找出其中的最大值；

2. 求出以每一个元素为起点的最大子序列的和，再进行比较，找出其中的最大值；

3. 采用分治法，利用递归进行求解；

4. 利用动态规划，遍历序列，实时更新最大子序列和。

   方法一时间复杂度为O(N³)，方法二时间复杂度为O(N²)，方法三时间复杂度为O(N·logN)，方法四时间复杂度为O(N)。

方法一和方法二只是用多个for循环嵌套，比较简单就不写出来了，这里主要讲方法三和方法四。

递归求解

       主要思路为将序列从中间分开，分别求：

以分割点为起点向左的最大连续序列和
以分割点为起点享有的最大连续序列和
横跨分割点的最大连续序列和

       递归计算直到序列长度为1，此时若这个数不是负数，最大子序列和就是其本身，否则为0。

Python代码：

def recursion(l, left, right):
    if left == right:   # 当序列长度为1时
        return max(l[left], 0)

    center = int((left+right)/2)    # 分割点

    maxLeft = recursion(l, left, center)    # 计算左半部分最大子序列和
    maxRight = recursion(l, center+1, right)    # 计算右半部分最大子序列和

    # 计算横跨分割点的最大子序列和
    maxCross = l[center]
    leftIndex = center-1
    rightIndex = center+1
    while leftIndex >= left and l[leftIndex] >= 0:
        maxCross += l[leftIndex]
        leftIndex -= 1
    while rightIndex <= right and l[rightIndex] >= 0:
        maxCross += l[rightIndex]
        rightIndex += 1

    # 返回三者中的最大值
    maxSum = max(maxLeft, maxCross, maxRight)
    return maxSum

C++代码：

#include 

int max(int a, int b, int c){
	if (a > b){
		if (a > c) return a;
		else return c;
	}
	else{
		if (c < b) return b;
		else return c;
	}
}

int recursion(int l[], int left, int right){
	if (left == right) return l[left]>0 ? l[left] : 0;
	
	int center = (left + right) / 2;
	int maxLeft = recursion(l, left, center);
	int maxRight = recursion(l, center+1, right);

    int maxCross = l[center];
    int leftIndex = center-1;
    int rightIndex = center+1;
    while (leftIndex >= left && l[leftIndex] >= 0){
        maxCross += l[leftIndex];
        leftIndex -= 1;
	}
    while (rightIndex <= right && l[rightIndex] >= 0){
        maxCross += l[rightIndex];
        rightIndex += 1;
	}
    int maxSum = max(maxLeft, maxCross, maxRight);
    
    return maxSum;
}

int main(){
	int l[] = {85, -57, -43, 95, -74, -81, -15, 83, 31, 74};
	printf("%d", recursion(l, 0, 9));
}

动态规划求解

       主要思路为：初始最大子序列和为0，从头开始遍历序列，若当前元素不是负数，则累加当前元素，否则将之前的累加结果与最大子序列和比较，选出较大值作为新的最大子序列和，清空当前累加结果。直到遍历序列结束。

Python代码：

def dynamicPlanning(l):
    tmp = 0
    max = 0
    i = 0
    while i < len(l):
        tmp += l[i]
        if tmp > max:
            max = tmp
        if tmp < 0:
            tmp = 0
        i += 1
    return max

C++代码：

#include 

int dynamicPlanning(int l[]){
	int tmp = 0;
	int max = 0;
    for(int i = 0; i<10; i++){
    	tmp += l[i];
        if (tmp > max) max = tmp;
        if (tmp < 0) tmp = 0;
	}
        
    return max;
}

int main(){
	int l[] = {85, -57, -43, 95, -74, -81, -15, 83, 31, 74};
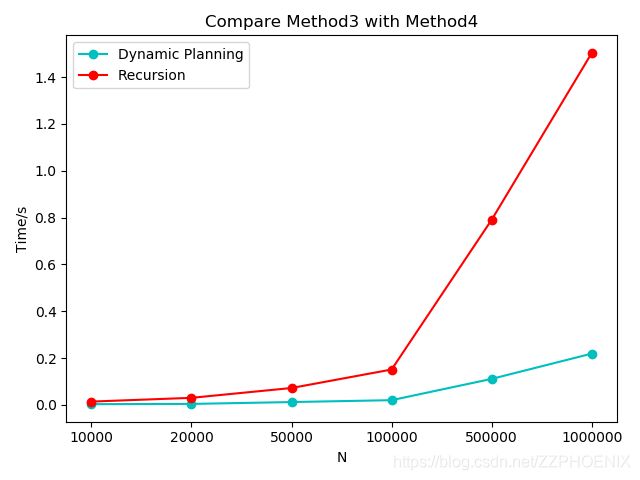
	printf("%d", dynamicPlanning(l));
}

两种方法直观比较：

纵坐标为耗时，横坐标为序列长度，序列内元素取值范围为[-100, 100]，类型为整数