机器人学——3.2-正运动学
机械臂的正运动学通常表述为如下的函数形式:
ξ E = K ( q ) \xi_E=\mathcal{K}(q) ξE=K(q)它表明末端执行器的位姿是基于关节坐标的一个函数。若使用齐次变换,其表达式将是由之前推导的连杆坐标系变换矩阵方程所给的单个连杆变换矩阵 j − 1 A j ^{j-1}A_j j−1Aj 的简单乘积。对于一个 N N N 轴机械臂,有
ξ E ∼ 0 T E = 0 A 1 1 A 2 ⋯ N − 1 A N \xi_E\sim{}^0T_E={}^0A_1{}^1A_2\cdots{}^{N-1}A_N ξE∼0TE=0A11A2⋯N−1AN
对于任何一个串联机械臂,无论其关节的数量和类型如何,都可以计算出其正向运动学的解。我们以后会详细讨论如何确定机器人上每个连杆的 D-H 参数。
末端执行器的位姿 ξ E ∼ T E ∈ S E ( 3 ) \xi_E\sim T_E\in SE(3) ξE∼TE∈SE(3) 共有 6 6 6 个自由度—— 3 3 3 个移动自由度和 3 3 3 个转动自由度。因此为了使末端执行器具有任意的位姿,机械臂通常具有 6 6 6 个关节或者自由度。对于一个 6 6 6 轴机器人,其总的变换矩阵通常被写作 T 6 T_6 T6。
两连杆机器人
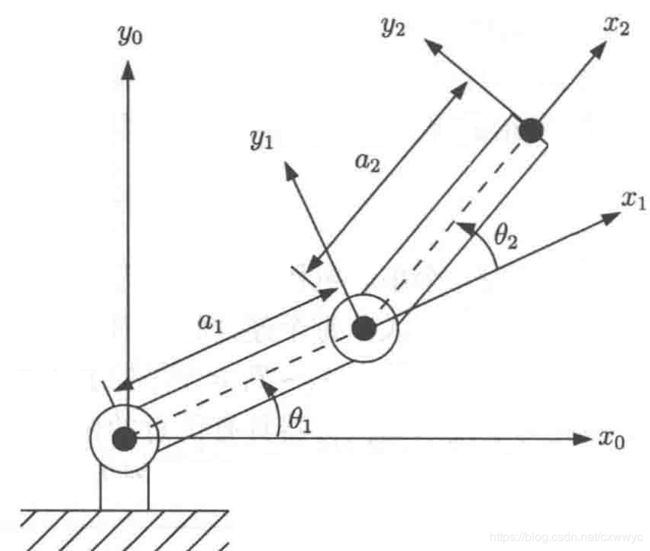
我们讨论一个如图所示的两连杆平面机械手。它的 D-H 参数如下
| 连杆 | θ i \theta_i θi | d i d_i di | a i a_i ai | α i \alpha_i αi | σ i \sigma_i σi |
|---|---|---|---|---|---|
| 1 1 1 | q 1 q_1 q1 | 0 0 0 | 1 1 1 | 0 0 0 | 0 0 0 |
| 2 2 2 | q 2 q_2 q2 | 0 0 0 | 1 1 1 | 0 0 0 | 0 0 0 |
然后我们用这些参数创建一个Link对象的向量:
>> L(1) = Link([0 0 1 0]);
>> L(2) = Link([0 0 1 0]);
>> L
L =
theta=q1, d= 0, a= 1, alpha= 0, offset= 0 (R,stdDH)
theta=q2, d= 0, a= 1, alpha= 0, offset= 0 (R,stdDH)
这个向量将被传递给构造函数SerialLink:
>> two_link = SerialLink(L, 'name', 'two link');
>> two_link
two_link =
two link (2 axis, RR, stdDH, fastRNE)
+---+-----------+-----------+-----------+-----------+-----------+
| j | theta | d | a | alpha | offset |
+---+-----------+-----------+-----------+-----------+-----------+
| 1| q1| 0| 1| 0| 0|
| 2| q2| 0| 1| 0| 0|
+---+-----------+-----------+-----------+-----------+-----------+
grav = 0 base = 1 0 0 0 tool = 1 0 0 0
0 0 1 0 0 0 1 0 0
9.81 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1
它将会返回一个SerialLink对象,显示如下:它为这个机器人提供了一种简明的描述。可以看出,该机器人的结构字符串为“RR”,表明它有两个转动关节,而且它是使用标准的 D-H 参数定义的,另外重力默认作用于z轴方向(与机器人运动平面垂直)。同时对象中还列出了连杆的运动学参数,而关节变量用“q1”和“q2”表示。我们还为机器人取了一个名字,它在任何时候显示机器人时都会出现。输入指令:
>> mdl_planar2
它将直接执行上述步骤,将该机器人定义在 MATLAB 的工作空间,并创建名为twolink的SerialLink对象。
SerialLink对象的一些简单的操作如下
>> two_link.n
ans =
2
该指令返回关节数目。
>> links = two_link.links
links =
theta=q1, d= 0, a= 1, alpha= 0, offset= 0 (R,stdDH)
theta=q2, d= 0, a= 1, alpha= 0, offset= 0 (R,stdDH)
该指令返回一个Link对象的向量,Link对象中包含机器人。我们还可以复制一个SerialLink对象,并命名为foo:
>> clone = SerialLink(two_link, 'name', 'foo')
clone =
foo (2 axis, RR, stdDH, fastRNE)
+---+-----------+-----------+-----------+-----------+-----------+
| j | theta | d | a | alpha | offset |
+---+-----------+-----------+-----------+-----------+-----------+
| 1| q1| 0| 1| 0| 0|
| 2| q2| 0| 1| 0| 0|
+---+-----------+-----------+-----------+-----------+-----------+
grav = 0 base = 1 0 0 0 tool = 1 0 0 0
0 0 1 0 0 0 1 0 0
9.81 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1
现在可以让机械臂工作了。正向运动学的计算使用了fkine方法。这个例子中, q 1 = q 2 = 0 q_1=q_2=0 q1=q2=0。
>> two_link.fkine([0 0])
ans =
1 0 0 2
0 1 0 0
0 0 1 0
0 0 0 1
该方法将返回代表机器人第二个连杆坐标系位姿的齐次变换 T 2 T_2 T2。对于一个不同的位形,工具位姿为
>> two_link.fkine([pi/4 -pi/4])
ans =
1.0000 0 0 1.7071
0 1.0000 0 0.7071
0 0 1.0000 0
0 0 0 1.0000
按照惯例,机器人工具箱使用的关节坐标都是行向量。
用以下指令可以画出机器人的图形:
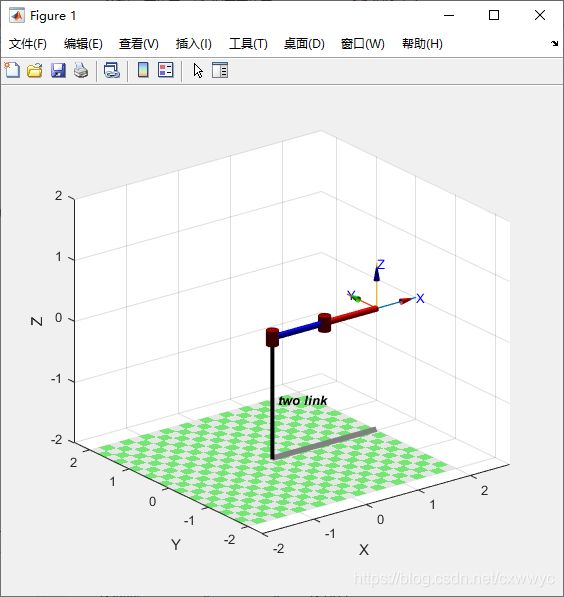
>> two_link.plot([0 0])
>> two_link.plot([pi/4 -pi/4])
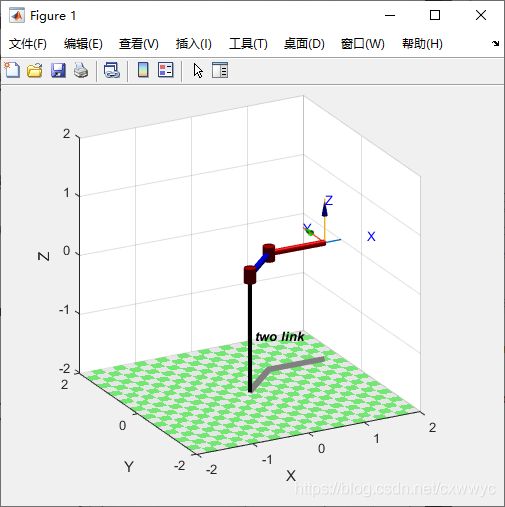
图中包含了机器人的名称,末端连杆的坐标系(此例的 T 2 T_2 T2),所有的关节和它们的轴线,以及机器人投影在地面上的影子。有关plot方法的更多特性,如多视图和多机器人绘制,之后有机会再介绍,更详细的说明参见在线文档。
上面介绍的简单两连杆机器人所能达到的姿态有限,因为它的运动完全在 x y xy xy 平面内,其任务空间是 J ⊂ R 2 \mathcal{J}\subset\mathbb{R}^2 J⊂R2。
六轴机器人
真正实用的机器人的任务空间是 J ⊂ S E ( 3 ) \mathcal{J}\subset SE(3) J⊂SE(3),这就使得其末端执行器能到达任意的位置和姿态。这个任务空间有 6 6 6 个空间自由度: 3 3 3 个平移和 3 3 3 个转动。这需要一个具有位形空间 C ⊂ R 6 \mathcal{C}\subset\mathbb{R}^6 C⊂R6 的机器人,即一个有 6 6 6 关节的机器人。本节中,我们将以 Puma560 机器人作为所有全旋转六轴机械臂的一个例子来介绍。我们使用如下指令来定义一个 Puma560 机器人的实例:
>> mdl_puma560
它将在工作区中创建一个名为p560的SerialLink对象:
>> p560
p560 =
Puma 560 (6 axis, RRRRRR, stdDH, fastRNE)
viscous friction; params of 8/95;
+---+-----------+-----------+-----------+-----------+-----------+
| j | theta | d | a | alpha | offset |
+---+-----------+-----------+-----------+-----------+-----------+
| 1| q1| 0| 0| 1.571| 0|
| 2| q2| 0| 0.4318| 0| 0|
| 3| q3| 0.15| 0.0203| -1.571| 0|
| 4| q4| 0.4318| 0| 1.571| 0|
| 5| q5| 0| 0| -1.571| 0|
| 6| q6| 0| 0| 0| 0|
+---+-----------+-----------+-----------+-----------+-----------+
grav = 0 base = 1 0 0 0 tool = 1 0 0 0
0 0 1 0 0 0 1 0 0
9.81 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1
请注意, a j a_j aj 和 d j d_j dj 都采用国际标准单位,这意味着正向运动学的平移部分也将使用国际标准单位。
指令“md1_puma560”还在工作区中创建了大量关节坐标向量,它们代表了一些典型的机器人位形:
qz |
( 0 , 0 , 0 , 0 , 0 , 0 ) (0, 0, 0, 0, 0, 0) (0,0,0,0,0,0) | 零角度 |
|---|---|---|
qr |
( 0 , π 2 , − π 2 , 0 , 0 , 0 ) (0, \dfrac{\pi}{2}, -\dfrac{\pi}{2}, 0, 0, 0) (0,2π,−2π,0,0,0) | 就绪状态,机械臂伸直且垂直 |
qs |
( 0 , 0 , − π 2 , 0 , 0 , 0 ) (0, 0, -\dfrac{\pi}{2}, 0, 0, 0) (0,0,−2π,0,0,0) | 伸展状态,机械臂伸直且水平 |
qn |
( 0 , π 4 , − π , 0 , π 4 , 0 ) (0, \dfrac{\pi}{4}, -\pi, 0, \dfrac{\pi}{4}, 0) (0,4π,−π,0,4π,0) | 标准状态,机械臂处于一个灵巧工作姿态(远离奇异点) |
使用plot方法绘制位形,例如
>> p560.plot(qz)
>> p560.fkine(qz)
ans =
1.0000 0 0 0.4521
0 1.0000 0 -0.1500
0 0 1.0000 0.4318
0 0 0 1.0000
它返回一个对应末端执行器位姿的齐次变换 T 6 T_6 T6。机器人上连杆 6 6 6 坐标系 { 6 } \{6\} {6} 的原点被定义为最后三个关节轴的交点——这个点在机器人的腕关节内部。通过如下的命令:
>> p560.tool = transl(0, 0, 0.2);
我们可以定义一个工具变换,从 T 6 T_6 T6 坐标系变换到实际的工具顶端。在本例中,工具顶端是沿着 T 6 T_6 T6 的 z z z 轴延伸了 200 m m 200mm 200mm。此时,工具顶端(也称工具中心点或者 TCP)的位姿变成
>> p560.fkine(qz)
ans =
1.0000 0 0 0.4521
0 1.0000 0 -0.1500
0 0 1.0000 0.6318
0 0 0 1.0000
我们在定义上述运动学变换时,认为机器人的基座点是位于机器人结构内部的腰关节和肩关节轴线的交点上。Puma560 机器人有一个 30 30 30 英寸高的底座结构。我们可以通过一个基座变换将机器人的原点从其内部转移到底座的下端部:
>> p560.base = transl(0, 0, 30*0.0254);
其中,为了一致,我们将底座高度转换为了国际标准单位。现在,经过基座变换和工具变换之后,正向运动学变为
>> p560.fkine(qz)
ans =
1.0000 0 0 0.4521
0 1.0000 0 -0.1500
0 0 1.0000 1.3938
0 0 0 1.0000
可以看到,现在工具的 z z z 坐标值比以前更大。
我们还可以做更多有趣的事情,例如:
>> p560.base = transl(0, 0, 3) * trotx(pi);
>> p560.fkine(qz)
ans =
1.0000 0 0 0.4521
0 -1.0000 -0.0000 0.1500
0 0.0000 -1.0000 2.3682
0 0 0 1.0000

它将机器人的坐标原点比世界坐标原点升高了 3 m 3m 3m,并让机器人坐标系绕着 x x x 轴旋转 180 ° 180° 180°。现在机器人就像挂在天花板上一样!(可能需要缩放后才能看得见)
机器人工具箱支持关节角按时间序列或按轨迹线的显示方式,例如,我们定义一个不同时间的关节坐标值:
>> q
q =
0 0 0 0 0 0
0 0.0365 -0.0365 0 0 0
0 0.2273 -0.2273 0 0 0
0 0.5779 -0.5779 0 0 0
0 0.9929 -0.9929 0 0 0
0 1.3435 -1.3435 0 0 0
0 1.5343 -1.5343 0 0 0
0 1.5708 -1.5708 0 0 0
其中每一行表示不同时间步下的关节坐标值,而每列的数字则对应每个关节。此时再使用方法fkine:
>> T = p560.fkine(q)
它将返回一个三维矩阵:
>> about(T)
T [double] : 4x4x8 (1.0 kB)
其中,前两维是一个 4 × 4 4×4 4×4 阶的齐次变换矩阵,第三维是time step。对应于q中第 4 4 4 行关节坐标值的齐次变换矩阵是
>> T(:,:,4)
ans =
1.0000 0.0000 0 0.3820
0 -1.0000 -0.0000 0.1500
0 0.0000 -1.0000 2.1323
0 0 0 1.0000
之后我们还会讨论如何创建一个轨迹。